7.2 Криволинейный интеграл второго рода
Пусть
векторная функция
определена
и непрерывна на некоторой кривой AB
в плоскости
.
Разобьем кривую AB произвольным образом на n частей точками
,
выберем на каждой
из частичных дуг
произвольную точку
(рис. 7.2) и составим сумму
,
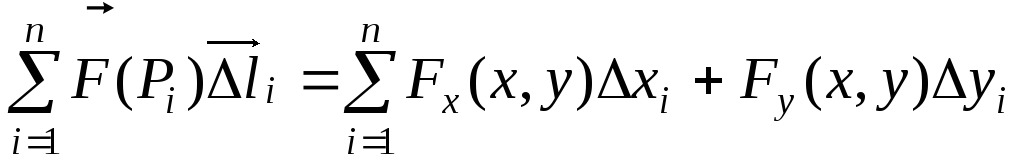где
.
Данная сумма называетсяинтегральной
суммой для
векторной функции
по кривой AB.
Обозначим через
наибольшую из длин частичных векторов
:
.
Рис. 7.2. Разбиение кривой AB на частичные дуги в случае
криволинейного интеграла второго рода
Определение.
Криволинейным
интегралом второго рода от
функции
по кривой AB
называется предел интегральных сумм
при
,
если этот предел существует и не зависит
ни от способа разбиения кривойAB
на частичные
дуги
,
ни от выбора в каждой из них точки
:
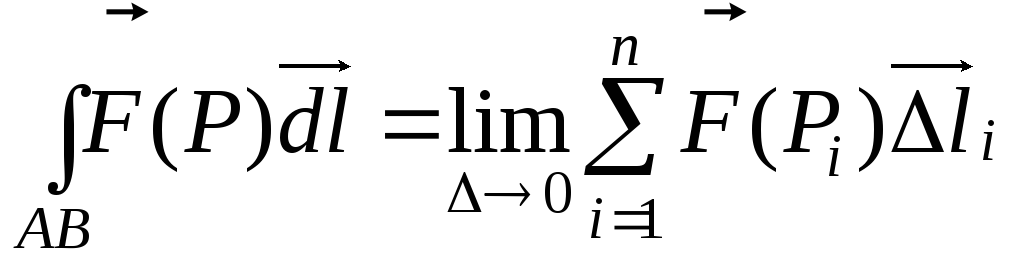
или в другой записи:
,
где векторный
элемент касательной
к контуру интегрирования в точке
равен
и скалярное произведение
.
Функция
называется интегрируемой
по (вдоль)
кривой AB,
сама кривая AB
– контуром
интегрирования,
A
– начальной, а B
– конечной точками интегрирования.
Если AB – замкнутая кривая, т.е. точка B совпадает с точкой A, из двух возможных направлений обхода замкнутого контура AB условимся называть положительным то направление, при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода контура AB условимся называть отрицательным.
Криволинейный
интеграл по замкнутому контуру
,
пробегаемому в положительном направлении,
обычно обозначают так:
.
Теорема
7.2 (существования криволинейного
интеграла второго рода) (без доказательства).
Функция
,
непрерывная вдоль кусочно-гладкой
кривой AB,
интегрируема по этой кривой.
Основные свойства криволинейного интеграла второго рода аналогичны соответствующим свойствам криволинейного интеграла первого рода, за исключением свойства 5:
При изменении направления интегрирования криволинейный интеграл второго рода изменяет знак:
.
Простейший
физический
смысл криволинейного интеграла второго
рода– работа
силового поля
при перемещении в нем материальной
точки по кривойAB
из точки A
в точку B.
Вычисление криволинейного интеграла второго рода сводится к вычислению определенных интегралов следующими способами.
Если кривая AB
задана параметрически уравнениями
,
то
.
Если кривая AB
задана явно уравнением
,
то
.
Если кривая AB
задана явно уравнением
,
то
.
Замечание. Для
пространственной кривой AB,
заданной параметрически уравнениями
,
формула для вычисления криволинейного
интеграла второго рода имеет вид
аналогичный
соответствующей формуле для плоской
кривой.
Пример. Вычислить криволинейный интеграл второго рода
,
где L
– замкнутый контур ABCA,
образованный прямыми
(рис. 7.3).
Разобьем контур интегрирования L на три части AB, BC, CA и вычислим исходный интеграл по каждому из этих участков, используя формулу для вычисления криволинейного интеграла второго рода в случае явно заданной кривой.
.
.
.
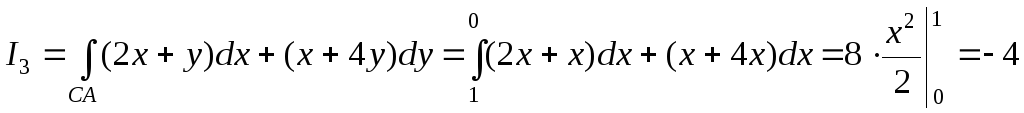Используя свойство 3 криволинейных интегралов, получаем
.
Рис. 7.3. Пример вычисления криволинейного интеграла второго рода