
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
Для тройных интегралов, как и для двойных, имеют место формулы замены переменных при переходе от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сферические координаты.
Переход от
прямоугольных координат
![]() кцилиндрическим
координатам
кцилиндрическим
координатам
![]() (рис. 6.8),
связанным с
(рис. 6.8),
связанным с
![]() соотношениями
соотношениями
![]() ,
,
осуществляется по формуле
![]() .
.
Выражение
![]() называют элементом объема в цилиндрических
координатах.
называют элементом объема в цилиндрических
координатах.
Название
«цилиндрические координаты» связано
с тем, что координатная поверхность
![]() (т.е. поверхность, все точки которой
имеют одну и ту же координатуr)
является цилиндром, прямолинейные
образующие которого параллельны оси
(т.е. поверхность, все точки которой
имеют одну и ту же координатуr)
является цилиндром, прямолинейные
образующие которого параллельны оси
![]() .
.
Рис. 6.8. Цилиндрические (слева) и сферические (справа) координаты
Переход от
прямоугольных координат
![]() ксферическим
координатам
ксферическим
координатам
![]() (рис. 6.8),
связанным с
(рис. 6.8),
связанным с
![]() соотношениями
соотношениями
![]() ,
,
осуществляется по формуле
![]() .
.
Выражение
![]() называют элементом объема в сферических
координатах.
называют элементом объема в сферических
координатах.
Название «сферические
координаты» связано с тем, что координатная
поверхность
![]() (т.е. поверхность, все точки которой
имеют одну и ту же координату
(т.е. поверхность, все точки которой
имеют одну и ту же координату![]() )
является сферой с центром в начале
координат.
)
является сферой с центром в начале
координат.
Пример. Вычислить тройной интеграл
![]() ,
,
где
![]() – область,
ограниченная поверхностями
– область,
ограниченная поверхностями
![]() и
и![]() (рис. 6.9).
(рис. 6.9).
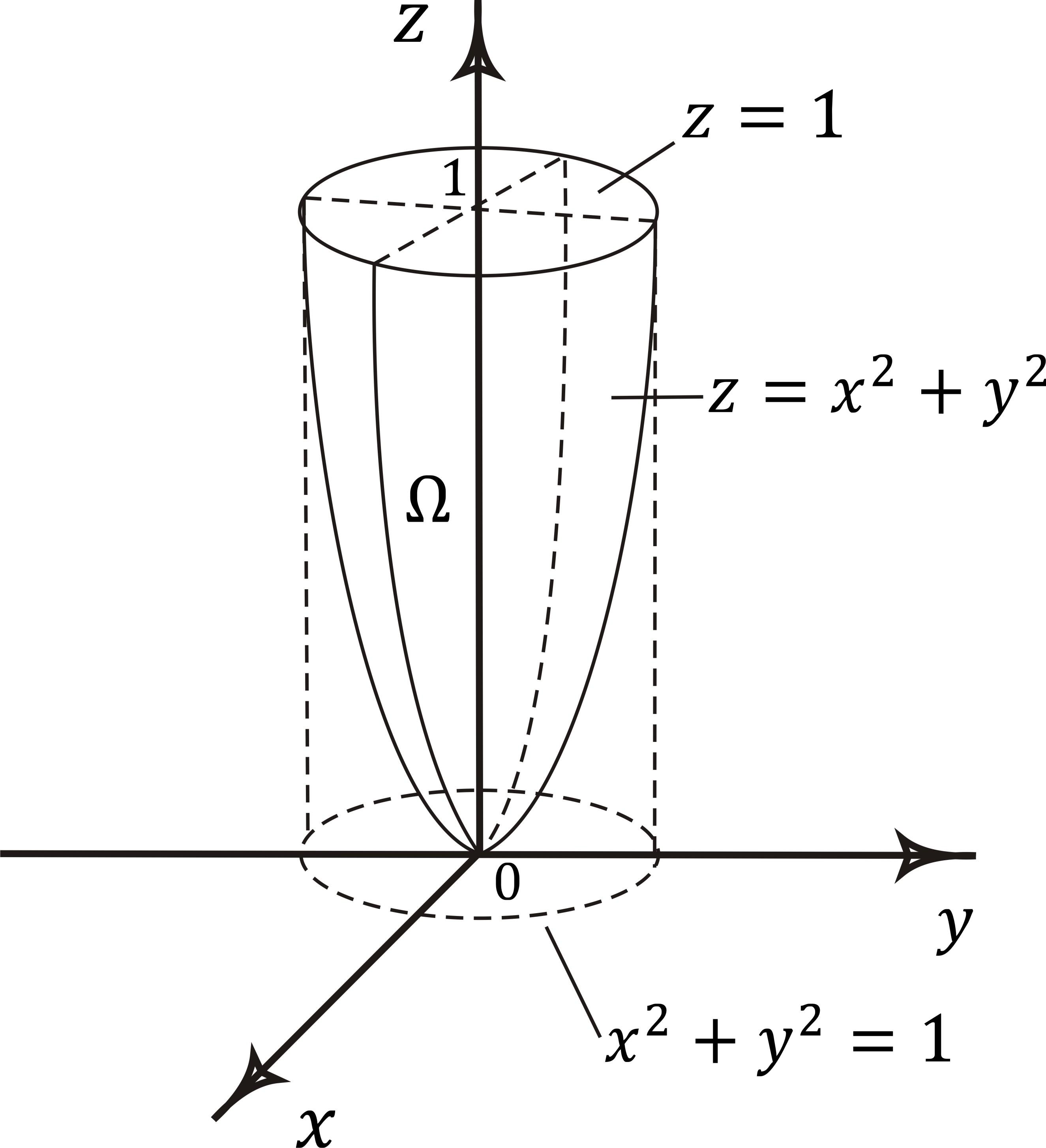
Рис. 6.9. Пример вычисления тройного интеграла в цилиндрических координатах
В данном примере удобно перейти от прямоугольных к цилиндрическим координатам.
Так как область
![]() проектируется на плоскость
проектируется на плоскость![]() в круг
в круг![]() ,
то угол
,
то угол![]() изменяется в пределах от 0 до
изменяется в пределах от 0 до![]() ,
радиус-векторr
изменяется
в пределах от 0 до 1. Координата z
изменяется от значений для точек, лежащих
на параболоиде
,
радиус-векторr
изменяется
в пределах от 0 до 1. Координата z
изменяется от значений для точек, лежащих
на параболоиде
![]() ,
до значений для точек, лежащих на
плоскости
,
до значений для точек, лежащих на
плоскости![]() ,
т.е.
,
т.е.![]() .
.
Применяя формулу для вычисления тройного интеграла в цилиндрических координатах, получаем

![]()
 .
.
7 Криволинейные интегралы
7.1 Криволинейный интеграл первого рода
Пусть функция
![]() определена и непрерывна на некоторой
кривойAB
в плоскости
определена и непрерывна на некоторой
кривойAB
в плоскости
![]() .
.
Разобьем кривую AB произвольным образом на n частей точками
![]() ,
,
выберем на каждой
из частичных дуг
![]() произвольную точку
произвольную точку![]() (рис. 7.1) и составим сумму
(рис. 7.1) и составим сумму
 ,
,
где
![]() – длина дуги
– длина дуги![]() .
Данная сумма называетсяинтегральной
суммой для
функции
.
Данная сумма называетсяинтегральной
суммой для
функции
![]() по кривойAB.
Обозначим через
по кривойAB.
Обозначим через
![]() наибольшую из длин частичных дуг
наибольшую из длин частичных дуг![]() :
:
![]() .
.

Рис. 7.1. Разбиение кривой AB на частичные дуги в случае
криволинейного интеграла первого рода
Определение.
Криволинейным
интегралом первого рода от
функции
![]() по кривойAB
называется предел интегральных сумм
при
по кривойAB
называется предел интегральных сумм
при
![]() ,
если этот предел существует и не зависит
ни от способа разбиения кривойAB
на частичные
дуги
,
если этот предел существует и не зависит
ни от способа разбиения кривойAB
на частичные
дуги
![]() ,
ни от выбора в каждой из них точки
,
ни от выбора в каждой из них точки![]() :
:

или в другой записи:
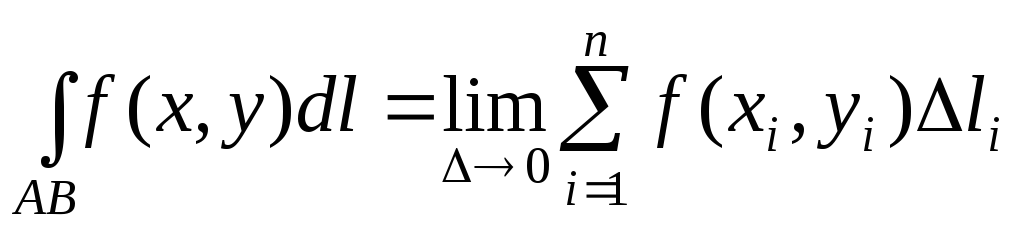 .
.
Функция
![]() называетсяинтегрируемой
по (вдоль)
кривой AB,
сама кривая AB
– контуром
интегрирования,
A
– начальной, а B
– конечной точками интегрирования.
называетсяинтегрируемой
по (вдоль)
кривой AB,
сама кривая AB
– контуром
интегрирования,
A
– начальной, а B
– конечной точками интегрирования.
Определение. Кривая, заданная параметрически уравнениями
![]() ,
,
называется гладкой,
если функции
![]() и
и![]() непрерывны и имеют непрерывные производные
непрерывны и имеют непрерывные производные![]() и
и![]() ,
не обращающиеся в нуль одновременно
(тем самым кривая в каждой точке имеет
касательную).
,
не обращающиеся в нуль одновременно
(тем самым кривая в каждой точке имеет
касательную).
Непрерывная кривая, составленная из конечного числа гладких кусков, называется кусочно-гладкой.
Кривая, заданная
явно уравнением
![]() ,
будет гладкой, если функция
,
будет гладкой, если функция![]() и ее производная
и ее производная![]() непрерывны на отрезке
непрерывны на отрезке![]() .
.
Теорема
7.1 (существования криволинейного
интеграла первого рода) (без доказательства).
Функция
![]() ,
непрерывная вдоль кусочно-гладкой
кривойAB,
интегрируема по этой кривой.
,
непрерывная вдоль кусочно-гладкой
кривойAB,
интегрируема по этой кривой.
Замечание.
Если положить
![]() всюду на кривойAB,
то из определения криволинейного
интеграла первого рода легко получить
формулу для вычисления длины дуги l
кривой AB
с помощью криволинейного интеграла
первого рода:
всюду на кривойAB,
то из определения криволинейного
интеграла первого рода легко получить
формулу для вычисления длины дуги l
кривой AB
с помощью криволинейного интеграла
первого рода:

или
![]() .
.
Основные свойства криволинейного интеграла первого рода аналогичны соответствующим свойствам определенного интеграла.
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
![]() .
.
Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
![]() .
.
Свойство 3. Если кривую AB разбить на две кривые AC и CB, то интеграл по всей кривой AB будет равен сумме интегралов по кривым AC и CB:
![]() .
.
Свойство 4
(Теорема о среднем).
Если функция
![]() непрерывна вдоль гладкой кривойAB,
то на этой кривой существует такая точка
непрерывна вдоль гладкой кривойAB,
то на этой кривой существует такая точка
![]() ,
что справедлива формула
,
что справедлива формула
 ,
,
где l – длина кривой AB.
Свойство 5. При изменении направления интегрирования величина интеграла не изменяется:
![]() .
.
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла следующими способами.
Если кривая AB
задана параметрически уравнениями
![]() ,
то
,
то
 .
.
Если кривая AB
задана явно уравнением
![]() ,
то
,
то
 .
.
Если кривая AB
задана явно уравнением
![]() ,
то
,
то
 .
.
Замечание. Для
пространственной кривой AB,
заданной параметрически уравнениями
![]() ,
формула для вычисления криволинейного
интеграла первого рода имеет вид
,
формула для вычисления криволинейного
интеграла первого рода имеет вид
 ,
,
аналогичный соответствующей формуле для плоской кривой.
Пример. Вычислить криволинейный интеграл первого рода
![]() ,
,
где AB
– отрезок
прямой
![]() от точки
от точки![]() до
точки
до
точки![]() .
.
Имеем
![]() .
.
По формуле вычисления криволинейного интеграла первого рода получаем
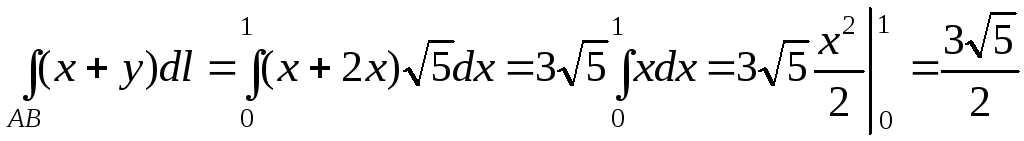 .
.
