
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
4.8 Уравнения высшего порядка, допускающие понижение порядка
1) Уравнение вида .
Метод решения. Общее решение уравнения находится n-кратным интегрированием (последовательным взятием квадратур).
Пример. Найти общее решение уравнения
![]() .
.
Последовательно интегрируя почленно исходное уравнение три раза (беря квадратуры), находим общее решение:
![]() ,
,
![]() ,
,
![]() .
.
2) Уравнение вида .
Метод решения.
Уравнение не содержит явно искомой
функции y
и ее производных
до порядка
![]() включительно, поэтому с помощью
подстановки
включительно, поэтому с помощью
подстановки![]() порядок уравнения понижается наk
единиц:
порядок уравнения понижается наk
единиц:
![]() ,
,
так как
![]() .
.
Если для вновь полученного уравнения можно найти общее решение
![]() ,
,
то общее решение исходного уравнения получается путем k-кратного интегрирования функции
![]() .
.
В частности, если
уравнение 2-го порядка не содержит y,
то замена переменных
![]() приводит к уравнению 1-го порядка.
приводит к уравнению 1-го порядка.
Пример. Найти общее решение дифференциального уравнения
![]() .
.
Так
как исходное уравнение не содержит
![]() и
и![]() ,
то сделаем подстановку
,
то сделаем подстановку
![]() .
Тогда
.
Тогда![]() и из исходного уравнения 3-го порядка
получаем уравнение 1-го порядка
и из исходного уравнения 3-го порядка
получаем уравнение 1-го порядка
![]() ,
,
которое является
уравнением с разделяющимися переменными
![]() .
Находим его общее решение
.
Находим его общее решение

 .
.
Теперь найдем общее решение исходного уравнения путем двукратного интегрирования функции
![]() .
.
Получаем:
![]()
 .
.
3) Уравнение вида .
Метод решения.
Уравнение не содержит явно независимой
переменной x,
поэтому с
помощью подстановки
![]() порядок уравнения понижается на
единицу:
порядок уравнения понижается на
единицу:
 ,
,
так как производные
![]() выражаются при этом через производные
порядка не выше
выражаются при этом через производные
порядка не выше![]() отp
по y.
Действительно, по правилу дифференцирования
сложной функции получаем
отp
по y.
Действительно, по правилу дифференцирования
сложной функции получаем
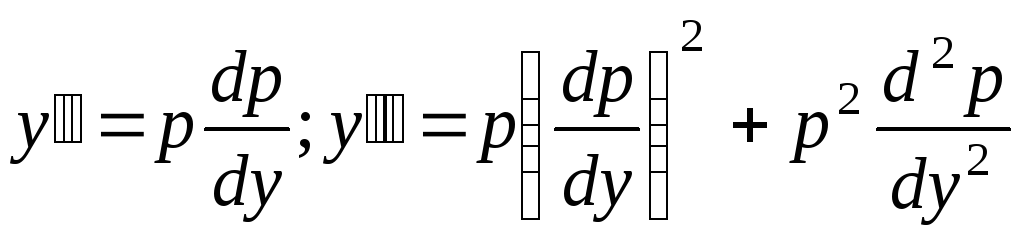 и т.д.
и т.д.
Пример. Найти общее решение дифференциального уравнения
![]() .
.
Так как исходное
уравнение не содержит явно независимой
переменной x,
то
сделаем подстановку
![]() .
Тогда
.
Тогда
 и из исходного уравнения 2-го порядка
получаем уравнение 1-го порядка
и из исходного уравнения 2-го порядка
получаем уравнение 1-го порядка
 ,
,
которое является
уравнением с разделяющимися переменными
![]() .
Находим его общее решение:
.
Находим его общее решение:
 ;
;
![]()

 .
.
Теперь найдем общее решение исходного уравнения:
![]()
![]()
![]() ;
;

4.9 Линейные дифференциальные уравнения высшего порядка
Определение. Линейным
дифференциальным уравнением высшего
(n-го)
порядка называется
уравнение, линейное относительно
неизвестной функции
![]() и ее производных
и ее производных
![]() .
.
Функции
![]() называютсякоэффициентами
уравнения.
Функция
называютсякоэффициентами
уравнения.
Функция
![]() называетсяправой
частью уравнения.
называетсяправой
частью уравнения.
Если
![]() ,
то уравнение называетсялинейным
однородным уравнением
или уравнением
без правой части.
,
то уравнение называетсялинейным
однородным уравнением
или уравнением
без правой части.
Если
же
![]() ,
то уравнение называетсялинейным
неоднородным уравнением
или уравнением
с правой частью.
,
то уравнение называетсялинейным
неоднородным уравнением
или уравнением
с правой частью.
Примеры
![]() –линейное однородное
уравнение 3-го порядка.
–линейное однородное
уравнение 3-го порядка.
![]() –линейное неоднородное
уравнение 2-го порядка.
–линейное неоднородное
уравнение 2-го порядка.
Из определения линейного однородного уравнения и свойств линейности производных следует очевидное свойство решений линейного однородного уравнения: линейная комбинация решений линейного однородного уравнения является решением того же уравнения.
Из определения
линейного неоднородного уравнения и
свойств линейности производных следует
очевидное свойство
решений линейного неоднородного
уравнения:
сумма решений линейного неоднородного
уравнения и соответствующего (![]() )
однородного уравнения
является решением неоднородного
уравнения.
)
однородного уравнения
является решением неоднородного
уравнения.
Выясним структуру общих решений линейного однородного уравнения и линейного неоднородного уравнения.
Теорема
4.3 (без доказательства).
Общим решением на отрезке
![]() линейного однородного уравнения
линейного однородного уравнения
![]()
с непрерывными на
отрезке
![]() коэффициентами
коэффициентами
![]() является линейная комбинация
является линейная комбинация
![]()
n
линейно
независимых на том же отрезке частных
решений этого уравнения
![]() .
.
Теорема
4.4 (без доказательства).
Общее решение на отрезке
![]() линейного неоднородного уравнения
линейного неоднородного уравнения
![]()
с непрерывными на
отрезке
![]() коэффициентами
коэффициентами
![]() и непрерывной правой частью
и непрерывной правой частью![]() равно сумме общего решения
равно сумме общего решения
![]()
соответствующего однородного уравнения
![]()
и какого-нибудь
частного решения
![]() неоднородного уравнения:
неоднородного уравнения:
![]() .
.
