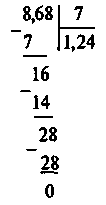Плани-конспекти математика 5 клас / urok_101

2.3. Множення і ділення десяткових дробів

Урок №101

Тема. Ділення десяткових дробів.

Мета: встановити правило ділення десяткового дробу на натуральне число; формувати вміння застосовувати це правило в різних ситуаціях ділення десяткового дробу на натуральне число.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Актуалізація опорних знань

Запитання до класу

1. Як називається числа а, b і с у запису a : b = c?

2. Як перевірити правильність рівності а : b = с?

3. Як знайти невідомий множник?

4. Як знайти невідоме ділене?

5. Як знайти невідомий дільник?

6. Як дізнатись, у скільки разів число а більше за число b?

7. Чому дорівнює частка: а : 1; а : а; 0 : а?

8. Обчисли: 0,3 · 4; 0,5 · 5; 0,5 · 2.

9. Знайди серед чисел пари рівних: 3,1; 3,01; 3,10; 1,05; 1,5; 10,5; 1,050.

II. Формування знань

Учитель пропонує учням розв'язати завдання.

1. Як знайти невідомий множник у рівнянні 4х = 1,2 ? Чи є коренем цього рівняння число 0,3? 3,30?

(Невідомий множник дорівнює частці від ділення добутку на відомий множник: х = 1,2 : 4, зрозуміло, що х = 0,3, бо 4 · 0,3 = 1,2.)

2. Як знайти невідомий дільник у рівнянні 2,5 : х = 5? Чи є коренем цього рівняння число 5; 0,5; 0,05?

(Невідомий дільник дорівнює частці від ділення діленого на частку:

х= 2,5:5, зрозуміло, що корінь х = 0,5, бо 0,5 · 5 = 2,5).

Учні разом з учителем доходять висновку:

1,2 : 4 = 0,3; 2,5 : 5 = 0,5.

Після чого переходять до розбору першого прикладу в підручнику (від ділення десяткового дробу на натуральне число «куточком» маємо:

4352 : 17 = 256, 43,52 : 17 = 2,56,

бо

Отже, можна сказати, що при діленні десяткового дробу на натураль­не число (кутком) можна:

1. ділити дріб на натуральне число, не звертаючи уваги на кому;

2. після закінчення ділення цілої частини діленого треба в частці поста­вити кому.

Після цього учні розбирають і записують у зошитах розв'язання кількох прикладів на ділення за складеною вище схемою.

Приклад 1. 8,68 : 7 = 4.

Приклад 2. 169,6 : 8 = 21,2.

Після засвоєння загального правила розглядаються особливі випадки (ціла частина діленого менша від дільника або дорівнює 0; цифри діленого закінчилися, а 0 в остачі не отримано; натуральне число ділиться на нату­ральне).

Приклад 3.

Приклад 4.

Приклад 5.

Висновок. У будь-якому разі ділення десяткового дробу на натуральне число виконується майже так, як ділення натуральних чисел. Відміна лише в тому, що в частці треба на певному місці поставити кому і можна дописати нулі справа у дробовій частині.

III. Закріплення знань. Формування вмінь

Для кращого засвоєння алгоритму ділення десяткового дробу на нату­ральне число на уроці розв'язують лише вправи початкового і середнього рівня складності і кожний випадок ділення коментується. ^Зч На цьому ж уроці можна запропонувати учням розв'язати приклади на сумісні арифметичні дії з десятковими дробами та рівняння, розв'я­зання яких передбачає ділення десяткового дробу на натуральне число. Розв'язування вправ №№ 928; 929 (непарні); 931; 934 (1-3); 947.

IV. Підсумок уроку

Наприкінці уроку вчитель разом з учнями повторює алгоритм вико­нання дії ділення десяткового дробу на натуральне число і акцентує увагу учнів на тому факті, що ця дія, так само, як і додавання, віднімання і мно­ження десяткових дробів, зводиться, фактично, до однойменних дій, але з натуральними числами.

V. Домашнє завдання

п. 32, №№ 930; 935 (1-3); 948.

2

С.П.Бабенко УРОКИ МАТЕМАТИКИ 5 клас Урок 101