Плани-конспекти математика 5 клас / urok_66

2.1. Звичайні дроби

УРОК № 66

Тема. Уявлення про звичайні дроби.

Мета: закріпити знання учнів щодо читання, запису звичайних дробів та розв'язування задач на знаходження дробу від числа, а також доповнити ці знання алгоритмом розв'язання задачі на знаходження числа за його дробом.

Тип уроку: засвоєння знань, умінь, навичок.

Хід уроку

І. Перевірка домашнього завдання

Письмову частину домашнього завдання вчитель перевіряє лише у слабких учнів, зібравши їхні зошити перед уроком. На уроці перевіря­ються засвоєння теоретичних знань та способів дій. Учням пропонується виконати усні вправи.

1. Прочитайте дроби, назвіть у кожному з них чисельник і знаменник:

1) ; 2) ; 3) ; 4) ; 5) .

2. Наведіть приклад дробу:

1) знаменник якого на 5 більший за чисельник;

2) чисельник якого втричі менший від знаменника.

3. Петрик пофарбував паркан за 4 год. Яку частину паркану він пофар­бував за 3 год?

4. Сад прямокутної форми має довжину 40 м, ширину 30 м. Вишні зай­мають саду. Скільки арів засаджено вишнями?

5. Порівняйте:

1) дм і 5 см; 2) год і 18 хв; 3) т і 695 кг; 4) прямого кута і 49°.

II. Актуалізація опорних знань

Здійснюється під час виконання учнями усних вправ, якщо вчитель вимагає від них робити пояснення.

III. Доповнення знань

1. Відомо, що однієї банки фарби вистачає, щоб пофарбувати 100 м² підлоги. Яка частина фарби залишиться після того, як пофарбують підлогу в кабінеті шириною 5 м і довжиною 8 м?

2. Пофарбувавши 10 м² підлоги, з'ясували, що витрачено 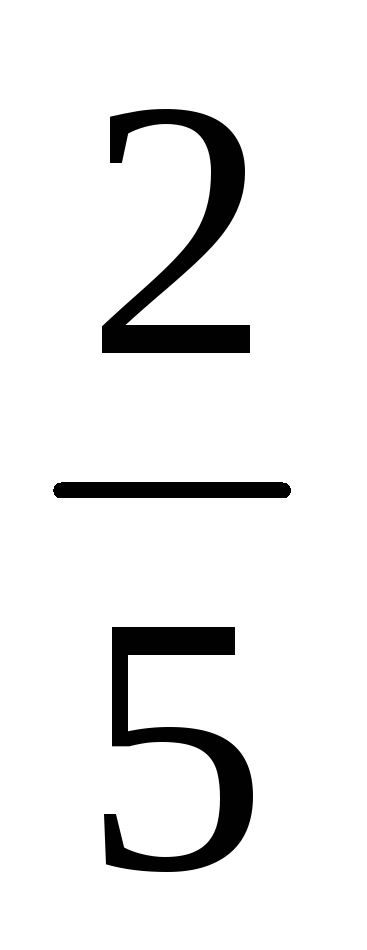банки фарби. Чи вистачить цього, щоб пофарбувати підлогу, якщо кімната має розміри 5 м х 8 м?

[Розв'язання. 1) 10 : 2 = 5 (м²) — на скільки вистачить банки;

5 · 5 = 25 (м²) — на скільки вистачить усієї банки;

5 · 8 = 40 (м²) — площа підлоги;

25 < 40, отже, не вистачить.]

Після розв'язання задач учитель наголошує, що поняття звичайних дробів допомагає розв'язувати як задачі на знаходження якоїсь частини (дробу) від даного числа, так і обернені задачі (за дробом знайти число), розбираються задачі № 2, 3, що розв'язані в п. 22 підручника.

IV. Закріплення знань. Розв'язування вправ

1. Найпростіші задачі на знаходження числа за його дробом № 666, 668.

2. № 675, 679 — арифметичні задачі на знаходження дробу від числа.

3. № 685 — задачі на рух із застосуванням алгоритму знаходження числа за його дробом.

4. № 687 — комбінована задача (знайти дріб від числа і потім число за його дробом).

Додаткові (логічні) вправи

1. Я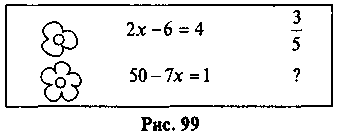ке з поданих чисел треба вибрати? (рис. 98)

2. Знайти пропущене число (рис. 99)

V. Домашнє завдання

п. 222, № 667; 669; 676; 678; 686; на повторення № 691 (2).

2

С.П.Бабенко УРОКИ МАТЕМАТИКИ 5 клас Урок 66