Плани-конспекти математика 5 клас / urok_31

1.3. Рівняння. Кути. Трикутники

УРОК № 31

Тема. Кут. Позначення кутів.

Мета: формувати поняття «кут», «вершина», «сторони кута», «бісек­триса кута», знайомство з позначенням кутів; формувати в учнів вміння будувати кут; розрізняти кути на готових рисунках і позначати кути різни­ми способами.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця-схема «Кути. Вимірювання кутів».

Хід уроку

I. Актуалізація опорних знань

Усні вправи

1. Назвіть усі промені, які ви бачите на рис. 23. Назвіть пари променів, що мають спільний початок.

2. Які з променів на рис. 24 перетинають промені АВ і АС?

3. Чому дорівнює довжина однієї ланки ламаної, яка складається з 16 рівних ла­нок і має довжину 90 см?

4. Щоб зробити огорожу для свого городу квадратної форми, Оленка відрізала 4 шматки дроту. Як перевірити, що ці 4 шматки підійдуть дівчинці (будуть рівними)?

II. Формування нових знань

План викладу навчального матеріалу

1. Поняття кута

2. Елементи кута

3. Позначення кутів

4. Поняття променя, що проходить між сторонами кута

5. Поняття рівних кутів

6. Поняття бісектриси кута

1-3. Пояснення вчитель супроводжує побудовою кута і в зошитах, і на дошці, учні роблять такі записи.

П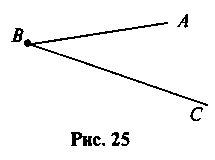ромені ВА і ВС виходять з точки В.

Тоді ABC — кут, ВА і ВС — сторони, В — вершина кута.

Кут позначається CBA або ABC, або В.

(Бажано літеру В виділити контрастним кольором.)

На закріплення цього матеріалу усно ви­конуються вправи.

1) Яке з позначень кута на рис. 26 є правиль­ним?

a) DBC; б) CDB; в) BCD; г) C.

2) Яка з фігур на рис. 27 зайва?

4. Поняття променя, що проходить між сторонами кута

 Поняття променя, що проходить між сторонами кута не дається стро­го (як у 7 класі), але бажано пояснити учням, що повинно виконуватися 2 умови: промінь виходить з вершини кута, проходить між сторонами, тобто будь-який відрізок з кінцями на сторонах кута буде перетнутий цим променем.

На закріплення поняття усно виконуються вправи.

На якому з рисунків промінь не проходить між сторонами кута АСВ?

(рис. 28)

5-6. На закріплення поняття рівних кутів і бісектриси кута — практичне завдання. Вчитель заздалегідь готує паперові моделі кутів (рис. 29).

Завдання 1. Як на моделі кута 1) побудувати бісектрису кута? [Перегнути так, щоб утворились два кути, що суміщаються, лінія перегину — бісектриса.]

Завдання 2. Як кут 2) розділити на 4 рівних частини? [Перегнути так, як у завданні 1, а потім утворений ще раз так само перегнути.]

Завдання 3. На моделі 3) проведено 2 промені так, що, перегнувши кути по цих променях, отримаємо 3 кути, що співпадають у разі накладан­ня. Чи можна промені, позначені на моделі, назвати бісектрисами даного кута? Чому? Чи є вони бісектрисами якихось інших кутів?

III. Закріплення матеріалу

Далі за підручником розв'язуємо задачі.

1. №№ 297; 299; 301— на закріплення нового матеріалу;

2. №№ 307; 308; 293 - на повторення.

Додатково: логічна вправа. Назвіть пропущене число і рисунок.

	3
	6	9
	9	9

IV. Підсумок уроку

Відповідаючи на запитання № 296, учні ще раз називають основні по­няття, розглянуті на уроці.

V. Домашнє завдання

п. 11, № 296 (усно); 298; 300; 302.

3

С.П.Бабенко УРОКИ МАТЕМАТИКИ 5 клас Урок 31