Плани-конспекти математика 6 клас / urok_76

V. Раціональні числа і дії над ними Тема 6. Раціональні числа. Порівняння, додавання і віднімання раціональних чисел

Урок № 76

Тема. Віднімання раціональних чисел.

Мета: сформувати уявлення учнів про зміст дії віднімання раціо­нальних чисел; а також виробити вміння застосовувати це правило для розв'язування вправ, що передбачають виконання раціональних чисел.

Тип уроку: засвоєння знань, умінь, навичок.

Хід уроку

І. Перевірка домашнього завдання

 Збираємо зошити на перевірку, виконавши попередньо невелику самостійну роботу на використання властивостей додавання і правил додавання раціональних чисел.

Варіант 1	Варіант 2
1. Виконайте додавання:
а) -379 + 948; б) -12 + (-8); в) -0,81 + 0,66; г) -5 + .	а) -35 + (-24); б) -543 + 458; в) 0,54 + (-0,83); г) .
2. Знайдіть значення виразу найзручнішим способом:
а) +3,2+(+8,42)+(-3,2)+(-6,4)+(-8,42); б)	а) -2,8+(+3,75)+(+2,8)+(-16,24)+(-3,75); б)

II. Актуалізація опорних знань

Запитання до класу

1. Як називають числа а, b і с у запису а – b = с?

2. Що означає від числа а відняти число b? (а - b означає знайти таке с, що с + а = b.)

3. Чому дорівнює різниця 11 – 8? Як перевірити результат? (11 – 8 = 3, бо 3 + 8 = 11.)

4. Назвіть число, протилежне від'ємнику в різницях: 3 – 4; 5 – 6; 7 – (-8); -7 – (-8); а – b; а – (-b).

III. Формування знань

 Основна думка, яку треба донести до свідомості учнів, що відніман­ня раціональних чисел ми можемо замінювати додаванням, а тому єдине, що треба з'ясувати — це спосіб, за допомогою якого ми змо­жемо замінити віднімання додаванням (маємо на увазі, що дода­вання раціональних чисел ми вже вміємо виконувати). Як і на по­передніх уроках (тема «Додавання раціональних чисел»), під час, «виведення» правила віднімання ми спочатку розглядаємо при­клад, що передбачає виконання віднімання раціональних чисел, а потім вже, знаючи властивості додавання, з'ясовуємо правило, за яким віднімання можна замінити додаванням.

Задача. Знайдіть х =-7 - (-4).

Розв'язання. Як відомо з попередніх класів, а – b = с, якщо b + с = а. Треба знайти х = -7 - (-4), тому -7 = -4 + х, але ж неважко здогадатись, що х = -3 (-4 + (-3) = -7). Спробуємо обчислити це, використовуючи інший спосіб: -7 - (-4) = -3 або ж -7 + 4 = -3.

Висновок 1. Щоб відняти число, треба до зменшуваного додати чис­ло, що протилежне від'ємнику, тобто a – b = a +(-b).

Наприклад

1) -10 + (+9) = -10 + (-9) = - (10 + 9) = -19;

2) 8 - (-5) = 8 + 5 але 3) 10,5 - 9 = 1,5.

(Правило заміни віднімання додаванням застосовувати не треба!)

Висновок 2. Правило a – b = a + (-b) використовуємо лише тоді, коли віднімання безпосередньо, як це робили в попередніх класах, не вико­нується.

IV. Закріплення знань. Засвоєння вмінь

Усні вправи

1. Прочитайте рівності і поясніть зміст перетворень:

-2 - 3 = -2 + (-3) = -5;

2 - 3 = 2 + (-3) = - (3 - 2) = - 1;

- 2 - (-3) = - 2 + 3 = 3 – 2 = 1.

Чи правильні рівності?

2. Замініть віднімання додаванням (до зменшуваного протилежного від'ємнику числа).

а - 3, b - (-3); с - 5; d - (-5); b - (-3); 8 - (-16): -6 - (-3); -b - (-10); -6 - 3; -8- 10.

Письмові вправи

1. Знайдіть різницю:

а) 278 - 78; б) 278 - (-78); в) -278 - 78; г) -278 - 278;

д) 7,2 - (7,2); є) 7,2 - 7,2; ж) -7,2 - (7,2); з) -7,2 - 2,7;

к) 0 - (-7,2); л) 0 - 7,2; м) -7,2 - 0; н) -7,2 - 7,2.

2. Розв'яжіть рівняння і виконайте перевірку:

а) -2 + х = 4,3; б) 8,1 + y = -6; в) 5 – х =1,7; г) 4 - y = -2;

д) z + = - ; e) z + 0,4 = -l.

3. *. Яке число більше і на скільки?

Перше число	0	-8,7	4	1	3,03	0
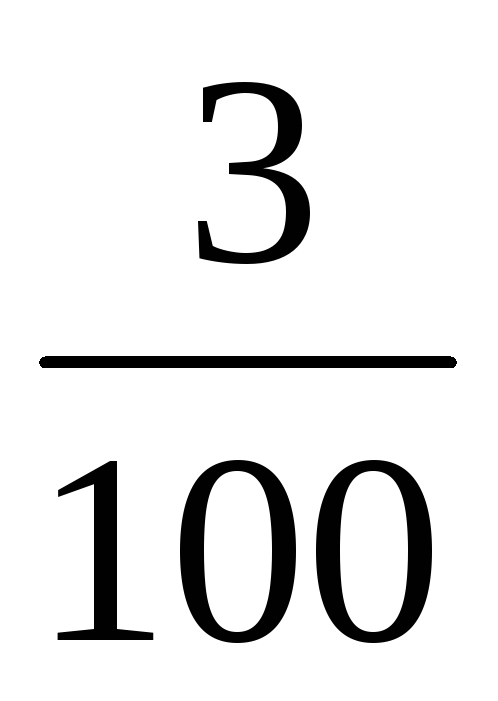
Друге число	-10	13	-8	2	3	705,9

4. Заповніть порожні клітинки таблиці:

Сума	-0,85	21	87	32,5
1 -й доданок		-17		34
2-й доданок	9,2		301

Додаткові вправи

5. Знайдіть пропущений рисунок:

		а – b
		2а – b

V. Підсумки уроку

Тестове запитання

Яке з поданих чисел дорівнює різниці р - k (див. рис):

1) -8; 2) 8; 3) -2; 4) 2.

VI. Домашнє завдання

1. Виконайте дії, замінивши, де потрібно, віднімання додаванням:

а) 26 - (-5); б) -4 + (-18); в) 14 - (-18); г) 10 - 7;

д) 4,7 - 8,1; є) -3,3 + 9,6; ж) 7 - (-4,9); з) -5 - (-2,9);

к) ; л) ; м) ; н)

о) - 0,7; п) -- (-0,4).

Задача. Для учнів було куплено 70 квитків у ляльковий театр. У пар­тер куплено квитків у 1,5 раза більше, ніж на балкон і бельетаж разом. Число квитків на балкон становило 0,4 від числа квитків на бельетаж. Скільки квитків кожного виду було куплено? Складіть рівняння.

3

С.П.Бабенко. Уроки математики 6 клас