
Плани-конспекти математика 6 клас / urok_17
.docІІ. Звичайні дроби Тема 2. Додавання і віднімання дробових чисел.
Урок № 17
Тема. Додавання і віднімання дробів з різними знаменниками
Мета: на основі вмінь додавати й віднімати дроби з однаковими знаменниками та зводити дроби до НСЗ, сформувати уявлення про алгоритм додавання і віднімання дробів з різними знаменниками, розпочати роботу з формування вмінь використовувати названі алгоритми (у найпростіших випадках)
Тип уроку: засвоєння нових знань
Хід уроку
I. Перевірка домашнього завдання
Зошити збираються на перевірку
II. Актуалізація опорних знань
Якщо на попередніх уроках була проведена відповідна робота (див урок 15, 14), а також були добре відпрацьовані навички зведення дробів до НСЗ, сприйняття алгоритму додавання і віднімання дробів з різними знаменниками не буде викликати труднощів у учнів Тому під час усної лічби достатньо ще раз розв'язати типові пропедевтичні завдання
Усні вправи
-
Обчисліть а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д)
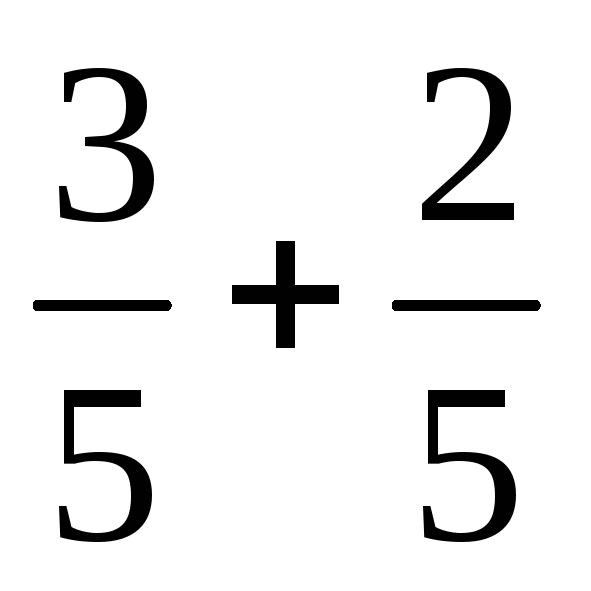 ;
е)
;
е)
 ;
;
ж)
![]() ;
з)
;
з)
![]() .
.
-
Скоротіть дріб:
 ;
;
 ;
;
 ;
;
 ;
;
 .
. -
Знайдіть НСЗ для дробів:
 і
і
 ;
;
 і
і
 ;
;
 і
і
 ;
;
 і
і
 .
. -
Якщо ціле поділено на 12 рівних частин, яким числом позначається одна така частина, дві; три частини?
-
На скільки
 більше за
більше за
 ?
Яку частину цілого становить разом
?
Яку частину цілого становить разом
 і
і
 частини цілого?
частини цілого?
III. Формування нових знань
Викладення нового матеріалу вчитель робить на свій розсуд або за підручником, або пропонує учням самостійно опрацювати розділ.
Якщо підготовка учнів достатня, то під час обговорення (це можна запропонувати у формі роботи в групах) розв'язання задач учні доходять висновку, як знайти суму (різницю) дробів з різними знаменниками. По завершенні цієї роботи можна записати конспект 11.
|
Конспект 11
Додавання
і віднімання дробів з різними
знаменниками:
1) Знайти НСЗ (НСК(b, d)). 2) Виконати додавання / віднімання дробів з однаковими знаменниками. 3) Якщо сума / різниця — скоротний дріб — скоротити. 4) Якщо сума / різниця — неправильний дріб, то виділити цілу частину. Приклад: 1)
2)
3)
|
П. 3) і 4) конспекту краще записати після розв'язування прикладу!).
IV. Формування вмінь
На цьому уроці тільки розпочинається робота з формування вмінь додавати і віднімати дроби з різними знаменниками, тому бажано на урок підібрати різноманітні завдання (приклади на «+» і «-», рівняння, найпростіші задачі), що передбачають додавання і віднімання правильних дробів. Також учителю слід звернути увагу на необхідність дотримання певних форм запису (див. конспект).
Розв'язування вправ
І рівень (усно)
-
Обчисліть:
 ;
;
 .
. -
Знайдіть НСЗ для дробів:
 і
і
 ;
;
 і
і
 ;
;
 і
і
 ;
;
 і
і
 ;
;
 і
і
 ;
;
 і
і
 ;
;
![]() і
і
![]() ;
;
![]() і
і
![]() .
.
II рівень (письмові вправи)
-
Обчисліть: а)
 +
+
 ;
б)
;
б)
 +
+
 ;
в)
;
в)
 +
+
 ;
г)
;
г)
 +
+
 .
. -
Замініть десятковий дріб звичайним і виконайте дії: а) 0,3 +
 ;
б) 0,25 +
;
б) 0,25 +
 ;
в) 0,36 –
;
в) 0,36 –
 ;
г)
;
г)
 – 0,45.
– 0,45. -
Знайдіть пропущені числа.

-
Знайдіть значення виразу: а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
Знайдіть значення виразу: а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
Розв'яжіть рівняння: а)
 ;
б)
;
б)
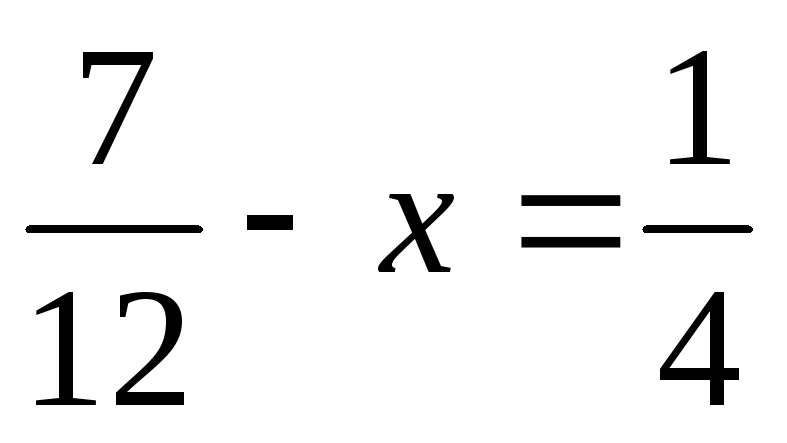 ;
в)
;
в)
 .
. -
Маса однієї деталі
 кг, а другої — на
кг, а другої — на
 кг менше. Знайдіть масу другої деталі.
кг менше. Знайдіть масу другої деталі. -
За перший день заасфальтували
 км дороги, за другий — на
км дороги, за другий — на
 кг менше. Скільки кілометрів дороги
заасфальтували за два дні?
кг менше. Скільки кілометрів дороги
заасфальтували за два дні?
Додаткові вправи
-
Замість * поставте знаки «+» і «-», щоб рівності стали правильними:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
-
Використовуючи кожну з цифр 1, 2, 3, 4 по одному разу, складіть такі дроби, щоб їх сума була
 .
.
V. Підсумки уроку
Чи правильно виконано додавання (віднімання) дробів?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Усі «неправильні» варіанти слід обговорити.
VI. Домашнє завдання
-
Обчисліть: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
. -
Знайдіть значення виразу: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д)
0,25 +
;
д)
0,25 +
![]() ;
е)
;
е)
![]() .
.
-
Розв'яжіть рівняння: а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
Площа однієї ділянки
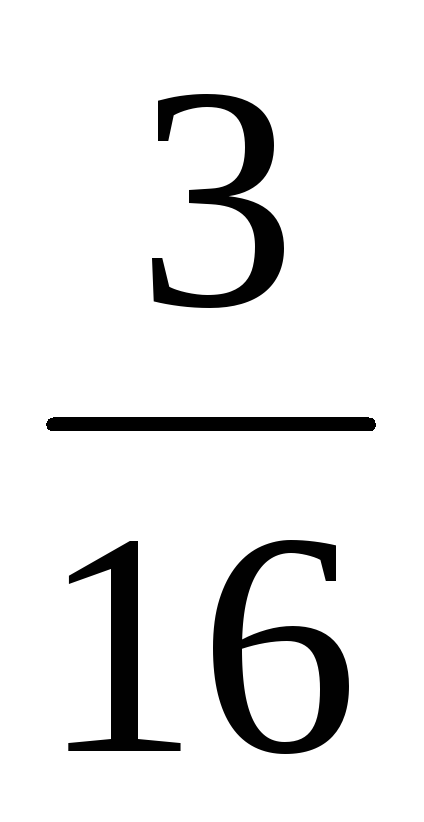 га, а другої — на
га, а другої — на
 га більше. Знайдіть площу другої ділянки.
га більше. Знайдіть площу другої ділянки. -
Запишіть десятковим дробом:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
