информатика_книги / Информатика. Теория и практика_Острейковский В.А, Полякова И.В_2008 -608с

Ðèñ. 7.27. График функции f(x) = – 4 после редактирования осей координат

x

Ðèñ 7.28. Вкладка диалогового окна Форматирование графика — Изменение вида графика

551

— в однострочном поле Color установите цвет — grn (зеленый);

— в однострочном поле Type установите: bar (прямоугольник);

— щелкните на кнопке OK. Новое представление графика изображено на рис. 7.29.

9. Чтобы добавить новый график к существующему:

— установите курсор на рабочем поле в строке справа от функции f(x);

— введите с клавиатуры: g(x):(1/x);

— нажмите клавишу <Enter>. На экране появится: g(x):=1 ;

x

—выделите график;

—щелкните на графике функции. Установите курсор справа от f(x);

—введите с клавиатуры запятую. Курсор перейдет на следующую строку;

552

—наберите на клавиатуре: g(x). Нажмите клавишу <Enter>;

—измените цену деления на оси Õ, изменив строку x:= –10..10 на x:= –10, –9.5..10;

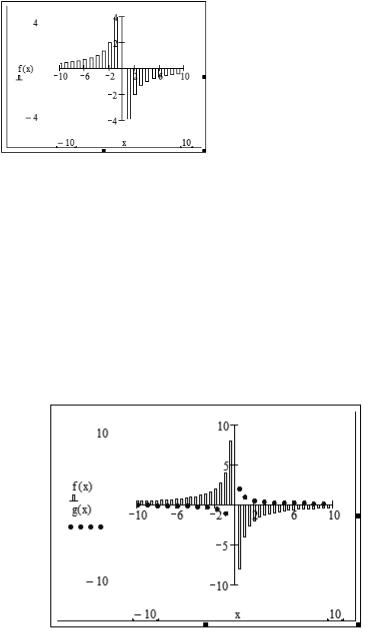
—линию графика g(x) изобразите по своему усмотрению, используя диалоговое окно Formatting Currently Selected X-Y Plot.

На рис. 7.30 выбран точечный график (Type — points, Weight — 3) голубого (blue) цвета.

Работа ¹ 2. Решение системы уравнений

Цель работы: изучить правила решения системы уравнений с помощью пакета MathCad.

Задание: решив систему уравнений

7x1 – x2 – 4x3 = 2,

–4x1 + x2 + 5x3 = 2, найти значения õ1, õ2, õ3.

Методика выполнения работы: вначале требуется обозна- чить переменные. Примем следующие обозначения:

A — матрица коэффициентов системы; B — вектор свободных членов;

X — вектор результатов решения.

1. Выведите на экран панели инструментов, необходимые для работы. Для этого:

— выполните команду F10 View Math Palette для вывода панели 1 (рис. 7.31);

>?@ABC ?MN EFG@DA HI@AJK>L-

>?@ABC DA EFG@DA HI@AJK>L-

Ðèñ 7.31. Панели инструментов пакета MathCAD, используемые при работе с матрицами

553

—щелкните на четвертой слева пиктограмме этой панели для вывода на экран панели 2 Matrix or Vector.

2. Задайте матрицу À коэффициентов системы:

—в левом верхнем углу рабочего поля окна документа щелкните левой кнопкой мыши;

—наберите прописными буквами: ORIGIN:=1, чтобы на- чать индексацию результатов решения системы с номера 1;

—щелкните в рабочей области окна в месте расположения матрицы;

—введите с клавиатуры имя матрицы: A;

—щелкните на пиктограмме с изображением стилизованной матрицы на панели 2;

—задайте размер матрицы À: 3 3;

—щелкните на кнопке ÎÊ;

• • •

— на экране появится заготовка для матрицы: A:= • • •

• • •

—введите значения элементов матрицы: установите курсор на верхнем левом черном прямоугольнике матрицы и введите значение: 7;

—нажмите клавишу <Tab>. Курсор переместится на одну ячейку вправо; последовательно введите значения:

7 1 4

6 6 1 4 1 5

Нажмите клавишу <Enter>.

3. Установите курсор в рабочей области окна под матрицей A и, последовательно выполняя указания пункта 2, введите

ñклавиатуры имя матрицы: Â:;

—нажмите комбинацию клавиш <Ctrl> + <M> и задайте размер матрицы Â: — 3 1;

2

— введите матрицу: Â: 1 ;

2

— нажмите клавишу <Enter>.

554

4. Создайте обратную матрицу A–1 :

—введите с клавиатуры: A. Нажмите комбинацию клавиш <Shift> + <6> и введите: –1. Введите с клавиатуры знак «=»;

—нажмите клавишу <Enter>.

5.Äëÿ нахождения корней системы линейных уравнений требуется вычислить определитель det. В изучаемом пакете вы- числение определителя осуществляется записью следующего выражения: det := | A |. Наберите его, используя соответствующую пиктограмму панели инструментов 2. Выведите на экран полученное значение: det=<Enter>. Появится запись: det=105. Если значение определителя det не равно нулю, т. е. матрица коэффициентов À невырождена, задача имеет однозначное решение во всех случаях, и для любого вектора Â найдется единственный вектор Õ, удовлетворяющий заданной системе уравнений (1).

6.Чтобы найти вектор Õ:

—введите с клавиатуры: X:A ^ –1:

—нажмите два раза клавишу <Æ> (вправо) и наберите: *B:

—нажмите клавишу <Enter>. На экране появится: X:=A–1·B. 7. Введите с клавиатуры: X= и нажмите клавишу <Enter>.

На экране появится результат решения: матрица 3 ¥ 1. Убедитесь, что все компоненты вектора Õ равны единице.

8. Чтобы вывести на экран значения Õ1, Õ2, Õ3:

—введите с клавиатуры: X[1= и нажмите клавишу <Enter>. На экране появится: X1= (значение первого корня);

—введите с клавиатуры: X[2= и нажмите клавишу <Enter>. На экране появится: X2= (значение второго корня);

—так же получите и значение третьего корня.

Работа ¹ 3. Решение нелинейных уравнений

Цель работы: поиск корня нелинейного уравнения с помощью функции Root пакета MathCad.

Задание: определить значение корня уравнения x + lg(x) + + ln(x/10) = 11.1 с точностью 10–3, если известно, что x [10;11].

Методика выполнения работы: многие уравнения не имеют

аналитических решений. Они могут решаться численными ме-

555

тодами с заданной погрешностью. Для простейших уравнений вида F(x) = 0 решение находится с помощью функции root (Выражение, Имя_переменной). Функция root возвращает значение переменной, при котором выражение становится равным нулю, т. е. F(x) = 0.

Для решения уравнения надо сначала задать начальное зна- чение переменной. Функция всегда имеет несколько решений, поэтому выбор решения определяется начальным значением переменной.

Введем условные обозначения:

f(x) — функция, приравниваемая к 0; TOL — точность вычисления;

x — начальное значение переменной;

x1 — приближенное решение функции f(x).

1. Выведите на экран панели инструментов, необходимые для работы:

—для вывода панели 1 ( см. рис. 7.31) выполните команду

<F10> View Math Palette;

—щелчком на первой пиктограмме панели 1 выведите на экран панель 4 Arithmetic Palette (Ñ÷åò), предназначенную для набора различных математических формул.

2. Задание вида функции и условий:

—в рабочей области экрана с клавиатуры введите функцию: f(x):= x + lg(x) + ln(x/10) — 11.1;

—в рабочей области экрана введите точность: TOL:=10–3 и начальное значение переменной: x:=10;

—функции, которые не заданы в MathCad в явном виде, необходимо выразить через другие функции, например: lg(x)= =ln(x)/ln(10).

3. Решение нелинейного уравнения с помощью функции root:

—в рабочей области экрана введите с клавиатуры: x1:=root(f(x),x);

—нажмите клавишу <Enter>.

4.Вывод на экран значения õ1:

—введите с клавиатуры: x1= <Enter>. На экране появится приближенное значение x1. По умолчанию количество знаков после запятой равно трем;

556

— если требуемая точность превышает 10–2, необходимо изменить формат вывода результата на экран, выполнив команду <F10> Format Number Displayed Precision.

7.2.3. Элементы численных методов

Численные методы — это методы приближенного или точ- ного решения задач математики, основанные на построении конечной последовательности действий над конечным множеством чисел. Численные методы являются предметом изуче- ния вычислительной математики. Для решения и исследования задач прикладной математики в настоящее время принята и представляется наиболее эффективной следующая методология.

1.Составляется математическая модель (ММ) процесса. Обычно ММ формулируется в терминах интегральных и дифференциальных уравнений функций непрерывного аргумента. Это так называемая континуальная ММ — экономный способ описания конечной совокупности (ансамбля) дискретных объектов, когда количество этих объектов становится большим (таковой ММ является, например, интегро-дифференциаль- ное уравнение Больцмана, описывающее поведение ансамбля частиц в некотором объеме).

2.Осуществляется переход от континуальной к дискретной

ÌÌ.Он заключается в замене функций непрерывного аргумента функциями дискретного аргумента, а уравнений континуальной ММ — конечно-разностными уравнениями. При этом интеграл заменяется конечной суммой, а производная — разностным отношением. В результате, как правило, приходят к системе большого количества уравнений с большим количе- ством неизвестных (дискретная ММ).

3.Составляется численный метод, или вычислительный алгоритм, для решения полученной системы уравнений с некоторой указанной точностью.

4.Производится программирование, т. е. перевод вычислительного алгоритма на язык ЭВМ.

Указанные этапы составляют «технологическую цепоч- ку» современной вычислительной математики. Содержащиеся

557

в ней переходы от исходной совокупности дискретных объектов (например, ансамбль молекул в заданном объеме газа) к континуальной модели, а затем к другой системе дискретных объектов (разностная сетка) необходимы для уменьшения объема перерабатываемой информации. Так, в нашем примере ансамбль очень большого количества частиц (1024) заменяется совокупностью ячеек сетки в значительно меньшем количестве (106).

Âэкономике конечная совокупность дискретных объектов, как правило, также непосредственно описывается дискретной моделью.

При переходе от континуальной к дискретной ММ производится замена континуального оператора соответствующим дискретным. Так, дифференциальный оператор заменяется разностным, интеграл — суммой и т. д. Такая замена приводит

êпоявлению погрешности аппроксимации. В практических вычислениях следует учитывать также погрешность округления, возникающую в ЭВМ при операциях над машинными числами, имеющими ограниченное количество значащих цифр. Учитывая это, получают реальный вычислительный алгоритм,

âотличие от теоретического вычислительного алгоритма. Это привело к необходимости проводить анализ погрешности округления и гарантированных оценок точности реальных вы- числений.

Существуют разнообразные численные методы для решения многих важных классов задач.

Основой численного метода решения задач математиче- ской физики является дискретизация задачи с последующим сведением полученных, вообще говоря, нелинейных уравнений к системе линейных алгебраических уравнений. В связи с этим численные методы по способу дискретизации можно подразделить на проекционные и конечно-разностные, а по способу решения линейной системы — на прямые и итерационные.

Âпоследнее время большое значение приобретают нерегулярные системы, к которым приводят задачи о потоках в различного рода сетях (тепловых и энергетических, в трубопроводах). Здесь теория разностных схем сочетается с теорией

графов.

558

7.2.4. Создание диалоговых программ

Проблема эффективного взаимодействия человека и ЭВМ возникла с появлением первых вычислительных машин. На на- чальном этапе внедрения ЭВМ непосредственно с ними работали только программисты и операторы, общение же специалистов в сфере управленческой деятельности происходило опосредованно: путем выдачи программистам заданий на разработку программ решения задач и последующего получения распечаток готовых результатов вычислений на ЭВМ.

Расширение сфер использования ЭВМ, совершенствование их аппаратных и программных средств, а главное — появление и широкое внедрение ПК привели к тому, что в процесс непосредственного взаимодействия с ЭВМ был вовлечен массовый пользователь.

Специфика работы пользователей ПК требует создания таких средств и методов общения с вычислительной системой, благодаря которым они (пользователи), не зная архитектуры и принципов функционирования ЭВМ, не владея профессиональными приемами программирования, могли бы удовлетворять свои информационные потребности в ходе взаимодействия с машиной.

Человек и компьютер в процессе решения различных задач, связанных с обработкой информации, могут взаимодействовать в различных режимах. Различают пакетный è интерактивный (запросный, диалоговый) режимы взаимодействия пользователя с ЭВМ. Сами же ЭВМ также могут работать в различных режимах: одно- и многопрограммном, разделения времени, реального времени, телеобработки и т. д. При этом разработчики имеют целью удовлетворение потребности пользователей в максимально возможной автоматизации решения разнообразных задач.

Пакетный режим был наиболее распространен в практике централизованного решения задач, когда большой удельный вес занимали задачи отчетности о производственно-хозяйст- венной деятельности экономических объектов разного уровня управления.

Организация вычислительного процесса при пакетном режиме строилась без доступа пользователя к ЭВМ. Его функции

559

ограничивались подготовкой исходных данных по комплексу организационно взаимосвязанных задач и передачей их в центр обработки, где формировался пакет, включающий задание ЭВМ на обработку программы, исходные, нормативно-расце- ночные и справочные данные. Пакет вводился в ЭВМ и реализовывался в автоматическом режиме без участия пользователя и оператора, что позволяло минимизировать время выполнения заданного набора задач. При этом работа ЭВМ могла проходить в однопрограммном или многопрограммном — что предпочтительнее — режиме, так как обеспечивалась параллельная работа основных устройств машины. В настоящее время пакетный режим реализуется применительно к электронной печати.

Интерактивный режим предусматривает непосредственное взаимодействие пользователя с информационно-вычислитель- ной системой и может носить характер запроса (как правило, регламентированного) или диалога с ЭВМ.

Запросный режим необходим пользователям для взаимодействия с системой через значительное число абонентских терминальных устройств (в том числе удаленных на довольно большое расстояние от центра обработки) с целью решения оперативных задач справочно-информационного характера (например, резервирование билетов на транспорте, номеров в гостиничных комплексах и т. п.). ЭВМ в подобных случаях реализует систему массового обслуживания, работает в режиме разделения времени, при котором несколько независимых абонентов (пользователей) с помощью устройств ввода-вывода имеют в процессе решения своих задач непосредственный и практически одновременный доступ к ЭВМ. Запросный режим позволяет дифференцированно, в строго установленном порядке предоставлять каждому пользователю время для общения с ЭВМ, а после окончания сеанса отключать его.

Диалоговый режим открывает пользователю возможность непосредственно взаимодействовать с вычислительной системой в допустимом для него темпе работы, реализуя повторяющийся цикл выдачи задания, получения и анализа ответа. При этом ЭВМ сама может инициировать диалог, сообщая пользователю последовательность шагов (представление меню) для получения искомого результата.

560