3. Угловая модуляция

Фазовая и частотная модуляция тесно связаны друг с другом. Поэтому они часто называются одним термином – угловая модуляция (УМ). Рассмотрим сходства и различия этих двух видов модуляции.

3.1. Фазовая модуляция

Пусть модулирующий сигнал линейно действует на фазу несущего колебания:

.

Тогда мы получаем сигнал с фазовой модуляцией(ФМ):

.

Весь аргумент называется полной фазойколебания:

.

Введем понятие мгновенной частоты, равной производной от полной фазы по времени:

Видно, что в случае фазовой модуляции изменяется не только фаза, но и мгновенная частота колебания.

Полная фаза может быть найдена путем интегрирования мгновенной частоты:

3.2. Частотная модуляция

Пусть модулирующий сигнал линейно связан с мгновенной частотой колебания:

Добавка в виде константы необходима для того, чтобы сделать колебание высокочастотным.

Полная фаза находится путем интегрирования мгновенной частоты:

Здесь – произвольная постоянная.

Частотно-модулированныйсигнал (ЧМ) имеет следующий вид:

Как видно, начальная фаза колебания при частотной модуляции претерпевает изменения, пропорциональные интегралу от модулирующего сигнала:

Таким образом, фазовая и частотная модуляция оказываются тесно связанными.

Рис. 12. Взаимосвязь фазовой и частотной модуляции

С помощью фазового модулятора можно получить частотно-модулированное колебание. Для этого необходимо проинтегрировать модулирующий сигнал до подачи на модулятор. Интегрирование низкочастотного модулирующего сигнала можно рассматривать как внешнюю (стороннюю) функцию по отношению к модулятору.

Аналогично, используя частотный модулятор, можно получить фазово-модулированное колебание. Для этого нужно пропустить модулирующий сигнал через дифференцирующее устройство до подачи на модулятор.

3.3. Гармоническая угловая модуляция

Рассмотрим случай гармонического модулирующего сигнала. Начальная фаза колебаний изменяется при этом по гармоническому закону:

Коэффициент называетсяиндексом угловой модуляции. Он определяет интенсивность изменения начальной фазы.

Полная фаза колебания:

Сам сигнал с гармонической модуляцией:

Как уже говорилось, при изменении начальной фазы изменяется и мгновенная частота:

В данном случае мгновенная частота изменяется также по гармоническому закону. Как видно из формулы, ее максимальное отклонение от среднего значения составляет. Эта величина называетсядевиацией частотыи обозначается. Таким образом, индекс угловой модуляции можно выразить через девиацию частоты:

Итак, при гармонической угловой модуляции и начальная фаза, и мгновенная частота меняются по гармоническому закону. Различия между фазовой и частотной модуляцией становятся заметными лишь при изменении модулирующей частоты .

При фазовой модуляции индекс от частоты модулирующего сигнала не зависит, а девиация частоты прямо пропорциональна:

При частотной модуляции, параметром, не зависящим от модулирующего сигнала, является девиация частоты . Индекс модуляцииоказывается обратно пропорциональным:

Рис. 13. Зависимость индекса модуляции (слева) и девиации частоты (справа) от частоты модулирующего сигнала в случае ФМ и ЧМ

В общем случае спектр сигнала с гармонической угловой модуляцией выражается через функции Бесселя 1-го рода.

В частном случае малого индекса модуляции () можно получить простое приближенное решение:

Для можно приближенно считать, что:

Тогда:

Полученный результат напоминает представление АМ сигнала с гармонической модуляцией – тоже три составляющих с теми же частотами, амплитуды рассчитываются аналогично. Единственное отличие в знаке минус перед одной из боковых частот.

Рис. 14. Амплитудный (сверху) и фазовый (снизу) спектры сигнала с гармонической УМ при

Спектральные представления АМ и УМ сигналов различаются только знаком перед одним из слагаемых. Из векторной диаграммы видно, как сложение боковых частот, приводит к качанию результирующего вектора относительно несущего колебания.

Методов, которые используются для демодуляции УМ довольно много. Все зависит от конкретного применения.

Рис. 15. Векторная диаграмма сигнала с гармонической УМ

Необходимо отметить, что различные фазовые и частотные детекторы применяются не только для детектирования специально модулированных сигналов, как например, в УКВ вещании и телевидении, но и для диагностики и стабилизации параметров различных технических систем.

В качестве иллюстрации современного подхода построения УМ демодулятора рассмотрим схему квадратурной обработки, которая пригодна для реализации в реальном масштабе времени как с использованием аналоговой обработки сигналов, так и с использованием цифровой обработки сигналов.

При квадратурной обработке входной сигнал умножается на два опорных колебания, сдвиг по фазе между которыми составляет 90 º:

Результат каждого из умножений содержит два слагаемых. Одно из них – низкочастотное (косинус или синус начальной фазы), другое – высо­ко­частотное (УМ-сигнал с удвоенной частотой). Низкочастотные составляющие выделяются с помощью ФНЧ:

Дальнейшие действия зависят от вида угловой модуляции.

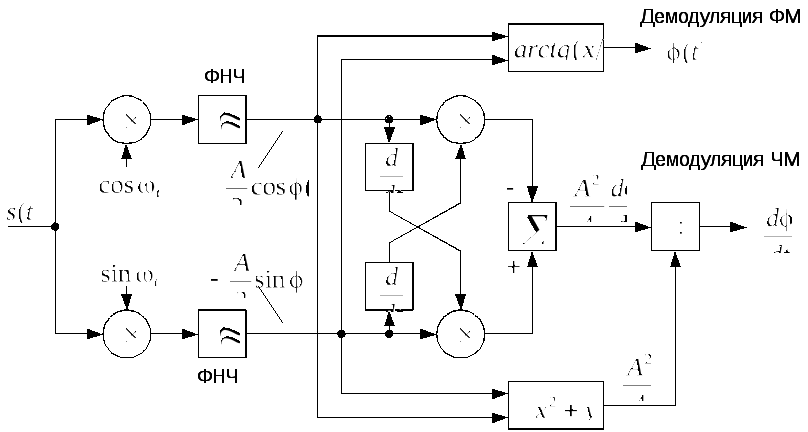
Рис. 16. Структурная схема демодулятора УМ с выходами фазового и частотного канала

Для демодуляции ФМ необходимо вычислить фазу из полученной пары квадратурных составляющих:

При обработке низкочастотных сигналов цифровым способом никаких проблем с вычислением фазы не возникает.

При необходимости фазу можно вычислить и в аналоговом виде. Для небольших индексов угловой модуляции () функцию арктангенса можно аппроксимировать с помощью операционных усилителей, охваченных нелинейной обратной связью. Функция деления осуществляется в специализированных аналоговых умножителях.

Для демодуляции ЧМ полученную фазовую функцию необходимо продифференцировать: