§ 9.2 Параметрические критерии

t-критерий Стьюдента (t-распределение). Использование формулы Гаусса-Лапласа (44) для сравнительной оценки средних величин затруднено тем, что в качестве аргументов в эту формулу входят генеральные параметры μ и σ (которые, как правило, остаются неизвестными), тогда как при обработке и сравнении выборочных групп приходится пользоваться не генеральными, а выборочными характеристиками и. Учитывая это обстоятельство, английский математик В.Госсет (Стьюдент), в 1908 г. нашел закон распределения величины, в которой генеральный параметрσ заменен на его выборочную характеристику 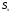, т.е. нашелзакон распределения значений

. (1)

Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:

для , (2)

где С – константа, зависящая от числа степеней свободы .

Открытый Стьюдентом и теоретически обоснованный Р. Фишером закон t-распределения служит основой так называемой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки.

t-распределение зависит только от числа степеней свободы , причем с увеличением объема выборкиn t-распределение быстро приближается к нормальному с параметрами μ = 0 и σ = 1 и уже при не отличается от него.

Более наглядное представление о характере t-распределения дает рис. 20, на котором на фоне нормальной кривой изображена (более пологая) кривая t-распределения при n = 3. t-распределение симметрично и отражает специфику распределения средней арифметической в случае малой выборки в зависимости от ее объема n. Для выборок, объем которых превышает 30 единиц, величина t распределяется нормально и не зависит от числа наблюдений. Если же , то характерt-распределения находится в зависимости от числа наблюдений n.

Рис. 9.1 Кривая t-распределения (1) при n = 3 на фоне

нормальной кривой (2)

Для практического использования t-распределения составлена специальная таблица, в которой содержатся критические точки t_st для разных уровней значимости α и чисел степеней свободы k.

Оценка разности средних. Сравнивая друг с другом две независимые выборки, взятые из нормально распределяющихся совокупностей с параметрами μ₁ и μ₂, можно предположить, что , а дисперсия этой разностиσ²_D. Значения генеральных параметров неизвестны, однако несложно найти величины выборочных средних и разность между ними 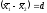. Нулевая гипотеза сводится к предположению, что. Критерием для проверкиН₀-гипотезы служит отношение

, (3)

где t – переменная величина, следующая t-распределению Стьюдента с числом степеней свободы , а– ошибка указанной разности, обозначаемая в дальнейшем символомS_d.

Так как, согласно Н₀-гипотезе, , тоt-критерий выражается в виде отношения разности выборочных средних к своей ошибке, т.е.

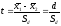. (4)

H₀-гипотезу отвергают, если фактически установленная величина t-критерия t_ф превзойдет или окажется равной критическому (стандартному) значению t_st этой величины для принятого уровня значимости α и числа степеней свободы , т.е. при условии.

Ошибку разности средних S_d определяют по следующим формулам:

а) для равночисленных выборок, т.е. при ,

; (5)

б) для неравночисленных выборок, т.е. при

. (6)

Неопровержение Н₀-гипотезы нельзя рассматривать как доказательство равенства между неизвестными параметрами совокупностей, из которых извлечены сравниваемые выборки. В таких случаях вопрос о преимуществе одной статистической совокупности перед другой остается открытым. Ведь не исключено, что при повторных испытаниях Н₀-гипотеза может оказаться несостоятельной. Более того, и в тех случаях, когда Н₀-гипотеза опровергается, не следует спешить с окончательным выводом.

Следует заметить, что вышеизложенное применение t-критерия предполагает, что дисперсии сравниваемых групп одинаковы: . Если это не так, то величину критерия находят по формуле

, (7)

а число степеней свободы – по следующим формулам:

а) при .

б) при

Правильное применение t-критерия предполагает нормальное распределение совокупностей, из которых извлечены сравниваемые выборки, и равенство генеральных дисперсий. Если эти условия не выполняются, то t-критерий применять не следует. В таких случаях более эффективными будут непараметрические критерии.

Оценки средней разности между выборками с попарно связанными вариантами. Сравниваемые выборки нередко представляют собой ряды попарно связанных вариант, т.е. являются зависимыми выборками. В таких случаях оценкой разности между генеральными средними будетсредняя разность, определяемая из суммы разностей между попарно связанными вариантами сравниваемых групп, т.е.

. (8)

Оценкой генеральной дисперсии σ² разности средних будет выборочная дисперсия

. (9)

В формулах (8) и (9) n – число парных наблюдений; .

Ошибку средней разности , обозначаемую символомS_d, определяют по формулам

(10)

или

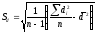. (11)

Если члены генеральной совокупности распределяются нормально, то и разности между ними будут распределяться нормально и случайная величина будет иметь распределение Стьюдента с степенями свободы. Н₀-гипотеза сводится в виде отношения средней разности к своей ошибке, т.е. . Еслидля принятого уровня значимости и числа степеней свободы, то нулевая гипотеза должна быть отвергнута.

Оценку средней разности можно произвести по доверительному интервалу, построенному на основании полученной разности и ее ошибки. Если нижняя граница доверительного интервала окажется с положительным знаком, то это будет свидетельствовать о достоверности разницы. Если же нижняя граница доверительного интервала будет с отрицательным знаком, то это служить указанием на случайный характер наблюдаемой средней разности.

Оценка разности между долями. Выборочная доля зависит от числа единиц в выборке, имеющих учитываемый признак, а общее число таких единиц в генеральной совокупности определяет генеральную долю 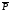. Оценкой разности между генеральными долямислужит разность между выборочными долями. Отношение этой разности к своей ошибке дает случайную величину, которая следуетt-распределению Стьюдента. Н₀-гипотезу, или предположение о том, что , отвергают, еслидляи принятого уровня значимостиα. Ошибка разности между долями, взятыми из приблизительно равновеликих выборок (когда численность групп различаются не более чем на 25%), вычисляют по формуле

, (12)

где . Если доли выражены в процентах от общего числа наблюдений, ошибку разности между ними определяют по формуле

. (13)

Сопоставимые группы n₁ и n₂ могут быть выражены абсолютными числами m₁ и m₂. Ошибка наблюдаемой между ними разности определяется по следующей формуле:

, (14)

но так как ;;;, то формулу (12) можно представить и в таком виде:

. (15)

Когда сравнивают доли из неравновеликих выборок и при , ошибку разности между ними определяют по формуле

; (16)

p определяют как средневзвешенную из p₁ и p₂ долей, или же из абсолютных численностей групп:

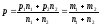. (17)

В этих формулах n₁ и n₂ – численности групп, на которых определяют доли и. Если доли выражают в процентах отn, то вместо нужно брать. Если же неравновеликие группы выражены абсолютными числамиm₁ и m₂, ошибку разности между ними определяют по формуле

. (18)

Описанные выше критерии проверки равенства долей в двух выборках оказывается пригодными при не слишком больших и не слишком малых значениях p (). Особенно это относится к случаю небольших выборок. Свободным от подобного рода ограничений и поэтому более универсальным оказывается способ проверки равенства долей, основанный на использованииугловой трансформации (φ-преобразования Фишера). При этом методе сравниваемые доли выражают в процентах с введением поправки Йейтса на непрерывность, равной , которую вычитают из большей и прибавляют к меньшей доле. Затем по таблице значенийнаходят величины дляисправленных долей: и, берут их разность и относят ее к ошибке, определяемой по формуле

. (19)

Условием для непринятия нулевой гипотезы служит следующее выражение:

(20)

для числа степеней свободы и принятого уровня значимостиα.

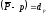Оценка разности между выборочной и генеральной долями. При оценке разности между известной генеральной долей и долей выборкиp нулевая гипотеза сводиться к предположению, что разница между ними возникла случайно. Критерий Стьюдента в таких случаях выражается в виде отношения разности к своей ошибке, которую определяют по формуле

, (21)

где n – объем выборки. Условием для непринятия нулевой гипотезы служит критерий дляи принятого уровня значимостиα.

F-критерий Фишера (F-распределение). Для проверки Н₀-гипотезы о равенстве генеральных дисперсий () нормально распределяющихся генеральных совокупностейt-критерий оказывается недостаточно точным, особенно при оценке разности дисперсий малочисленных выборок. В поисках лучшего критерия Р. Фишер нашел, что вместо выборочной разности удобнее использовать разность между натуральными логарифмами этих величин, т.е., где. Эта разность, обозначаемая буквойz, распределяется нормально при наличии как больших, так и средних по объему статистических совокупностей.

Д. Снедекор предложил вместо логарифма отношений использовать отношения выборочных дисперсий, обозначив этот показатель в честь Фишера буквой F, т.е.

при . (22)

Так как принято брать отношение большей дисперсии к меньшей, то критерий . Если, то. Чем значительнее неравенство между выборочными дисперсиями, тем больше будет и величинаF, и, наоборот, чем меньше окажется разница между дисперсиями, тем меньше будет величина F.

Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы 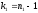и.F полностью определяется выборочными дисперсиями и не зависит от генеральных параметров, так как предполагают, что сравниваемые выборки, характеризуемые дисперсиями и, взяты из генеральных совокупностей сили с одной и той же генеральной совокупности. Функция распределения возможных значений величиныF при небольшом n имеет форму асимметричной кривой, которая по мере увеличения числа испытаний () приближается к кривой нормального распределения.

Функция F-распределения табулирована для 5%-ного и 1%-ного уровней значимости и чисел степеней свободы k₁ для большей дисперсии и k₂ для меньшей. Если выборки взяты из разных совокупностей с их параметрами и, не равными друг другу, тои нулевая гипотеза должна быть отвергнута.

F-критерий можно применить и для оценки разности между долями из неравновеликих выборок. Нулевая гипотеза отвергается при условии, что

для и.

Если оценивают разность между средними ивыборок, извлечены из совокупностей, которые распределяются по закону Пуассона,F-критерий строят в виде отношения

для и, а также принятого уровня значимостиα.

Оценка разности между коэффициентами вариации. Разность между коэффициентами вариации сравниваемых групп, извлеченных из нормально распределяющихся совокупностей, можно оценить с помощью t-критерия Стьюдента. Приближенной оценкой разности служит ее отношение к своей ошибке, определяемая по формуле

. (23)

Нулевую гипотезу отвергают, если для принятого уровня значимости и числа степеней свободы.

Разность между коэффициентами вариации можно оценить путем сопоставления доверительных интервалов, построенных для генеральных параметров сравниваемых групп. При этом границы доверительных интервалов определяют по формулам

;

где P_н – нижняя, а Р_в – верхняя границы доверительного интервала; ;t – нормированное отклонение (для ).