
Конспект лекции 1
.docxЛекция 1. Векторы на плоскости и в пространстве, сложение и вычитание векторов, их свойства.
Литература. [1] § 1 ‑ 4.
Отрезок
называется направленным, если для
него указан порядок его концов. Первый
из них называется началом, а второй
концом направленного отрезка. На
рисунках конец такого отрезка обозначается
стрелкой (рис. 1). Если M начало, а N
конец направленного отрезка, то будем
его обозначать как
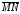 .
.
Определение 1. Направленные отрезки, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Если коллинеарные направленные отрезки имеют одинаковые направления, то они называются сонаправленными, если их направления различны, то - противоположно направленными
Коллинеарные
направленные отрезки будем обозначать
как
 .
Сонаправленные и противоположно
направленные отрезки обозначаются
соответственно через
.
Сонаправленные и противоположно
направленные отрезки обозначаются
соответственно через
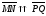 и
и
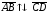 .
.
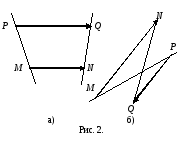
Пусть
 и
и
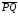 коллинеарные направленные отрезки, не
лежащие на одной прямой. Отрезки
сонаправлены в том и только в том случае,
когда их концы N и Q лежат в одной
полуплоскости относительно прямой MP,
проходящей через их начала (рис. 2 а).
Отсюда следует, что
коллинеарные направленные отрезки, не
лежащие на одной прямой. Отрезки
сонаправлены в том и только в том случае,
когда их концы N и Q лежат в одной
полуплоскости относительно прямой MP,
проходящей через их начала (рис. 2 а).
Отсюда следует, что
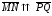 тогда и только тогда, когда отрезки MP
и NQ не пересекаются. Если
тогда и только тогда, когда отрезки MP
и NQ не пересекаются. Если
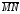 и
и
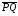 противоположно направлены и не лежат
на одной прямой, то их концы N и Q
принадлежат различным полуплоскостям
относительно прямой MP. Таким образом,
противоположно направлены и не лежат
на одной прямой, то их концы N и Q
принадлежат различным полуплоскостям
относительно прямой MP. Таким образом,
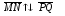 в
том и только в том случае, когда отрезки
MP и NQ пересекаются (рис. 2 б).
в
том и только в том случае, когда отрезки
MP и NQ пересекаются (рис. 2 б).
Под
длиной направленного отрезка
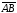 понимается расстояние между точками А
и В. Направленный отрезок называется
нулевым, если его начало совпадает
с его концом. У такого отрезка длина
равна нулю, считается, что его направление
произвольное, т.е. он сонаправлен с
любым отрезком. Будем его обозначать
как
понимается расстояние между точками А
и В. Направленный отрезок называется
нулевым, если его начало совпадает
с его концом. У такого отрезка длина
равна нулю, считается, что его направление
произвольное, т.е. он сонаправлен с
любым отрезком. Будем его обозначать
как
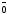
Бинарное отношение называется отношением эквивалентности, если выполнены следующие три условия:
- рефлексивности - любой элемент множества находится в бинарном отношении сам с собой (a a );
- симметричности - если элемент a находится в бинарном отношении с элементом b, то b также находится в бинарном отношении с элементом a (если a b, то b a);
- транзитивности - если элемент a находится в бинарном отношении с элементом b, а b, в свою очередь, с элементом с, то а находится в том же отношении с с (если a b и b c, то a c).
Пример 1. На множестве направленных отрезков введено бинарное отношение : два отрезка находятся этом отношении, если они коллинеарны. Будет ли отношением эквивалентности?
Решение.
Не выполняется ли условие
транзитивности. Нам следует проверить,
что из
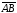
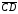 и
и
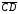
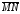 вытекает:
вытекает:
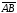
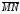 .
Пусть
.
Пусть
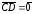 .
Нулевой вектор сонаправлен любому
вектору, поэтому из условий
.
Нулевой вектор сонаправлен любому
вектору, поэтому из условий
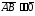 и
и
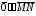 не
следует, что
не
следует, что
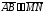 .
Данное бинарное отношение не является
отношением эквивалентности.
.
Данное бинарное отношение не является
отношением эквивалентности.
Если на множестве введено отношение эквивалентности, то оно естественным образом разбивается на непересекающиеся подмножестве - классы эквивалентностей. Их образуют все те элементы множества, которые эквивалентны между собой. Введем понятие равенства двух направленных отрезков,
Определение 2. Два ненулевых направленных отрезка называются равными друг другу, если они сонаправлены и их длины одинаковы. Два нулевых направленных отрезка всегда равны между собой.
Свойство 1. Отношение равенства направленных отрезков является отношением эквивалентности.
Действительно,
любой направленный отрезок равен самому
себе. Если
 ,
то
,
то
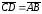 .
Если
.
Если
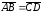 и
и
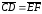 ,
то длины этих трех отрезков одинаковы,
а их направления совпадают, Поэтому
,
то длины этих трех отрезков одинаковы,
а их направления совпадают, Поэтому
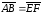 . Свойство
2. Отрезок
. Свойство
2. Отрезок
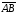 равен отрезку
равен отрезку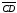 в том и только в том случае, когда середины
отрезков AD и BC совпадают.
в том и только в том случае, когда середины
отрезков AD и BC совпадают.
Если
равные отрезки
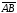 и
и
 не лежат на одной прямой (рис 3 а), то
четырехугольник ABCD - параллелограмм,
его диагонали в точке пересечения
делятся пополам. Наоборот, если отрезки
AD и BC в точек пересечения делятся
пополам, то четырехугольник ABCD -
параллелограмм, поэтому
не лежат на одной прямой (рис 3 а), то
четырехугольник ABCD - параллелограмм,
его диагонали в точке пересечения
делятся пополам. Наоборот, если отрезки
AD и BC в точек пересечения делятся
пополам, то четырехугольник ABCD -
параллелограмм, поэтому
 и
и
 .
.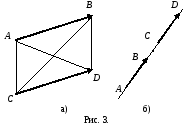
Свойство 2 справедливо также и для отрезков, лежащих на одной прямой (рис. 3 б). Проверьте самостоятельно.
Свойство
3. Отрезок
 равен отрезку
равен отрезку
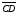 тогда и только тогда, когда
тогда и только тогда, когда
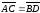 .
.
Доказательство этого свойства аналогично предыдущему.
Cвойство
4. Если даны направленный отрезок
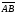 и точка С, то существует единственная
точка D, для которой
и точка С, то существует единственная
точка D, для которой
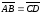 .
.
Действительно,
через точку С всегда можно провести
прямую, параллельную AB, а затем
выбрать на ней такую точку D, для
которой отрезки
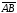 и
и
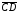 равны друг другу.
равны друг другу.
Определение 3. Вектором называется класс равных между собой направленных отрезков.
Для
обозначения векторов будем использовать
строчные латинские буквы со стрелкой
сверху:
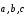 .
Направленный отрезок, принадлежащий
вектору, будем называть его представителем.
Если дан направленный отрезок
.
Направленный отрезок, принадлежащий
вектору, будем называть его представителем.
Если дан направленный отрезок
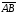 и мы рассматриваем вектор, которому
принадлежит этот отрезок, то будем
обозначать его через
и мы рассматриваем вектор, которому
принадлежит этот отрезок, то будем
обозначать его через
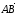 .
От любой точки плоскости можно
“отложить данный вектор”, т.е. построить
его представитель с началом в этой
точке.
.
От любой точки плоскости можно
“отложить данный вектор”, т.е. построить
его представитель с началом в этой
точке.
Легко
видеть, что все нулевые направленные
отрезки равны между собой. Действительно,
у каждого из них длина равна 0 и они
сонаправлены друг с другом. Вектор,
представителем которого является
нулевой направленный отрезок, называется
нулевым. Он будет нами обозначаться
через
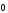 .
.
Как следует из определения 2, все равные
между собой направленные отрезки имеют
одну и ту же длину, Её мы будем называть
длиной или модулем вектора, и
обозначать через
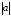 или
или
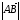 .
Модуль нулевого вектора равен нулю.
Если два вектора имеют одинаковый
модуль, но противоположные направления,
то их будем называть противоположными.
Вектор, противоположный
.
Модуль нулевого вектора равен нулю.
Если два вектора имеют одинаковый
модуль, но противоположные направления,
то их будем называть противоположными.
Вектор, противоположный
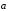 ,
будет обозначаться как
,
будет обозначаться как
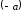 .
.
Векторы
назовем соответственно коллинеарными,
сонаправленными или противоположно
направленными, если коллинеарны,
сонаправлены или противоположно
направлены любые два его представителя.
Очевидно, что это определение не зависит
от выбора представителей векторов.
Обозначать коллинеарные, сонаправленные
и противоположно направленные векторы
будем соответственно через:
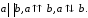 Систему векторов
Систему векторов
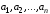 будем называть коллинеарной, если любые
два вектора системы коллинеарны друг
другу.
будем называть коллинеарной, если любые
два вектора системы коллинеарны друг
другу.
Будем говорить, что вектор параллелен прямой, если его представитель параллелен или лежит на этой прямой. Очевидно, что введенное понятие не зависит от выбора представителя вектора. Ясно, что система векторов коллинеарна в том и только в том случае, когда существует прямая линия, которой параллельны все векторы системы.
Сложение и вычитание векторов
Определение 1. Пусть даны векторы
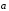 и
и
 .От
точки А отложим вектор
.От
точки А отложим вектор
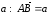 ,
а от конца направленного отрезка
,
а от конца направленного отрезка
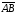 отложим вектор
отложим вектор
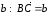 .
Вектор
.
Вектор
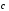 ,
определенный направленным отрезком
,
определенный направленным отрезком
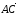 ,
называется суммой векторов
,
называется суммой векторов
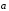 и
и
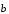 :
:
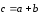 .
.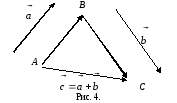
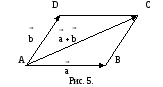
Построение суммы векторов
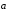 и
и
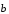 показано на рисунке 4. Из определения 1
следует, что для любых трех точек А,
В и С выполнено равенство:
показано на рисунке 4. Из определения 1
следует, что для любых трех точек А,
В и С выполнено равенство:
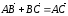 ,
Поэтому такой способ сложения векторов
часто называют правилом треугольника.
Наряду с ним используется еще один
способ определения суммы векторов -
правило параллелограмма. Если
,
Поэтому такой способ сложения векторов
часто называют правилом треугольника.
Наряду с ним используется еще один
способ определения суммы векторов -
правило параллелограмма. Если
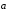 и
и
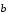 - два неколлинеарных вектора, то для
построения суммы
- два неколлинеарных вектора, то для
построения суммы
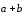 по правилу параллелограмма отложим их
от одной точки:
по правилу параллелограмма отложим их
от одной точки:
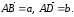 Затем треугольник ABD достроим до
параллелограмма ABCD. Искомая сумма
равна вектору
Затем треугольник ABD достроим до
параллелограмма ABCD. Искомая сумма
равна вектору
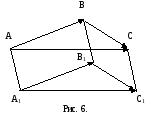
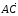 (рис. 5). Для обоснования корректности
определения 1 следует проверить, что
сумма векторов
(рис. 5). Для обоснования корректности
определения 1 следует проверить, что
сумма векторов
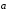 и
и
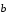 не зависит от выбора начальной точки
А. Действительно, возьмем две точки
А и А
не зависит от выбора начальной точки
А. Действительно, возьмем две точки
А и А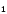 ,
отложим от них же вектор
,
отложим от них же вектор
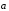 :
:
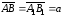 ,
от точек B и B
,
от точек B и B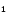 отложим вектор
отложим вектор
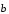 :
:
 (рис. 6). Так как
(рис. 6). Так как
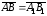 ,
то
,
то
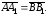 Аналогично, из равенства
Аналогично, из равенства
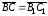 вытекает
вытекает
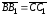 .
Следовательно,
.
Следовательно,
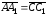 ,
откуда получим, что
,
откуда получим, что
 .
.
Рассмотрим свойства операции сложения векторов.
Свойство 1. Для любых векторов
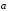 и
и
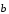 справедливо равенство:
справедливо равенство: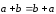 .
(свойство коммутативности).
.
(свойство коммутативности).
Доказательство. Отложим от точки
А вектор
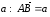 ,
а от точки В вектор
,
а от точки В вектор
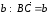 .
Тогда
.
Тогда
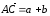 (рис. 7). Теперь отложим от точки А
вектор
(рис. 7). Теперь отложим от точки А
вектор
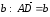 ,
Так как направленные отрезки
,
Так как направленные отрезки
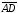 и
и
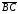 равны друг другу, то
равны друг другу, то
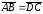 (см. свойство 3, §
1). Отсюда следует, что
(см. свойство 3, §
1). Отсюда следует, что
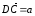 ,
т.е.
,
т.е.
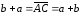 .
Свойство доказано.
.
Свойство доказано.
Свойство 2. Для любых векторов
 и
и
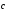 выполнено равенство:
выполнено равенство:
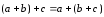 (свойство ассоциативности).
(свойство ассоциативности).
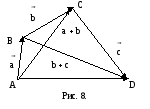
Доказательство. Отложим
последовательно от точки А вектор
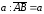 ,
от точки В вектор
,
от точки В вектор
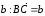 ,
а от точки С вектор
,
а от точки С вектор
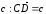 (рис. 8). Тогда
(рис. 8). Тогда
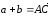 и из равенств
и из равенств
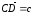 ,
,
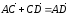 следует,
следует,
 С другой стороны,
С другой стороны,
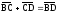 ,
поэтому
,
поэтому
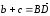 .
Так как
.
Так как
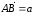 и
и
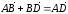 ,
то
,
то
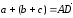 .
Свойство доказано.
.
Свойство доказано.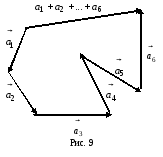
Свойство 2 позволяет определить сумму
любого числа векторов
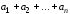 .
Она равна результату последовательного
суммирования
.
Она равна результату последовательного
суммирования
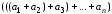 ,
к сумме первых двух векторов прибавляется
третий, затем четвертый и т.д. Из свойства
1 вытекает, что результат суммирования
любого числа векторов не зависит от
порядка суммирования. На рисунке 9
изображен процесс построения суммы
шести векторов.
,
к сумме первых двух векторов прибавляется
третий, затем четвертый и т.д. Из свойства
1 вытекает, что результат суммирования
любого числа векторов не зависит от
порядка суммирования. На рисунке 9
изображен процесс построения суммы
шести векторов.
Свойство 3. Для любого вектора
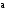 выполнено соотношение:
выполнено соотношение:
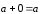 .
.
Доказательство. Отложим от точки
А вектор
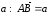 ,
а от точки В вектор
,
а от точки В вектор
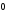 .
Так как
.
Так как
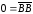 ,
то
,
то
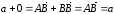 .
Свойство доказано.
.
Свойство доказано.
Свойство 4. Для любого вектора
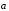 его сумма с противоположным вектором
его сумма с противоположным вектором
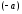 равна нулевому вектору:
равна нулевому вектору:
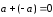 .
.
Доказательство. Вектор
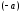 ,
противоположный
,
противоположный
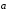 ,
имеет ту же длину, что и
,
имеет ту же длину, что и
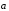 ,
но противоположное направление. Отложим
от точки А вектор
,
но противоположное направление. Отложим
от точки А вектор
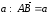 .
Если от точки В отложить вектор
.
Если от точки В отложить вектор
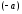 ,
то его конец совпадет с точкой А.
Поэтому
,
то его конец совпадет с точкой А.
Поэтому
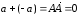 .
Свойство доказано.
.
Свойство доказано.
При суммировании векторов, вообще
говоря, их модули не складываются.
Действительно, возьмем два произвольных
вектора
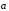 и
и
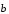 .
Отложим от точки А вектор
.
Отложим от точки А вектор
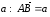 ,
а от точки В вектор
,
а от точки В вектор
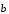 ,
получим:
,
получим: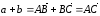 .
Пусть векторы
.
Пусть векторы
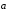 и
и
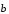 не коллинеарные. Тогда точки А, В
и С лежат в вершинах треугольника.
Исходя из неравенства треугольника
получим
не коллинеарные. Тогда точки А, В
и С лежат в вершинах треугольника.
Исходя из неравенства треугольника
получим
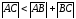 ,
т.е.
,
т.е.
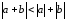 .
Пусть теперь векторы
.
Пусть теперь векторы
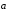 и
и
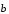 коллинеарные. Если они сонаправлены,
то точка В лежит между А и С,
поэтому
коллинеарные. Если они сонаправлены,
то точка В лежит между А и С,
поэтому
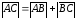 ,
т.е.
,
т.е.
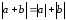 .
Если они противоположно направлены, то
точка В не лежит между А и С,
тогда
.
Если они противоположно направлены, то
точка В не лежит между А и С,
тогда
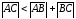 ,
т.е.
,
т.е.
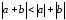 .
Таким образом, нами доказано неравенство:
.
Таким образом, нами доказано неравенство:
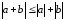 .
.
Определение 2. Под разностью двух
векторов
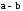 понимается вектор
понимается вектор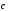 ,
удовлетворяющий условию:
,
удовлетворяющий условию:
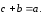
Пусть даны два вектора
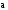 и
и
 .
Рассмотрим сумму вектора
.
Рассмотрим сумму вектора
 и вектор, противоположного
и вектор, противоположного
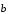 :
:
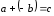 .
Докажем, что
.
Докажем, что
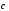
 удовлетворяет
условию:
удовлетворяет
условию:
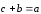 .
Используем свойства 3 и 4 операции
сложения:
.
Используем свойства 3 и 4 операции
сложения:
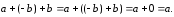
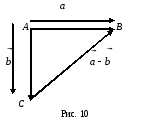
Можно найти разность
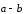 иначе. Для этого отложим векторы
иначе. Для этого отложим векторы
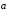 и
и
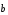 от одной точки A:
от одной точки A:
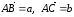 (рис. 10). Соединив концы C и B,
выберем направление отрезка СВ от
вычитаемого к уменьшаемому, т.е. от
вектора
(рис. 10). Соединив концы C и B,
выберем направление отрезка СВ от
вычитаемого к уменьшаемому, т.е. от
вектора
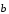 к вектору
к вектору
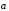 ,
от С к В. Так как
,
от С к В. Так как
 ,
то
,
то
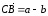 .
.
Для модуля разности двух векторов
справедливы неравенства
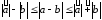 .
Проверьте их самостоятельно.
.
Проверьте их самостоятельно.
