
Материалы лекции 14
.docxЛекция 14. Гомотетия и подобие, их свойства.
Литература. [1] § 46.
Доказательство.
Пусть
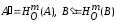 .
Тогда
.
Тогда
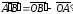 .
Из определения гомотетии, что
.
Из определения гомотетии, что
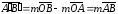 .
.
Свойство 1.
Гомотетия
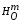 - подобие с коэффициентом
- подобие с коэффициентом
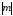 .
.
Доказательство.
Возьмем две произвольные точки А и
В. Пусть
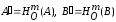 .
Из леммы следует, что
.
Из леммы следует, что
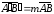 .
Поэтому
.
Поэтому
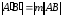 .
Свойство доказано.
.
Свойство доказано.
Свойство 2. Множество всех гомотетий с фиксированным центром образует группу преобразований.
Доказательство.
Нам достаточно доказать, что произведение
двух гомотетий и обратное преобразование
к гомотетии с центром в данной точке
также является гомотетией с тем же
центром. Пусть
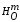 и
и
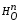 - две гомотетии с центром в точке O,
A ‑ произвольная точка плоскости.
Введем обозначения:
- две гомотетии с центром в точке O,
A ‑ произвольная точка плоскости.
Введем обозначения:
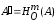 ,
,
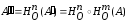 .
Из определения 2 следует, что
.
Из определения 2 следует, что
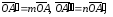 поэтому
поэтому
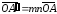 .
Таким образом, произведение
.
Таким образом, произведение
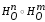 совпадает с гомотетией с центром в точке
О и коэффициентом mn:
совпадает с гомотетией с центром в точке
О и коэффициентом mn:
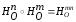 .
(1)
.
(1)
Пусть дана гомотетия
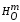 .
Рассмотрим гомотетию
.
Рассмотрим гомотетию
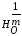 с центром в той же точек О и
коэффициентом
с центром в той же точек О и
коэффициентом
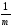 .
Тогда из доказанного соотношения (1)
получим, что произведение этих гомотетий
совпадает с гомотетией с центром в точке
О и коэффициентом 1, т.е., как отмечалось
выше, является тождественным
преобразованием. Отсюда получим:
.
Тогда из доказанного соотношения (1)
получим, что произведение этих гомотетий
совпадает с гомотетией с центром в точке
О и коэффициентом 1, т.е., как отмечалось
выше, является тождественным
преобразованием. Отсюда получим:
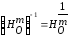 .
Свойство доказано.
.
Свойство доказано.
Рассмотрим
некоторую гомотетию с центром в точке
О и коэффициентом m. Выберем на
плоскости аффинную систему координат
так, чтобы её начало совпадало с центром
O. Пусть точка A в этой системе
имеет координаты x и y, а её образ
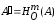 - x и y.
В силу выбора начала системы координаты
векторов
- x и y.
В силу выбора начала системы координаты
векторов
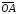 и
и
 равны:
равны:
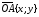 ,
,
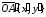 .
Так как,
.
Так как,
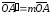 ,
то
,
то
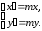 (2)
(2)
Полученные равенства представляют собой аналитическое выражение гомотетии.
Выясним, чем являются образы прямых, отрезков, лучей и углов при гомотетии.
Свойство 3. Если прямая содержит центр гомотетии, то при этой гомотетии она преобразуется сама в себя, если прямая не содержит ее центра, то она переходит в прямую, ей параллельную.
Доказательство.
Пусть дана гомотетия с центром в точке
О и коэффициентом m. Выберем
аффинную систему координат так, чтобы
её начало совпало с центром О. Тогда
аналитическое выражение гомотетии
имеет вид (2). Рассмотрим прямую l,
пусть
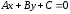 ‑ ее уравнение в этой системе
координат. Определим уравнение ее образа
‑ ее уравнение в этой системе
координат. Определим уравнение ее образа
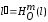 .
Для этого воспользуемся формулами (2),
выразим x и у через x
и y и подставим
полученные выражения в уравнение прямой
l:
.
Для этого воспользуемся формулами (2),
выразим x и у через x
и y и подставим
полученные выражения в уравнение прямой
l:
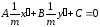 ,
или
,
или
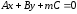 .
Если
.
Если
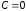 ,
то прямые l и l
совпадают друг с другом, они проходят
через центр гомотетии О. Если
,
то прямые l и l
совпадают друг с другом, они проходят
через центр гомотетии О. Если
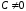 ,
то точка О не лежит на l и в этом
случае, как нетрудно видеть, прямые l
и l' параллельны между собой. Свойство
доказано.
,
то точка О не лежит на l и в этом
случае, как нетрудно видеть, прямые l
и l' параллельны между собой. Свойство
доказано.
Из этого свойства можно сделать следующий вывод: при гомотетии коллинеарные точки преобразуются в коллинеарные.
Свойство 4. При гомотетии сохраняется простое отношение трех точек.
Доказательство.
Пусть дана гомотетия
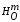 .
Рассмотрим три точки А, В и C,
принадлежащие одной прямой. Обозначим
их простое отношение (АВ,С) через
. Это означает, что
.
Рассмотрим три точки А, В и C,
принадлежащие одной прямой. Обозначим
их простое отношение (АВ,С) через
. Это означает, что
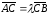 .
Пусть
.
Пусть
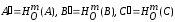 .
Точки A,
B, и С
также лежат на одной прямой и, как следует
из леммы,
.
Точки A,
B, и С
также лежат на одной прямой и, как следует
из леммы,
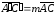 и
и
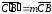 .
Поэтому
.
Поэтому
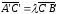 и простое отношение
и простое отношение
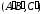 также равно . Свойство
доказано.
также равно . Свойство
доказано.
Из доказанного утверждения вытекает следующее следствие.
Свойство 5. При гомотетии отрезок преобразуется в отрезок, a луч - в луч.
При доказательстве этого свойства следует провести те же рассуждения, что и при доказательстве свойств 4 и 5 движений.
Свойство 6. При гомотетии угол преобразуется в равный ему угол.
Доказательство.
При гомотетии луч преобразуется в
луч, а коллинеарные точки – в коллинеарные.
Поэтому угол как фигура плоскости
преобразуется в угол. Следует доказать,
что образ угла по величине совпадает с
самим углом. Для этого достаточно
проверить, что их косинусы равны между
собой. Рассмотрим произвольный угол
MQN. Пусть он при
гомотетии преобразуется в угол MQN.
Выберем на сторонах угла MQN
точки А и В. Пусть
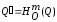 ,
,
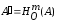 и
и
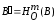 ,
тогда, как следует из следствия свойства
1,
,
тогда, как следует из следствия свойства
1,
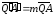 и
и
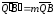 .
Так как
.
Так как
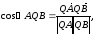
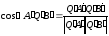 и
и
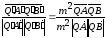 ,
то
,
то
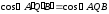 .
Свойство доказано.
.
Свойство доказано.
Применим свойства гомотетии к изучению свойств подобий общего вида.
Теорема 1.
Любое подобие p можно представить как
произведение
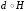 ,
где d - движение плоскости, a H - некоторая
гомотетия.
,
где d - движение плоскости, a H - некоторая
гомотетия.
Доказательство.
Пусть k - коэффициент подобия p.
Рассмотрим гомотетию
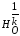 с произвольным центром О и коэффициентом
с произвольным центром О и коэффициентом
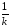 .
Легко видеть, что произведение
.
Легко видеть, что произведение
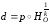 является движением. Действительно, если
A и В - две произвольны точки, то:
является движением. Действительно, если
A и В - две произвольны точки, то:
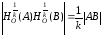 и
и
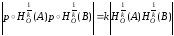 .
Отсюда следует, что
.
Отсюда следует, что
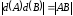 .
Преобразование
.
Преобразование
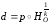 сохраняет расстояния между точками.
При доказательстве свойства 2 гомотетии
мы получили, что
сохраняет расстояния между точками.
При доказательстве свойства 2 гомотетии
мы получили, что
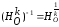 ,
поэтому
,
поэтому
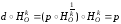 .
Теорема доказана.
.
Теорема доказана.
Из доказанной
теоремы следует, что в качестве центра
гомотетии О можно выбрать любую точку
плоскости, а её коэффициент равен
коэффициенту подобия. Легко показать,
что любое подобие можно представить
также в виде произведения
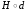 ,
где H гомотетия с
коэффициентом, равным коэффициенту
подобия, а d - некоторое
движение.
,
где H гомотетия с
коэффициентом, равным коэффициенту
подобия, а d - некоторое
движение.
С помощью теоремы 1 нетрудно выяснить, как при подобии преобразуются прямые, лучи, отрезки и углы. Действительно, как следует из свойств движения и гомотетии, при этих преобразованиях прямая, луч и отрезок преобразуются соответственно в прямую, луч и отрезок, а угол - в равный ему угол. Этому же свойству удовлетворяют образы прямых, лучей, отрезков и углов при их произведении. Таким образом, справедливо следствие теоремы 1.
Следствие. При подобии прямая преобразуется в прямую, луч ‑ в луч, отрезок ‑ в отрезок, a угол ‑ в равный ему угол.
