
Gorbachev_OsnoviTeoriiSluchajProtces[1]
.pdf
, n, t ; F(u1, t1; u2 , t2 ; ...; un , tn ) = F(ui1 , ti1 ; ui2 , ti2 , ..., uin , tin ) ,
где (i1,..., in ) – любая перестановка индексов (1, 2, …, п). Это условие вытекает из коммутативности
событий в (1.4).
Рассмотренный тип задач, в которых для описания свойств случайного процесса достаточно использование цилиндрических множеств вида (1.5), соответствует тем случаям, когда интервалы (1.4), присутствующие в моделях поведения реализаций процесса, представимы в виде
T = N ×X T \N ,
из которого следует измеримость таких интервалов и образуемых из них цилиндрических множеств. Перейдем теперь к задачам, в которых измеримость интервалов (1.4) в принятом смысле не
выполняется. К таким задачам относятся те, в которых вычисляются вероятности выполнения условий (ограничений), налагаемых на несчетное множество сечений случайного процесса.
Примером задачи такого типа является вычисление вероятности P того, что реализация случайного процесса X(t) с непрерывным аргументом на интервале времени t = [a,b) принимает значения, превышающие заданное x0:
P = P{X(t) > x0 для t [a,b)} = P( I{X (t) > x0 }). .
t [a,b)
Непосредственное вычисление этой вероятности, как вероятности конъюнкции несчетного числа событий, невыполнимо.
Исходя из следующих интуитивных соображений, можно, однако полагать, что при определенных свойствах случайного процесса задачи и приведенного типа имеют решения.
Пусть множество T значений аргумента случайного процесса X(t) непрерывно и содержит всюду плотное счетное подмножество S, а сам процесс обладает свойством стохастической непрерывности, т.е. для t T выполняется условие
P{X(t + ε) - X(t )}→0 при ε → 0.
Тогда, исследуя свойства процесса X(t), можно рассматривать его значения для дискретного множества аргумента S, т.е. вернуться к рассмотренному выше случаю, когда поведение процесса полностью описывалось системой конечномерных распределений процесса SX.
Эти соображения формализуются и подкрепляются следующими определениями и фактами, которые приводим без доказательств.
Определение 1.2. Два случайных процесса x(ω;t) и y(ω;t) стохастически эквивалентны, если для
t
P{ω: x(ω;t) = y(ω;t)} = 1.
Случайный процесс y(ω;t) называется модификацией случайного процесса x(ω;t) (и обратно). Определение 1.3. Случайный процесс x(ω;t) называется сепарабельным, если множество T
содержит всюду плотное счетное подмножество S, т.е. такое, что для любого интервала I T справедливо равенство
P{ω: sup x(ω;t) = sup x(ω;t), inf x(ω;T ) = inf x(ω;t)} =1.
t I ∩S t I t I ∩S t I
Относительно приведенных свойств случайного процесса справедливы следующие утверждения.
1.Любой случайный процесс имеет модификацию, которая является сепарабельной;
2.Если существуют a > 0, b > 0 и c < ∞ такие, что для любого t T выполняется неравенство
M x(ω;t + h) − x(ω;t) ≤ c h 1+b ,
то процесс x(ω;t) имеет стохастически непрерывную модификацию (оператор M( ) имеет здесь обычный смысл математического ожидания случайной величины Xt – сечения случайного процесса x(ω;t) при фиксированном t).
Приведенные факты подтверждают, что при определенных (достаточно широких) условиях случайный процесс с непрерывным аргументом имеет стохастически непрерывную сепарабельную модификацию, что позволяет заменить несчетное множество его аргумента T на счетное множество S и, тем самым, снять описанные выше трудности, связанные с тем, что множества, описывающие поведение случайного процесса, не являются борелевскими.
§1.2. Моментные функции случайного процесса
Свойства случайного процесса могут характеризоваться с той или иной полнотой (всегда, конечно, не большей, чем семейством S X ) так называемыми моментными функциями, являющимися
11

результатом приложения к случайным процессам понятия моментов случайных величин. К основным из них относятся функции математического ожидания, дисперсии и корреляционная функция.
Определение 1.4. Функцией математического ожидания (м.о.) mx (t) случайного процесса X(t)
называется неслучайная функция, которая для каждого значения аргумента t равна математическому ожиданию сечения процесса X(t) при данном значении аргумента, т.е.
|
|
|
|
mX (t) = MXt |
= ∫udFX (u, t) = |
|
|
|
|
|
||
|
|
|
|
|
|
|
длядискретног |
|
|
|
|
|
|
|
|
|
∑xi Pi (t) |
распределениясеченияXt ; |
|
|
|
|
(1.6) |
||
|
|
|
|
= xi N |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∞∫ufX (u, t)du |
|
длянепрерывного |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
распределениясеченияXt |
|
|
|
|
|
|
(здесь |
P (t) = P{X |
t |
= x |
} , N – множество |
значений сечения X(t), |
f |
X |
(u, t) = |
∂FX (u, t) |
– функция |
||
|
||||||||||||
|
i |
i |
|
|
|
|
|
|
∂u |
|
||
плотности распределения). |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Функция математического ожидания характеризует протекание случайного процесса «в среднем». |
||||||||||||
Определение 1.5. Функцией дисперсии |
DX (t) случайного процесса X(t) называется неслучайная |
|||||||||||
функция, которая для каждого значения аргумента t равна дисперсии сечения процесса X t при данном значении аргумента, т.е.
|
|
|
|
|
|
|
|
|
∑[xi − mx (t)]2 Pi (t) |
|
для дискретного |
|
; |
||
o |
xi N |
распределениясеченияX |
t |
||||
Dx (t) = M X t2 |
= ∫[u − mx (t)]2 dFX (u,t) = = |
|
|
|
|
(1.7) |
|
|
|
∞ |
|
|
|
|
|
|
|
∫ |
[u − mx (t)]2 f X (u,t)du |
|
|
|
|
|
|
|
для непрерывного |
||||
|
−∞ |
|
распределениясеченияX t . |
||||
Вместо функции дисперсии часто используется функция среднего квадратичного отклонения
(стандартного отклонения) σ X (t) =  DX (t) .
DX (t) .
Эти две функции характеризуют собой статистический разброс значений случайного процесса относительно функции математического ожидания, т.е. относительно его среднего значения.
Определение 1.6. Корреляционной функцией (к.ф.) RX (t1 , t2 ) случайного процесса X(t) называется неслучайная функция, которая для каждой пары значений аргументов t1 и t2 равна корреляционному моменту сечений процесса X t1 и X t2 , соответствующих этим значениям аргументов, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
o |
) =∫(u1 −mX(t1 ))(u2 −mX(t2 ))dF(u1,t1;u2,t2 ) = |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
RX(t1,t2 ) =M( Xt1 |
Xt2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i) |
|
|
|
(j) |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −m (t ))(x −m (t ))P(t ,t |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ ∑ 1 |
X 1 |
|
2 |
X 2 |
ij 1 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(i) |
|
(j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
N x |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
X |
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(длядискретнограспределениясечений X и |
|
(1.8) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ∫(u1 −mX(t1 ))(u2 −mX(t2 ))fX(u1,t1;u2,t2 )du1du2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(длянепрерывнгораспределениясеченийX и X ) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
t2 |
|
|
|
(здесь |
|
P (t ,t |
2 |
) = P{X |
t1 |
= x |
(i) , X |
t2 |
= x( j)} , |
N |
1 |
и |
N |
2 |
– множества |
значений сечений |
X |
и |
|||||||||||||
|
|
|
|
ij 1 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
t1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
X |
, |
f |
|
(u , t ;u |
|
, t |
|
) = |
|
= ∂ FX (u1, t1;u2 , t2 ) ) , |
|
|
− m (t), |
(i =1, 2) |
– центрированные |
сечения |
|||||||||||||||
X |
2 |
2 |
|
X i = X |
i |
||||||||||||||||||||||||||
|
t2 |
|
1 1 |
|
|
|
|
|
|
|
|
∂u1∂u2 |
|
|
|
|
|
|
i |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
случайного процесса).
12

Приведенное определение означает, что для каждой пары различных сечений случайного процесса значение корреляционной функции равно второму смешанному центральному моменту этих сечений, т.е. их корреляционному моменту.
Наряду с корреляционной функцией используется нормированная корреляционная функция rX (t1 ,t2 ) , которая для каждой пары аргументов t1 и t2 равна коэффициенту корреляции сечений X t1 и
X t2 : |
|
RX (t1, t2 ) |
|
|
||
rX (t1 |
, t2 ) = |
. |
(1.9) |
|||
DX (t1 )DX (t2 ) |
||||||
|
|
|
|
|||
Напомним, что из равенства Коши-Буняковского следует |
|
|
||||
| RX (t1, t2 ) | ≤ DX (t1 )DX (t2 ) |
и | rX (t1, t2 ) | ≤1 . |
(1.10) |
||||
Корреляционная и нормированная корреляционная функции характеризуют корреляционную связь между сечениями случайного процесса. Определенное преимущество второй из этих функций состоит в её безразмерности. Здесь необходимо сделать следующее терминологическое уточнение. В современной литературе функция, фигурирующая в определении 1.6. называют ковариационной функцией случайного процесса (не делая иногда различия, является ли процесс центрированным или нет). Одновременно при этом корреляционной функцией именуют функцию, названную выше нормированной корреляционной функцией. Используемая нами терминология удобна тем, что
позволяет использовать термин «ковариационная функция» для обозначения |
функции |
K X (t1, t2 ), |
равной математическому ожиданию произведения двух нецентрированных |
сечений |
случайного |
процесса: |
|
|
KX (t1,t2 ) = MXt1 Xt2 =∫u1u2dFX (u1,t1;u2 ,t2 ) = |
|
|
|
∑ ∑ x1(i) x2( j) Pij (t1,t2 ) |
|
|
|
|
x1(i) N1 x2( j) N2 |
|
|
|
для дискретного распределения сечений X |
и |
|
|
t1 |
|
|
|
= |
∞ ∞ |
|
|
∫ ∫u1u2 fX (u1,t1;u2,t2 )du1du2 |
|
−∞−∞ |
|
|
|
для непрерывного распределения сечений Xt |
|
|
||
|
|
1 |
|
|
|
Xt |
; |
2 |
(1.11) |
и Xt2.
Эта функция, представляющая собой второй смешанный начальный момент двух сечений
процесса X(t), часто будет встречаться нам в дальнейшем.
Здесь и далее мы предполагаем, что для рассматриваемых случайных процессов вводимые моментные функции существуют при всех значениях аргументов, что обеспечивается абсолютной сходимостью выражающих их рядов и интегралов. Можно, конечно, указать случаи, когда это не имеет места.
Из очевидных равенств
DX (t) = RX (t,t),
0 |
0 |
|
|
KX (t1,t2) =M((Xt |
+mX (t1))(Xt |
+mX (t2)))=RX (t1,t2)+mX (t1)mX (t2) |
(1.12) |
1 |
2 |
|
|
следует, что из рассмотренных выше моментных функций основное внимание следует уделить функции математического ожидания mX(t) и корреляционной функции RX(t1,t2) (заметим, что иногда, когда это не может вызвать недоразумений, нижние индексы в обозначениях этих моментных функций будут опускаться).
Случайные процессы, обладающие конечной моментной функцией второго порядка (т.е. корреляционной функцией RX(t1,t2)) носят название процессов второго порядка (напомним, что из существования момента r-го порядка следует существование моментов более низкого порядка; поэтому существование корреляционной функции влечет за собой существование функции математического ожидания). Изучение процессов второго порядка является содержанием корреляционной теории случайных процессов, основы которой излагаются в этой главе.
§1.3. Свойства корреляционной функции случайного процесса.
13
Многие важные свойства случайных процессов, как было сказано, могут быть получены на основе изучения свойств их функций математических ожиданий и корреляционных функций. Более того, часто эти функции вполне определяют конкретный вид семейства SX и, следовательно, полностью характеризуют свойства случайного процесса (если, конечно, априори известен тип распределений, входящих в SX) . В частности, нетрудно убедиться (см. Главу 2), что для всякого нормального (гауссовского) случайного процесса, т.е. процесса, все конечномерные распределения которого нормальны, семейство SX ={FX (u1, t1; ...; un , tn )} полностью определяется функцией математического
ожидания и корреляционной функцией.
Из определений 1.4 и 1.6 легко выводятся общие свойства функции математического ожидания mX(t) и корреляционной функции RX (t1, t2) случайного процесса X(t). Приведем ряд важных для нас свойств к.ф. RX (t1, t2) (используемые в дальнейшем свойства м.о. будут описываться по ходу изложения).
1.Ввиду неотрицательности дисперсии вещественной случайной величины имеет место соотношение
0 |
2 |
|
RX (t, t) = M X t = DX (t) ≥ 0; |
(1.13) |
|
2.Из свойства симметричности конечномерных распределений с.п. следует симметричность к.ф.:
RX (t1, t2 ) = RX (t2 , t1 ) ; |
(1.14) |
3. Пусть z = (z1,..., zn )′ – любой вещественный неслучайный вектор (n – произвольное натуральное
число); тогда |
,..., tn )′; ∑RX (ti ,t j )zi z j ≥ 0 |
(1.15) |
tr = (t1 |
||
|
n |
|
i, j=1
т. е. корреляционная функция любого случайного процесса неотрицательно определена (это следует из того факта, что при любом наборе t1,..., tn совокупность значений корреляционной функции
{R(ti ,t j )}n i, j=1 образуют корреляционную матрицу Rx случайного вектора X = ( X t1 , K, X tn , одним из
свойств которой, как известно из курса теории определенность.
В связи с этим свойством корреляционной функции нуля вектор z , для которого при некотором tr• = (t1•
вероятностей, является неотрицательная
заметим, что если существует отличный от ,..., tn• )′ неравенство (1.15) превращается в
равенство (т.е. корреляционная функция не является положительно определенной), то сечения
случайного процесса {X t• }n |
находятся в линейной зависимости, т.е. каждое из них точно |
i i=1 |
|
определяется остальными. Если это имеет место, то случайный процесс называется предсказуемым (частично предсказуемым). В противном случае (т.е. при положительной определенности корреляционной функции) процесс называется непредсказуемым (по умолчанию это более обычное свойство процесса подразумевается).
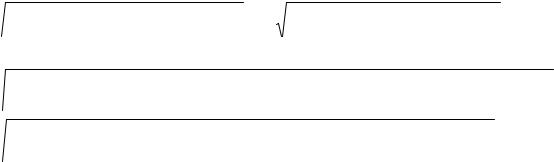
4. Из непрерывности корреляционной функции при любом t = t1 = t2 следует ее непрерывность при любых t1 и t2. Это следует из следующих соотношений, в которых используется неравенство КошиБуняковского:
14
|
RX (t1 + ε1,t2 + ε2 ) − |
RX (t1,t2 ) |
|
0 |
|
0 |
|
|
0 |
0 |
|
||||
|
=| M [ X (t1 + ε1) X (t2 |
+ ε2) − X (t1) X (t2)]|= |
|||||||||||||
|
|
0 |
0 |
|
0 |
|
|
0 |
0 |
|
|
0 |
0 |
0 |
|
= |
|
M [ X (t1 |
+ ε1) X (t2 |
+ ε2) − |
X (t1 |
+ ε1) X (t2 ) + X (t1 + |
ε1) X (t2 ) − |
X (t1) X (t2 )]|≤ |
|||||||
|
|
||||||||||||||
|
|
0 |
0 |
|
0 |
|
|
0 |
|
|
0 |
|
|
||
|
≤ |
|
M [ X (t1 + ε1)(X (t2 + ε2) − X (t2)]| + |
| M [(X (t1 |
+ ε1) − X (t1))(t2 )]|≤ |
|
|||||||||
|
|
|
|
||||||||||||
≤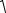 DX
DX
= DX +
DX +  DX
DX
(t |
|
0 |
|
+ |
ε |
|
0 |
|
|
)]2 + |
0 |
+ ε ) − |
0 |
|
(t |
|
) = |
|
|
+ ε )M [ X (t |
2 |
2 |
) − X (t |
2 |
M [ X (t |
X (t )]2 D |
X |
2 |
|
|
|||||||||
1 |
1 |
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||||
|
|
0 |
|
|
|
|
0 |
|
|
ε2)] − |
0 |
0 |
|
|
0 |
|
0 |
|
|
(t1 + ε1)M[ X (t2 |
+ |
ε2) X (t2 |
+ |
2M[ X (t2 |
+ ε2 ) X (t2)] + M[ X (t2) X (t2)] + |
||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
0 |
0 |
0 |
|
|
|
|
|
(t2)M[ X (t1 |
+ ε1) X (t1 + ε1)] − 2M[ X (t1 + ε1) X (t1)] + M[ X (t1) X (t1) ] →0, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε1, ε |
2 |
→ 0 |
что доказывает требуемое.
Нетрудно установить, что это свойство распространяется и на ковариационную функцию KX (t1, t2) (для этого в последнем соотношении достаточно заменить центрированные сечения случайного процесса на нецентрированные).
§1.4. Простейшие преобразования случайных процессов
Реальные случайные явления сопровождаются, как правило, видоизменениями случайных процессов при протекании их в конкретных системах и устройствах. Так, например, электрические сигналы, описываемые как случайные процессы, при прохождении через системы связи или управления могут складываться, перемножаться, дифференцироваться или интегрироваться, усиливаться или ослабляться и т.д.
В рамках корреляционной теории нас обычно интересуют те преобразования, которым подвергаются при этом моментные функции случайных процессов – математическое ожидание и корреляционная функция. Для исследования этого вопроса нам потребуется еще одна характеристика, относящаяся к двум случайным процессам, определенным на общем вероятностном пространстве.
Определение 1.7. Взаимной корреляционной функцией R XY (t1 , t 2 ) случайных процессов X(t) и Y(t), определенным на общем вероятностном пространстве, называется неслучайная функция RXY, которая для каждой пары значений аргументов t1 и t2 равна корреляционному моменту сечений X t1 и
Yt2 этих процессов, т.е.
|
|
|
o |
o |
0 0 |
|
RXY (t1 ,t2 |
) = M X t1 |
Y t2 |
= ∫x y dF(x, t1 ; y,t2 |
) = |
||
|
∑ ∑(xi − m X (t1 |
))(y j − mY (t2 ))Pij (t1 |
,t2 ) |
|||
xi N1 y j N 2 |
|
|
|
|||
|
|
|
|
распределе ния; |
(1.16) |
|
для дискретног о |
||||||
= |
∞ ∞ |
|
|
|
|
|
|
∫ ∫ |
|
− m X (t1 ))(y − mY (t2 ))f(x, t1 ; y,t2 )dxdy |
|||
|
|
(x |
||||
−∞−∞
для непрерывно го распределе ния
15
(здесь |
N1 |
и |
N |
2 |
|
– |
множество |
значений |
сечений |
X t |
и |
Yt |
, |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
Pij (t1, t2 ) = P{X (t1 ) = xi , Y (t2 ) = y j }, F(x, t1; y, t2 ), f (x, t1; y, t2 ) –функция и плотность |
совместного |
||||||||||||
распределения сечений |
X t |
и Yt |
2 |
). |
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Ясно, что, вообще говоря, RXY (t1, t2 ) ≠ RXY (t2 , t1 ) , но RXY (t1, t2 ) = RYX (t2 , t1 ) . |
|
|
|
|
|||||||||
Функция |
RXY (t1, t2 ) |
описывает корреляционную связь между значениями случайных процессов |
|||||||||||
X(t) и Y(t) в различные моменты времени. Примером такой связи является связь между положением самолета вдоль вертикальной оси в момент t2 и силой вертикального порыва ветра в момент t1 < t2, проявляющаяся с некоторым запаздыванием t2 – t1, зависящим от инерции самолета.
Перейдем к рассмотрению простейших видов преобразований случайных процессов.
Преобразование вида Y(t) = a(t)X(t) |
+ b(t). |
Здесь X(t) – «входной» случайный процесс, |
обладающий математическим ожиданием |
mX(t) |
и корреляционной функциейRX (t1 ,t2 ) , Y(t) – |
«выходной» (преобразованный) случайный процесс, a(t), b(t) – ограниченные неслучайные функции. Из свойств математического ожидания следует:
mY (t) = MY (t) = M [a(t) X (t) + b(t)] = a(t)mX (t) + b(t) . |
(1.17) |
|
|
Для корреляционной функции Ry (t1, t2 ) и дисперсии Dy (t) |
получим: |
|
|
RY (t1 , t2 ) = M Yo (t1 ) Yo (t2 ) = a (t1 )a (t2 ) R X (t1 , t2 ) ; |
(1.18) |
|
|
DY (t ) = R Y (t, t ) = a 2 (t ) D X (t ) . |
(1.19) |
||
n |
|
|
|
Преобразование вида Y (t) = ∑ai (t) X i (t) . Здесь {X i (t)}in=1 |
– совокупность случайных процессов, |
||
i=1
определенных на общем вероятностном пространстве и обладающих математическими ожиданиями
{m |
x |
(t)}n |
, |
корреляционными функциями {R |
x |
(t , t |
2 |
)}n |
и взаимными корреляционными функциями |
|||||||||
|
i=1 |
|
|
|
|
|
|
|
1 |
|
i=1 |
|
|
|
|
|||
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
{R |
|
(t , t |
2 |
)}n |
, {a |
(t)}n |
|
– неслучайные ограниченные функции. |
|
|
|
|||||||
|
Xi X j 1 |
|
i, j=1 |
i |
i=1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Нетрудно убедиться, что |
|
n |
|
|
|
n |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
m Y ( t ) = |
M ( ∑ a i ( t ) X i ( t )) |
= ∑ a i ( t ) m X i ( t ) ; |
(1.20) |
||||||
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
i =1 |
|
|
||
|
|
|
|
|
|
|
|
|
n |
|
|
|
o |
|
n |
o |
|
|
|
|
|
|
|
|
|
RY (t1 , t2 ) = M ∑ ai (t1 ) X i (t1 )∑ a j (t2 ) X j (t2 ) |
= |
|
|||||||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
(1.21) |
|
|
|
|
|
|
|
= ∑ ai (t)ai (t2 )RX i |
(t1 , t2 ) + ∑ ai (t1 )a j (t2 )RX i X j (t1 , t2 ), |
|
|||||||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
i, j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i≠ j ) |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
DY (t ) = ∑ a i2 |
(t ) D X i |
(t ) + ∑ ai (t )a j (t ) R X i X j |
(t, t ) |
(1.22) |
|||||
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
i , j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( i ≠ j ) |
|
|
|
(в (1.20), (1.21) операция математического ожидания выполняется по совместному распределению
сечений {X |
i |
(t)}n |
). |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
X i (t) |
|
|
|
|
|
Если |
|
случайные |
процессы |
взаимно |
некоррелированы, |
т.е. |
||||
i, j (i ≠ j), t1 ,t2 ; RXi X j (t1 ,t2 ) = 0 , то |
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
RY (t1 ,t2 ) = ∑ai (t1 )ai (t2 )RXi |
(t1 ,t2 ) ; |
|
(1.23) |
|||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
DY (t) = ∑ai2 (t) DX i (t) . |
|
(1.24) |
||
|
|
|
|
|
|
i=1 |
|
|
|
|
Если i; ai (t) ≡1 , то (1.23) и (1.24) принимают вид |
|
|
|
|
||||||
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
DY (t) = ∑DX i (t) + |
∑RXi X j |
(t1,t2 ) ; |
|
(1.25) |
|
|
|
|
|
|
|
i=1 |
i, j=1 |
|
|
|
|
|
|
|
|
|
|
(i≠ j) |
|
|
|
16

n
DY (t) = ∑DX i (t) . (1.26)
i=1
В электрофизических приложениях дисперсия случайного сигнала пропорциональна средней мгновенной мощности его переменной составляющей. Поэтому (1.26) выражает тот известный факт, что при сложении независимых (некогерентных) сигналов их средние мгновенные мощности складываются. При суммировании когерентных сигналов имеет место их взаимное усиление и ослабление, выражаемое членами, содержащими взаимные корреляционные функции в (1.25).
§1.5. Дифференцирование и интегрирование случайных процессов
Дифференцирование и интегрирование случайного процесса происходит, например, при его прохождении через дифференцирующую или интегрирующую цепь в системе автоматического управления.
Чтобы определить корректно понятие производной и интеграла от случайного процесса, необходимо использовать понятие сходимости последовательности случайных величин. Из теории вероятности нам известно по крайней мере четыре типа такой сходимости: по распределению, по вероятности, с вероятностью единица (почти наверное) и в среднем квадратичном. Выбор типа сходимости зависит от содержания решаемой задачи. Так, если в задаче исследуется поведение отдельной траектории (реализаций) процесса (например, динамика изменения какого либо экономического параметра отдельного предприятия), то естественно использовать для этой цели сходимость с вероятностью единица. В тех же случаях, когда исследователя интересует коллективное поведение траекторий процесса (конкретно –средний по их множеству квадрат отклонения от предполагаемого предела), то следует применять сходимость в среднем квадратичном. Известно, что эти типы сходимости не находятся в импликативном отношении: из первого типа сходимости не следует второй, и наоборот. Читателю полезно вспомнить контрпримеры, доказывающие этот факт. Напомним также, что каждый из этих типов сходимости влечет за собой сходимость по вероятности, из которой, в свою очередь, следует сходимость по распределению.
Далее мы будем использовать сходимость в среднем квадратичном (тех, кто интересуется моделями случайных процессов с применением сходимости с вероятностью единица, мы отсылаем к
[2]).
Итак, рассматривается сходимость последовательности |
случайных величин {X |
}∞ |
к случайной (в |
||
общем случае) величине Х в среднем квадратичном («в с.к.»), т.е. такая, что |
n n=1 |
|
|||
|
|
||||
lim M ( X n − X )2 |
= 0 . |
|
|
||
n→∞ |
|
|
|
|
|
Для такого типа сходимости используются обозначения |
|
|
|
||
с.к. |
или |
l.i.m X n = X . |
|
|
|
X n → X |
|
|
|||
|
|
n→∞ |
|
|
|
Далее нам потребуются следующие леммы, описывающие свойства этого типа сходимости
последовательности случайных величин. |
|
|
|
|
|
|
|
|
|
|
|||
Лемма 1.1. Пусть {X |
m |
}∞ |
, {Y }∞ |
|
, X |
и Y |
– |
случайные |
величины, заданные на одном |
||||
|
m =1 |
n n=1 |
|
|
|
|
|
|
|
|
|
||
вероятностном пространстве, и |
с.к. |
|
|
с.к. |
|
|
|
|
|
|
|
||
|
|
|
|
Yn |
, |
MX |
2 |
< ∞, |
MY |
2 |
< ∞. |
||
Тогда |
X m → X , |
|
→Y |
|
|
||||||||
|
|
lim MX Y = M l.i.m X |
l.i.mY = MXY . |
|
|||||||||
|
|
|
|
||||||||||
|
|
m,n→∞ |
m n |
m→∞ |
|
m n→∞ |
n |
|
|
|
|||
Справедливость этой леммы вытекает из соотношений:
X mYn − XY = ( X m − X )(Yn −Y ) + ( X m − X )Y + (Yn −Y ) X ;
| MX mYn − MXY | ≤
≤ | M ( X m − X )(Yn −Y ) | + M ( X m − X )Y + | M (Yn −Y ) X | .
Применяя неравенство Коши-Буняковского и используя уcловия леммы, при m,n → ∞ получим: | M ( X m − X )(Yn −Y ) | ≤  M ( X m − X )2 M (Yn −Y )2 → 0;
M ( X m − X )2 M (Yn −Y )2 → 0;
| M ( X m − X )Y | ≤  M ( X m − X )2 MY 2 → 0;
M ( X m − X )2 MY 2 → 0;
| M (Yn −Y ) X | ≤  M (Yn −Y )2 MX 2 → 0;
M (Yn −Y )2 MX 2 → 0;
отсюда
17
|
lim |
MX m Y n = MXY . |
|
m , n → ∞ |
|
Следствие. Полагая Yn ≡Y ≡1 , получим |
|
|
lim |
MX m |
= M l.i.m X m = MX . |
m → ∞ |
|
m → ∞ |
Лемма 1.2. Сходимость в среднем квадратичном обладает свойством фундаментальности по Коши
в следующей форме. Пусть {X |
}∞ |
|
– последовательность случайных величин, для каждой из которых |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MX k2 < ∞ . Необходимым |
|
и |
|
достаточным |
|
|
условием |
|
сходимости |
в |
|
среднем |
квадратичном |
||||||||||||||||||||||||
последовательности {X |
|
}∞ |
|
к некоторой случайной величине Х с MX 2 < ∞ является равенство |
|
|
|||||||||||||||||||||||||||||||
|
|
|
k k=1 |
|
|
|
|
|
|
|
lim M (Ym − Zn )2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m,n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
для любых двух подпоследовательностей {Y }∞ |
|
|
и {Z |
n |
}∞ |
последовательности {X |
}∞ |
({Y } {X |
k |
} , |
|||||||||||||||||||||||||||
{Zn } {X k } ). |
|
|
|
|
|
|
|
|
|
|
|
m m =1 |
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
k k =1 |
|
|
m |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство этой леммы опускаем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Лемма 1.3. |
{Y }∞ |
|
|
{Z |
|
}∞ |
|
любые подпоследовательности последовательности { X |
|
} . Тогда |
|
||||||||||||||||||||||||||
Пусть снова |
|
и |
n |
|
k |
|
|||||||||||||||||||||||||||||||
|
|
m m =1 |
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) если Y |
|
с.к. |
|
|
X , |
Z |
|
|
|
с.к. |
|
|
|
|
|
|
|
|
|
|
|
то MY |
|
Z |
|
|
→ MX 2 |
|
< ∞ ; |
|
|
||||||
m |
→ |
|
→ X, MX 2 < ∞, |
m |
n |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с.к. |
|
|
|
|
|
|
|
|
|
|
|||||
б) если MY m Z n → c, | |
c |< ∞, |
|
|
|
|
: X k |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
то X |
|
|
|
→ X , |
|
MX |
|
< ∞ . |
|
|
|
|
|
||||||||||||||||||||||||
Первая часть леммы непосредственно следует из леммы 1.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Далее, из равенств |
|
|
|
|
|
|
|
|
|
|
) 2 = Y |
|
2 |
|
|
|
|
|
|
+ Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(Y |
m |
− Z |
n |
|
− 2Y |
m |
Z |
n |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
lim M (Y |
m |
− Z |
n |
) 2 = c − 2c + c = 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
с учетом леммы 1.2 следует |
|
|
|
|
|
с.к. |
|
|
MX |
2 |
< ∞, т.е. справедливость второй части леммы. |
|
|
||||||||||||||||||||||||
|
X k → X , |
|
|
|
|||||||||||||||||||||||||||||||||
Роль элементов последовательностей с.в., фигурирующих в приведенных леммах, будут играть сечения исследуемого случайного процесса; счетные множества сечений процесса упорядочены в леммах целочисленными индексами.
Теперь можно ввести понятие непрерывности случайного процесса второго порядка в среднем квадратичном.
Определение 1.8. Случайный процесс второго порядка непрерывен в среднем квадратичном при значении аргумента t, если выполнено условие
с.к. |
(1.27) |
X (t + ε) → X (t ). |
ε→ 0
Определение 1.9. Случайный процесс второго порядка непрерывен в среднем квадратичном, если (1.27) выполняется для всех t T .
Непрерывность случайного процесса в среднем квадратичном, по сути, означает, что среднее значение квадрата разности двух сечений случайного процесса стремится к нулю по мере сближения этих сечений.
Так как сходимость в среднем квадратичном влечет за собой сходимость по вероятности, то для непрерывного в среднем квадратичном случайного процесса выполняется условие:
t T , δ > 0 , lim P {| X ( t + ε) − X ( t ) |< δ} = 1,
ε → 0
т.е. вероятность реализации случайного процесса, для которой расхождение ее значений для двух близких сечений X t и X t+ε не превышает заданной величины δ, стремится к единице по мере
сближения этих сечений процесса.
Заметим, что это свойство случайного процесса вовсе не означает непрерывность его реализаций: последнее осуществляется (с вероятностью единица), если элементыω множества исходов Ω, для которых реализации x(ω;t) процесса X(t) непрерывны для всех t, образуют множество A, вероятностная мера которого равна единице, т.е.
18

P ( A) = P{ω : lim x(ω; t + ε) = x(ω; t ) для всех t } = 1 .
ε→0
Такое определение непрерывности случайного процесса основано на сходимости с вероятностью единица, которая, однако, не следует из сходимости в с.к. (вскоре мы встретимся с случайным процессом, все реализации которого разрывны, что не мешает ему быть непрерывным в с.к.).
Продолжим рассмотрение непрерывности случайных процессов в с.к. Справедлива следующая теорема.
Теорема 1.1. Необходимым и достаточным условием непрерывности случайного процесса Х(t) в
среднем квадратичном |
при значении |
|
аргумента |
t |
является |
непрерывность при t1 = t2 = t |
||||||||||
ковариационной функции K(t1,t2 ) , |
|
определенной (1.11), или, что то же, непрерывность |
||||||||||||||
математического ожидания т(t) и корреляционной функции R ( t 1 , t 2 ) |
случайного процесса Х(t). |
|||||||||||||||
Достаточность следует из следующих соотношений: |
|
|
|
|
|
|
|
|
||||||||
M [ X ( t + ε ) − X ( t )] 2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= MX ( t + ε ) X ( t + ε ) − 2 MX ( t + ε ) X ( t ) + MX ( t ) X ( t ) = |
|
|||||||||||||||
= K ( t + ε, t + ε ) − 2 K ( t + ε, t ) + K ( t , t ) → 0 |
при |
|
ε → 0. |
|
|
|
||||||||||
Для доказательства необходимости привлечем лемму 1.3а. Поскольку при ε1,ε2 → 0 |
||||||||||||||||
|
|
X ( t + ε |
|
с. к. |
→ X ( t ), |
|
|
|
|
|
|
|
||||
|
|
1 ) |
|
|
|
|
|
|
|
|||||||
|
|
X ( t + ε |
|
с. к. |
→ X ( t ), MX |
2 |
( t ) < ∞ , |
|
||||||||
то |
|
2 ) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MX |
(t + ε ) X (t + ε |
2 |
) → MX 2 (t) |
, т.е. K(t + ε , t + ε |
2 |
) → K(t, t). |
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
||
Из (1.12) ясно, что для непрерывности K(t1, t2 ) |
при t = t1 = t2 |
достаточная непрерывность в этой |
||||||||||||||
точке R(t1 ,t2 ) и m(t) . Обратно, из непрерывности K(t1, t2 ) |
следует, что |
|
||||||||||||||
lim |
M [ X (t + ε) − X (t )] 2 = |
|
|
|
|
|
|
|
|
|
||||||
ε→ 0 |
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
||
= lim |
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M [ X (t + ε) |
− X (t ) + m (t + ε) − m (t )] 2 = |
|
|
|
||||||||||||
ε→ 0 |
o |
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
2 + lim [m (t + ε) − m (t )] 2 |
= 0. |
||||||||||||
M [ X (t + ε) |
− X (t )] |
|||||||||||||||
ε→ 0 |
|
|
|
|
|
|
ε→ 0 |
|
|
|
|
|
|
|
||
Последнее равенство означает, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
|
o |
o |
|
|
|
lim [ m ( t + ε) − m ( t )] 2 |
= 0 . |
||||||||
M [ X ( t + ε) − |
X ( t )] 2 = 0 и |
|||||||||||||||
ε → 0 |
|
|
|
|
|
|
|
ε → 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Первое из этих равенств влечет за собой, в силу доказанного, непрерывность RX (t1, t2 ) = K o (t1, t2 )
X
в точке t1 = t2 = t , что и завершает доказательство теоремы.
Производная с.п. в среднем квадратичном. Теперь мы можем ввести понятия производной и дифференцируемости случайного процесса в среднем квадратичном смысле.
Определение 1.10. Производной X ′(t) случайного процесса второго порядка Х(t) в среднем
квадратичном в точке t называется предел |
dX (t ) |
|
X (t + ε) − X (t ) |
|
|
X ′(t ) = |
= l.i.m |
(1.28) |
|||
dt |
ε |
||||
|
ε→ 0 |
|
(если он существует).
Определение 1.11. Случайный процесс второго порядка Х(t) является дифференцируемым в среднем квадратичном в точке t, если в этой точке существует предел (1.28).
Если (1.28) выполняется при всех t (t1, t2 ) , то случайный процесс дифференцируем в среднем квадратичном на интервале (t1, t2 ) .
Справедлива следующая теорема.
Теорема 1.2. Необходимым и достаточным условием существования в точке t производной в среднем квадратичном c ограниченным моментом второго порядка случайного процесса второго порядка Х(t) является существование производной
19
|
|
|
|
|
|
|
|
|
|
∂ 2 K X (t1 , t2 ) |
|
|
|
|
= c < ∞ . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂t1∂t2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 = t 2 = t |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для доказательства этой теоремы положим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Z k (t1 ) = |
X (t1 + k ) − X (t1 ) |
, |
|
|
Z l |
(t2 ) = |
X (t2 + l ) − X (t2 ) |
, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
l |
|||
где k и l – произвольные числа. Справедливо равенство |
|
|
|
|
|||||||||||||||||||||
M (Z |
k |
(t )Z |
(t |
2 |
)) = |
K X (t1 + k, t2 +l) − K X (t1 + k, t2 ) − K X (t1 , t2 +l) + K X (t1 , t2 ) |
. |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
1 |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
∂2 K |
X |
(t , t |
2 |
) |
|
|
|
|
|
||||
|
|
|
|
|
Из существования |
|
|
|
1 |
|
|
|
|
|
= c < ∞ следует, что |
||||||||||
|
|
|
|
|
|
∂t1∂t2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 = t 2 =t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
k , l → 0 |
|
lim M [ Z k (t1 ) Z l ( t2 )] = c , | c |< ∞ , |
||||||||||||||||
или, ввиду леммы 1.3б, |
|
|
|
|
|
|
|
|
Z l (t) = Z (t ) = X ′(t ) (достаточность). |
||||||||||||||||
Z (t ) : М [Z (t)]2 < ∞ : l.i.m |
Z k |
(t) = l.i.m |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
k →0 |
|
|
|
|
|
l →0 |
|
|
|
|
|
|
|
|
|
||
Если при k → 0 |
|
|
с.к. |
|
|
|
′ |
|
|
|
|
|
|
|
|
2 |
< ∞ , то, согласно лемме 1.3а, |
||||||||
|
Z k (t) → Z (t) |
= X (t), M [Z (t)] |
|
||||||||||||||||||||||
|
|
lim |
|
|
|
|
|
|
2 |
K X (t1 , t2 ) |
|
|
|
|
|
|
= M [ Z (t )] 2 < ∞ (необходимость). |
||||||||
|
|
MZ k (t ) Z l (t ) = ∂ |
|
|
|
|
|
|
|
||||||||||||||||
|
|
k , l → 0 |
|
|
|
|
|
|
|
∂t, ∂t2 |
|
|
t1 = t 2 = t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нетрудно показать, что и здесь, как и в теореме 1.1, условие существования ограниченной второй
производной ковариационной функции |
K X ( t1 , t2 ) может быть заменено условием существования у |
||||||||||
случайного процесса X (t ) |
|
ограниченных производных математического ожидания |
dm X |
(t ) |
и |
||||||
|
dt |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
R X (t1 , t2 ) |
|
|
. |
|
|
|
||
корреляционной функции |
|
|
|
|
|
|
|||||
|
|
|
∂t |
∂t |
2 |
t |
=t |
=t |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
Если условия теоремы выполнены для t T , то в результате дифференцирования в среднем квадратичном случайного процесса второго порядка Х(t) возникает процесс X′(t) также второго порядка. Найдем в этих условиях математическое ожидание и корреляционную функцию случайного
процесса X ′(t) = |
dX (t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя следствие леммы 1.1, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X (t + ε) − X (t) |
|
|
|
||||||||||||||||
|
|
|
|
mx′ (t) = MX ′(t) = M l.i.m |
|
|
= |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε→0 |
|
|
|
|
|
|
|
|
|
|
|
|
(1.29) |
||||||
|
|
|
|
|
|
M ( X (t + ε) − X (t)) |
|
|
|
dm x (t) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
= lim |
= |
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Далее, лемма 1.1 дает |
ε→ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
o |
|
o |
|
|||
Rx′ (t1 ,t2 ) = M X '(t1 ) X '(t2 ) = M l.i.m X (t1 + k) − X (t1 ) l.i.m X (t2 |
+ l) − X (t2 ) = |
|
||||||||||||||||||||||||||||||||
|
|
|
o |
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k →0 |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
l→0 |
|
l |
|
(1.30) |
||||
|
o |
|
o |
o |
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)] |
|
|
|
∂2 R |
|
(t |
,t |
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||
= lim M |
[ X (t |
1 |
+ k) − X (t |
)][ X (t |
2 |
+ l) − X (t |
2 |
|
= |
X |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
k ,l→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t1∂t2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D x′ (t) = |
|
|
2 |
R X |
(t1 , t |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∂ |
|
2 ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂t , ∂t |
2 |
|
|
|
t |
=t |
=t |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
Нетрудно найти выражение для взаимной корреляционной функции случайного процесса X (t) и его производной X ′(t) :
20
