Интегрирование по частям.

Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения и последующем применении формулы. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.

Пример.

Вычислить неопределенный интеграл .

Решение.

Пусть , тогда

Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.

Теперь применяем формулу интегрирования по частям:

Последний интеграл вычислим по методу подведения под знак дифференциала.

Так как , то. Поэтому

Следовательно, где

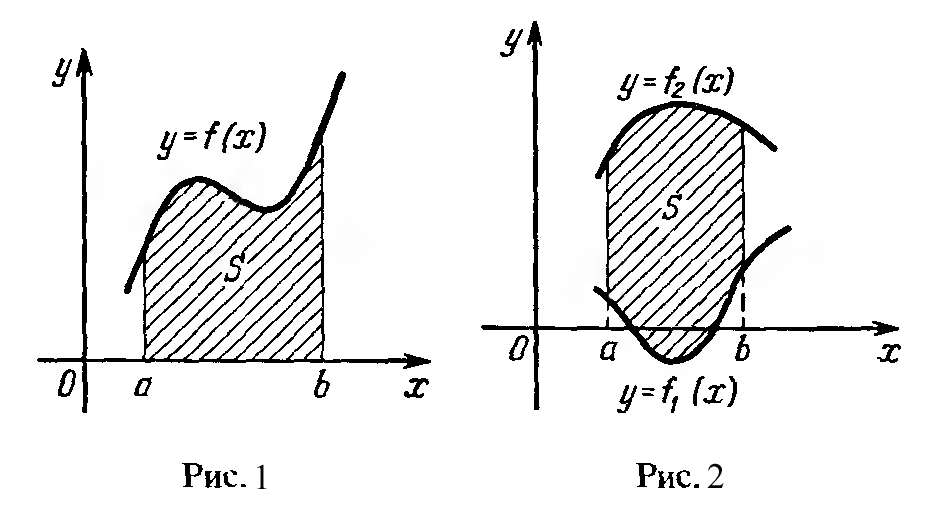
44. Площадь плоской фигуры.

Площадь фигуры, ограниченной графиком непрерывной функции y=f(x)(f(x)≥0),  двумя прямыми x=a  и x=b  и осью Ox,  или площадь криволинейной трапеции, ограниченной дугой графика функции y=f(x),a≤x≤b  (рис. 1) вычисляется по формуле

S=∫ a b f(x)dx. 

Площадь фигуры, ограниченной графиками непрерывных функций y=f 1 (x)  и y=f 2 (x),f 1 (x)≤f 2 (x)  и двумя прямыми x=a  , x=b  (рис. 2) определяется по формуле S=∫ a b (f 2 (x)−f 1 (x))dx. 

Если фигура ограничена кривой, имеющей параметрические уравнения x=x(t),y=y(t),  прямыми x=a,x=b  и осью Ox,  то площадь ее вычисляется по формуле

S=∫ t 1  t 2  y(t)x ′ (t)dt=∫ t 1  t 2  y(t)dx(t),(1) 

где пределы интегрирования находятся из уравнений a=x(t 1 ),b=x(t 2 )  (y(t)≥0  на отрезке [t 1 ,t 2 ]  ).

Формула (1) применима также для вычисления площади фигуры, ограниченной замкнутой кривой (изменение параметра t  от t 1   до t 2   должно соответствовать обходу контура по часовой стрелке).

Площадь фигуры, ограниченной графиком непрерывной функции r=r(φ)  и двумя лучами φ=α,  φ=β,  где φ  и r−  полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции, r=r(φ),α≤φ≤β,  вычисляется по формуле

S=12 ∫ α β r 2 dφ. 

47.Существование и единственность решения

Обыкновенное дифференциальное уравнение первого порядка, разрешённое относительно производной, имеет вид

(8.1)

Решением обыкновенного дифференциального уравнения (8.1) называется функция , подстановка которой в уравнение обращает его в тождество:

.

График решения называется интегральной кривой.

Задача Коши для дифференциального уравнения (8.1) состоит в том, чтобы найти решение уравнения (8.1), удовлетворяющее начальному условию

                                                       .                                               (8.2)

Пару чисел называют начальными данными. Решение задачи Коши называется частным решением дифференциального уравнения (8.1) при условии (8.2).

Частному решению соответствует одна из интегральных кривых, проходящая через точку .

Условия существования и единственности решения задачи Коши содержатся в следующей теореме.

Теорема 8.1. Пусть функция − правая часть дифференциального уравнения (8.1) – непрерывна вместе со своей частной производнойв некоторой областина плоскости. Тогда при любых начальных данныхзадача Коши (8.1), (8.2) имеет единственное решение.

При выполнении условий теоремы через точку на плоскости проходит единственная интегральная кривая. Будем считать, что условия теоремы существования и единственности выполняются.

Численное решение задачи Коши (8.1), (8.2) состоит в том, чтобы получить искомое решение в виде таблицы его приближённых значений для заданных значений аргументана некотором отрезке:

                                           (8.3)

Точки (8.3) называют узловыми точками, а множество этих точек называют сеткой на отрезке . Будем использовать равномерную сетку с шагом:

;

или 

Приближённые значения численного решения задачи Коши в узловых точках обозначимчерез .