Непрерывность ф-ции, имеющей производную.

Предложение 1. Для того,чтобы ф-ция f(x) была непрерывна в точке х, необходимо и достаточно, чтобы (Данная запись называетсяразностной формой усл-я непрерывности).

Д-во: 1)[Необходимость]

2)[Достаточность] =0

Функция y=f(x) называется дифференцируемой в точке х, если её приращение в этой точке, соответствующее приращению аргумента , имеет следующий вид:(1), где А — постоянная, не зависящая от, a- бесконечно малая ф-ция при.

, тогда (1) запишется в виде при

Теорема 1. Чтобы ф-ция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она в этой точке имела производную .

Док-во: 1) [Необходимость]. Ф-ция дифференцируема, значит . Разделим обе части этого выражения наи получим. Так как- б.м.ф-ция, то=A

2)[Достаточность] Предел сущ-ет, значит . По определению,, преобразуем и получаем.

Замечание. А=в точкех.

Дифференцирование — операция взятия производной.

Теорема 2. Если ф-ция f(x) дифференцируема в точке х то она непрерывна в этой точке.

Док-во: . Так как- б.м.ф-ция, то. Тогда попредложению 1, функция непрерывна.

30

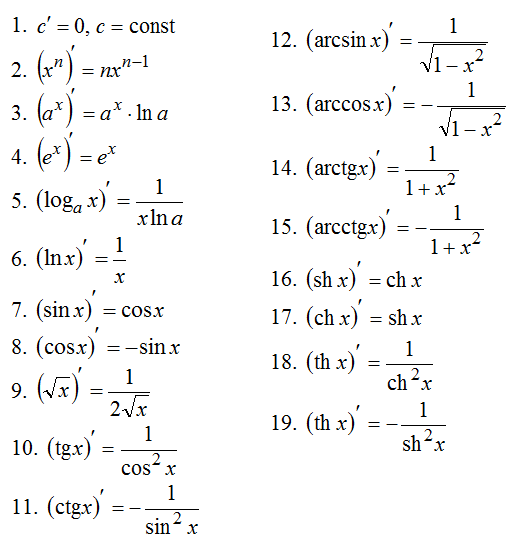
34. Чтобы найти наибольшее или наименьшее значение функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим  производную функции

3. Приравниваем производную  к нулю

4. Находим промежутки, на которых производная сохраняет знак,  и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции , то функциявозрастает на этом  промежутке.

Если на промежутке I производная функции , то функцияубывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-».

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

• затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции

• или   сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

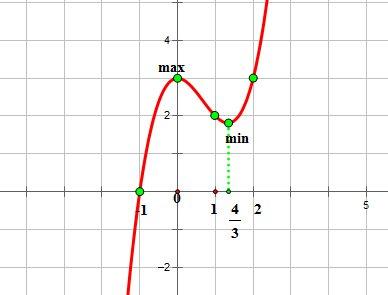В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее – в левом:.

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее – в одном из концов отрезка, то есть надо найти значенияии выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то естьи.

Чтобы найти наименьшее значение функции,  нам нужно будет сравнить значения функции в точке минимума  и в левом конце отрезка, то есть и.

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции – множество действительных чисел.

2. 

3. , еслиили

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:

 

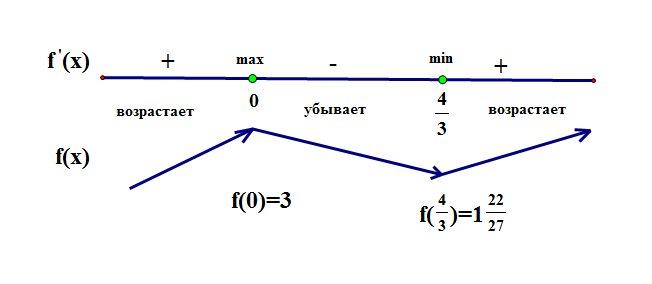
35. График функции , дифференцируемой на интервале, является на этом интервалевыпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале, является на этом интервалевогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

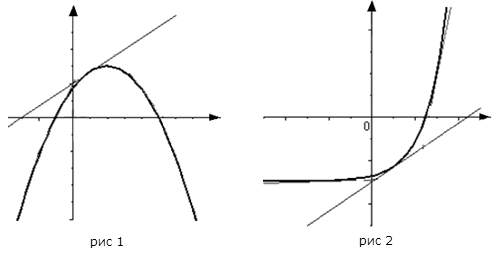
Точки, которые разделяют промежутки выпуклости и вогнутости называются точками перегиба функции.

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция определена на интервалеи имеет непрерывную, не равную нулю в точкевторую производную. Тогда, есливсюду на интервале, то функция имеетвогнутость на этом интервале, если , то функция имеетвыпуклость.

Определение

Точкой перегиба графика функции называется точка, разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция имеет перегиб в точке, тоили не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

1. первая производная 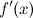непрерывна в окрестности точки ;

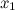2. вторая производная 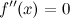или не существует в точке;

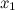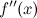3. при переходе через точку 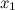меняет свой знак,

тогда в точке функцияимеет перегиб.

Схема исследования функции на выпуклость, вогнутость

1. Найти вторую производную функции.

2. Найти точки, в которых вторая производная равна нулю или не существует.

3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

36. Точка называется критической точкой второго рода, если 1. непрерывна в некоторой окрестности ; 2. существует (конечная или бесконечная) производная функции в точке ; 3. дважды дифференцируема в некоторой проколотой окрестности точки ; 4. вторая производная этой функции в точке равна нулю или не существует. В общем-то Марго права: Критическая точка второго рода - это точка функции, в которой вторая производная функции равна 0. В этой точке происходит перегиб, то есть график меняется с выпуклого вверх на выпуклый вниз, или наоборот