17. Кривые второго порядка

Общий вид линии второго порядка:

. (1)

К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.

1. Окружность

Окружность – это множество точек плоскости, равноудаленных от данной точки (центра).

(2)

где - радиус окружности,и- координаты центра окружности.

Если центр окружности совпадает с началом координат, то уравнение имеет вид

(3)

Рис. 2

2. Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами).

Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках и:

(4)

где и- полуоси эллипса, с – полуфокусное расстояние. Коэффициентыэллипса связаны соотношением

Рис. 3

Если центр эллипса находится в точке , то уравнение эллипса имеет вид:

(5)

3. Гипербола

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Уравнение гиперболы с центром в начале координат и с фокусами в точках иимеет вид:

(6)

где - действительная полуось,

- мнимая полуось.

Коэффициенты игиперболы связаны соотношением.

Прямые - асимптоты гиперболы.

Рис. 4

Если центр гиперболы находится в точке , то уравнение имеет вид:

(7)

4. Парабола

Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.

Уравнение параболы с вершиной в начале координат имеет вид:

, (8)

где - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты.

Рис. 5

Если вершина параболы находится в точке , то уравнение имеет вид:

(9)

Задача 1.Составить уравнение геометрического места точек, равноотстоящего от осиОуи точки.

Решение:Возьмем на искомой линии произвольную точку. Расстояние точкиМот точкиFопределится по формуле расстояния между двумя точками:

Расстояние точки Мдо осиОуопределится:

Так как по условию , то искомая кривая имеет уравнение:

Линия, определяемая полученным уравнением является параболой.

Задача 2.Составить уравнение геометрического места точек, отношение расстояний которых до точкиF(-1; 0) и до прямой х = -9 равно 1/3.

Решение:Возьмём на искомой кривой произвольную точку. Её расстояния от точкии прямой составляют

Из условия задачи следует:

Таким образом, искомая кривая имеет уравнение:

Приведём это уравнение к каноническому виду:

- это уравнение эллипса с полуосями:

 

1. Основные формулы в декартовых прямоугольных координатах

     При решении задач аналитической геометрии будем использовать действия над векторами, заданными в координатной форме.      Пусть даны векторы и. Тогда:      1) при сложении (вычитании) векторовполучим вектор;      2) при умножении векторана число λ получим вектор;      3) при скалярном произведении векторовполучим число.Расстояние между двумя точками      Даны точки А (x_A, y_A) и В (x_В, y_В). Расстояние между ними найдем, как длину вектора = (x_В – x_А, y_B - y_A). Из скалярного произведения имеем. Подсчитав скалярное произведение через координаты вектора, получаем расстояние между двумя точками.                                  (1)Угол между двумя векторами      Даны два вектора: и. Косинус угла между ними:.                            (2)Деление отрезка в заданном отношении      Пусть даны точки А (x_А y _А), и В (x_В y _В ). Требуется найти координаты точки С (x, y ) , делящей отрезок  АВ в заданном отношении λ:     

В      A                           С

.

     Для решения задачи воспользуемся действием умножения вектора на число. Перепишем отношение  в виде: |AC|=λ| CB|. Такое соотношение длин может быть получено при выполнении действия .      В равных векторах равны соответствующие координаты:.      Из этих уравнений найдем неизвестные координаты точки С:.                                    (3)      В частности, для середины имееми поэтому λ=1. Следовательно, координаты середины отрезка находятся по формулам:(4)Условия параллельности и перпендикулярности векторов      Так как скалярное произведение двух перпендикулярных векторов иравно 0, то условием перпендикулярности отличных от нуля векторов будет равенство.      При умножении векторана скалярполучаем вектородного направления спри λ > 0и противоположного направления при λ < 0. Но всегда векторыбудут параллельны.      Поэтому условием параллельности векторовбудет пропорциональность их соответствующих координат:.Пример. Найти длину медианы СЕ в треугольнике АВС с вершинами: А (3,3), В (–1,1), С (0,1).      Решение. Так как Е – середина отрезка АВ, то по формуле (4) имеем:      .      Длину медианыСЕ найдем по формуле (1):      .Пример. Какие из векторов будут параллельны и какие перпендикулярны между собой?      Решение. Векторыперпендикулярны, т.к.. Векторыпараллельны, т.к..Пример. Найти геометрическое место точек, удаленных от точки А(а,b) на одно и тоже расстояние R.      Решение. Если М(х,у) – произвольная точка искомого геометрического места, то всегда |АМ|=R или ,      (х-а)² + (у-b)² = R² – искомое уравнение.

18.Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c - сжатым. В случае, когда a=b=c, эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

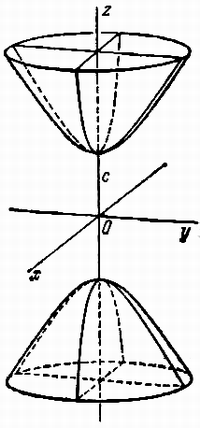
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), - двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), - гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q. Пусть М - произвольная точка пространства, не лежащая на плоскости,- основание перпендикуляра, опущенного на плоскостьиз точки М. Переместим точку М по прямойв новое положениетак, чтобы имело место равенство

и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости; точки, которые расположены на плоскости, оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости, переместятся; при этом расстояние от каждой точки до плоскостиизменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F’. Будем говорить, что поверхность F’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия.

ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть- точка, в которую переходит при этом точка. Выразим координаты x’, y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y. С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число, то.

Таким образом, мы получаем искомые выражения:

,,(6)

или

,,(7)

Предположим, что M(x; y; z) - произвольная точка сферы

.

Заменим здесь x, y, z их выражениями (7); получим

,

откуда

.

Следовательно, точка M’(x’; y’; z’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

,,;

тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

Однополостный гиперболоид

имеет две системы прямолинейных образующих, которые определяются уравнениями:

,;

,,

где и- некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

,;

,.

Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L. Точка S называется вершиной конуса; линия L - направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

20. Свойства пределов.

Обозначение предела Предел функции обозначается как , приили через символ предела.

Всюду ниже предполагается, что пределы функций существуют.

Рассмотрим основные свойства пределов.

1. Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2. Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

3. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4. Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

5. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6. Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

7. Предел степенной функции

где степень p - действительное число.

8. Предел показательной функции

где основание b > 0.

9. Предел логарифмической функции

где основание b > 0.

10. Теорема "о двух милиционерах"

Предположим, что для всехx близких к a, за исключением, быть может, самой точки x = a. Тогда, если

то

То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

 [

Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы ии докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . ТочкаH — проекция точки K на ось OX.

Очевидно, что:

(1)

(где — площадь сектора)

(из :)

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Второй замечательный предел

или

Доказательство второго замечательного предела:

  Докажем вначале теорему для случая последовательности

По формуле бинома Ньютона:

Полагая , получим:

      (1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величинывозрастают. Поэтому последовательность—возрастающая, при этом

     (2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

Поэтому (3).

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3):.

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквойe. Т.е.

  Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами:, где— это целая часть x.

Отсюда следует: , поэтому

.

Если , то. Поэтому, согласно пределу, имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку, тогда

.

Из двух этих случаев вытекает, что для вещественного x.

Следствия

1. 

2. 

3. 

4. 

5. для ,

6. 

21.

Неопределенности типа Пусть заданы две функции f (x) иg (x), такие, что В этом случае говорят, что функция имеет неопределенность типав точкеx = a. Чтобы найти предел при x = aкогда функциясодержит неопределенность, нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используетсяправило Лопиталя. Неопределенности типа Пусть две функции f (x) иg (x) обладают свойством где aявляется действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция имеет в точке aнеопределенность типа. Для вычисления предела в этой точке необходимо разделить числитель и знаменатель наxв наивысшей степени. Неопределенности типа Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа и.

Пример 1

Вычислить предел . Решение. Подставив напрямую значение x = 1, убеждаемся, что данная функция имеет неопределенностьв точкеx = 1. Разложив числитель на множители, получаем

28. Физический смысл производной Предположим, что функция у = f (x) описывает закон движения материальной точки М по прямой линии, т.е. y = f (x) — путь, пройденный точкой М от начала отсчета за время х. Тогда за время х0 пройден путь y = f (x0), а за время х1 — путь y = f(x1). За промежуток времени Δх= х1 - х0 точка М пройдет отрезок пути Δ y = f (x1) - f (x0) = f (х0+ Δх) - f(x0). Отношение называется средней скоростью движения за время Δх, а предел отношения определяет мгновенную скорость точки в момент времени х0. Производная функции в данной точке характеризует скорость изменения функции в данной точке.