
Аналитическая геометрия 4
.pdf
Выберем систему координат следующим образом: ось OX проведем через фокус F перпендикулярно директрисе l. Начало координат О поместим
на равных расстояниях от F и l.
M(x;y) – производная точка гиперболы |
|
|
|
|
|
|
|
|
y |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
F( |
|
|
|
|
) – фокус |
|
N(- |
|
|
) |
|
M(x;y) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
F( |
|
) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
N(- |
|
|
|
|
)-основание перпендикуляра |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
|
|
|
–уравнение директрисы |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|MF|=√ |
|
|
|
|MN|=√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Из определений следует:√ |
|
|
|
|
=√ |
|
|
|
|
– уравнение параболы в |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
выбранной системе координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Преобразуем это уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(1)-каноническое уравнение параболы |
|
|||||||||||||||
II. Исследование формы параболы |
|
||||||||||||||||
1) |
Из (1) |
получим: |
|
|
|
|
|
|
|
|
|
|
(1) |
||||
|
расположена справа от оси OY (в правой полуплоскости) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
+√ |
, |
|
любому х соответствуют два |
значения |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
у +√ |
|
–√ |
, |
значит (1) симметрична относительно оси Оx. |
||||||||||||
3) |
Точка пересечение с Ох (с осью симметрии): у=0 х=0. |
|
|||||||||||||||
|
О(0;0)-вершина |
|
|
|
|
|
|
|
y |
|
|||||||
|
параболы. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4) |
Если х +∞, то |y| |
+∞ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22
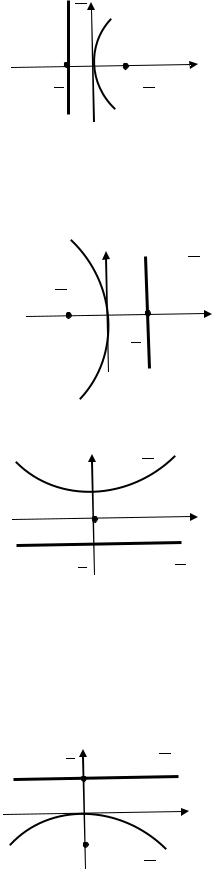
II.Различные виды парабол
1)y2=2px – симметрична относительно Оx,
ветви вправо (в правой полуплоскости)
О(0;0)-вершина
2)y2=–2px – симметрична относительно Ох,
ветви влево (в левой полуплоскости),
О(0;0)-вершина
3)х2=2pу – симметрична относительно
Оу, ветви вверх (в верхней полуплоскости),
О(0;0)-вершина.
4)х2=–2pу – симметрична относительно
Оу,
ветви вниз (в нижней полуплоскости),
О(0;0)-вершина.
y
y2=2px
x
0
y y
0
xx
yy
 x2=2px
x2=2px
|
x |
0 |
x |
y
0
x
23

§6 Преобразование координат
I.Параллельный перенос.
На плоскости введена прямоугольная система координат Oxy. Перенесем точку O в точку и построим новую систему координат , причем
, направления осей совпадают, единицы масштаба
одинаковые.
|
y |
|
|
Y |
|
|
|
|
y |
|
|
|
M |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
X |
X |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
0 |
|
a |
x |
x |
|
|
|
|
|
|
||||
|
Говорят, что выполнен параллельный перенос осей координат, |
||||||
|
причем точка |
имеет координаты |
(a,b) |
в системе Oxy. |
|||
|
M – произвольная точка плоскости. |
|
|||||
|
M(x,y) – в старой системе координат Oxy. |
|
|||||
|
M(X,Y) – в новой системе координат |
. |
|
||||
|
(a,b) – координаты точки |
в старой системе координат. |
|||||
|
Справедливы формулы: |
|
|
|
|||
|
|
|
|
|
|
|
|
|
X=x-a |
|
|
|
|
|
|
|
Y=y-b |
|
- формулы, выражающие новые координаты через старые. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x=X+a |
- формулы, выражающие старые координаты через новые. |
|||||
|
y=Y+b |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Эти формулы называются формулами параллельного переноса. |
||||||
|
Замечание 1. Уравнения вида |
|
|
||||
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
||||
|
определяют параболу с вершиной в точке |
(a,b). |
|||||
|
Действительно, с |
помощью |
формул параллельного переноса |
||||
|
|
|
|
|
|
|
24 |
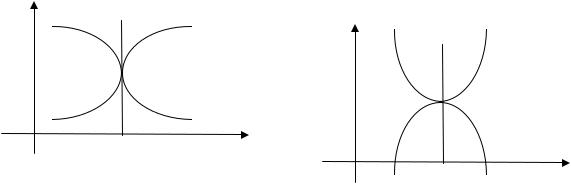
получим: (1) |
=> |
|
(2) |
=> |
– |
параболы с вершиной в новом начале координат .
Осью симметрии параболы (1) является прямая Осью симметрии параболы (2) является прямая
y
|
|
|
y |
|
b |
|
|
|
|
|
O1 |
|||
|
|
|||
|
|
|
b |
|
|
|
|
O1 |
|
|
|
|
|
|
0 |
a |
|
x |
|
a |
x |
Пример 6.1. Найти координаты вершины параболы, построить график
а)
б)
25
Замечание 2.Если в уравнениях эллипса и гиперболы |
заменить X и Y |
|||
соответственно на |
и |
, то полученные |
уравнения |
будут |
определять те же линии, но |
со смещенным центром (вместо |
будет |
||
) |
|
|
|
|
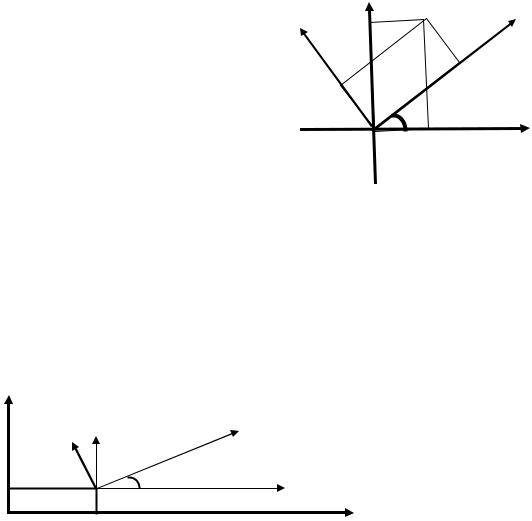
II. Поворот осей координат.
На плоскости задана прямоугольная система координат Oxy. Повернем координатные оси на угол α, не меняя начала координат. Получим новую
систему координат Oxy.
y
М – произвольная точка плоскости |
Y |
y |
M |
X |
|
|
|||
|
|
|
|
|
М(x;y) – в старой системе координат Оху |
|
|
|
X |
|
|
Y |
|
|
M(X;Y) – в новой системе координат OXY
|
α |
|
0 |
x |
x |
|
Тогда |
|
(3) – формулы поворота координатных осей. |
|
|
|
III. Общий случай преобразования координат
Пусть на плоскости заданы две декартовы (прямоугольные) системы координат Oxy и O1XY с разным началом и разными направлениями осей.
y |
y' |
X |
|
||
|
Y |
x' |
|
01 |
α |
b |
|
|
|
|
x
0 a
О1(а,b)-координаты О1 в системе координат Oxy,
α – угол, который образует ось O1Xc осью Ox.
Возьмем т. М
26
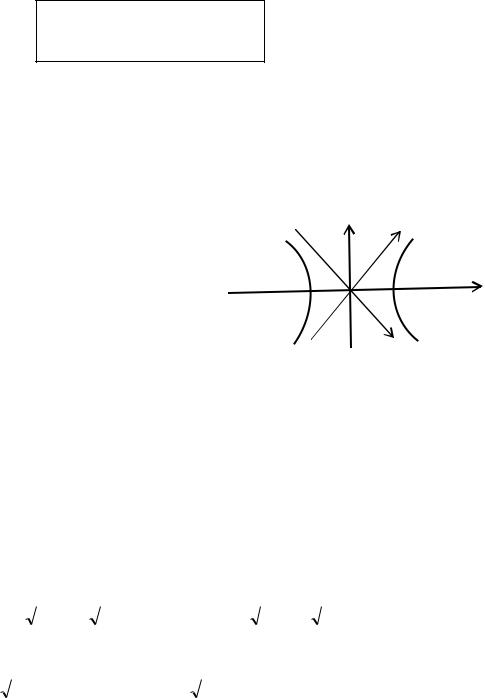
М(x;y) – в координатной плоскости Oxy |
|
|
|
M(X;Y)– в координатной плоскости O1ХУ |
|
|
|
Введем промежуточную систему координат O1 |
, где O1 |
Ox, O1 |
Oy. |
Переход от Oxy к O1XY осуществляется за два шага:
Тогда
α+b
IV. Уравнение равносторонней гиперболы относительно асимптот
x |
2 |
y |
2 |
a |
|
|
|
у=х, у=–х
асимптот.
2 |
– уравнение равносторонней гиперболы. |
|
|
||
|
– уравнения |
|
|
у |
У |
|
0 |
х |
|
|
Х |
Повернем координатные оси на угол
|
|
|
4 |
||
|
. Получим новую систему
координат ОХУ, где новыми осями координат являются асимптоты.
По формулам (3) получим:
x X cos( ) Y sin( |
) , |
|
|
|
|
y X sin( |
) Y cos( |
) |
||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
X |
2 |
|
Y |
|
2 |
|
, |
|
|
|
y |
2 |
|
X |
2 |
|
Y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
2 |
|
|
|
2 |
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
2 |
|
( X Y ) , |
|
|
|
y |
|
2 |
|
( X Y ) |
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
27
Подставим х и у в уравнение равносторонней гиперболы:
( |
|
2 |
( X Y ))2 |
( |
|
2 |
( X Y ))2 |
a2 |
|
|
2 |
|
2 |
||||||
|
|
|
|
|
|
|
|||
1 |
( X 2 2XY Y 2 |
X 2 2XY Y 2 ) a2 |
|||||||
2 |
|||||||||
|
|
|
|
|
|
|
|||
1 |
4XY |
|
2 |
||
|
a |
2 |
|
,
|
a |
2 |
|
XY |
|
||
2 |
|||
|
|||
– уравнение равносторонней гиперболы, когда осями
координат являются асимптоты.
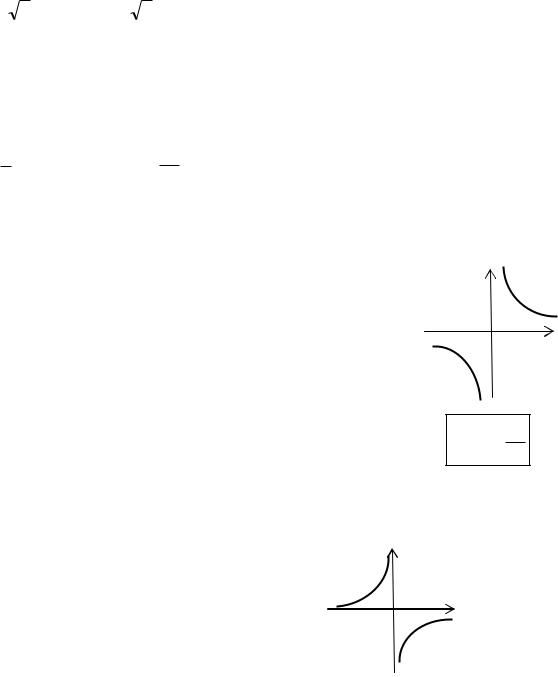
Перерисуем Оху в обычное положение
XУ=k, k>0
Если повернуть оси Ох и Оу на угол |
|
|
, то получим |
|
4 |
||||
|
||||
|
|
|
XУ=k, k<0
У
Х
0
У
0
|
a |
2 |
|
XY |
|
||
2 |
|||
|
|||
Х
.
28
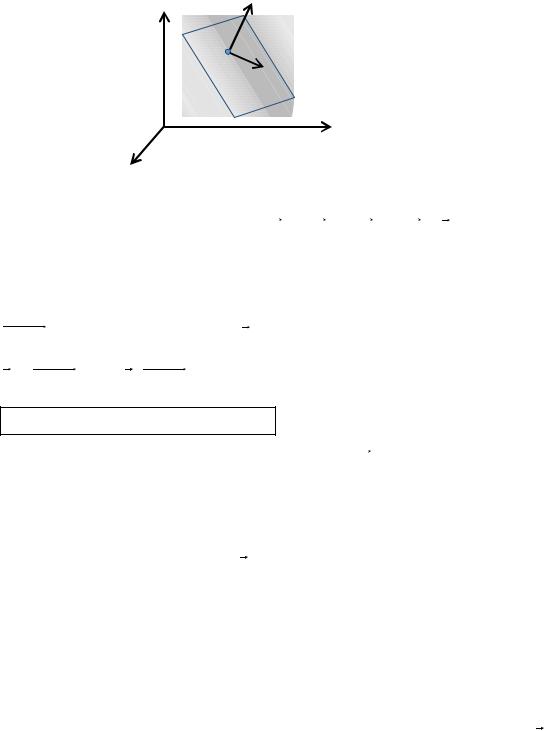
§7. Плоскость в пространстве
I. Уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору. Связка плоскостей.
Пусть Р – произвольная плоскость в пространстве Охуz.
(A;B;C)
z
M0(x0;y0;z0)  M1(x;y;z)
M1(x;y;z)
х |
0 |
у |
|
|
|
|
Дано: т. |
M0 (x0 ; y0 ; z0 ) P , n A i B j C k , |
||||||
|
|
Требуется: составить уравнение плоскости Р. |
|||||||
М(х;у;z) – произвольная точка плоскости Р. |
|||||||||
M |
0 |
M (x x |
; y y |
0 |
; z z |
0 |
) |
, |
n ( A; B;C) |
|
0 |
|
|
|
|
||||
n P
n M |
M |
0 |
|
n M |
M 0 |
0 |
|
A(x x0 ) B( y y0 ) C(z z0 ) 0 (1) – уравнение плоскости, проходящей
через точку |
M |
0 |
(x |
; y |
0 |
; z |
0 |
) |
перпендикулярно |
n ( A; B;C) |
. |
|
0 |
|
|
|
|
Уравнение (1) – это уравнение первой степени относительно x, y, z.
Пример 7.1. Написать уравнение плоскости, проходящей через точку
M 0 (1; 2;3) перпендикулярно n (2;3; 3) .
Если в уравнении (1) считать, что координаты вектора n , то есть
A; B;C , принимают различные значения, то будем получать уравнения
плоскостей, проходящих через точку M 0 .
29
Опр. Совокупность плоскостей, проходящих через данную точку,
называется связкой плоскостей.
Уравнение (1), в котором А, В, С могут принимать любые значения,
является уравнением связки плоскостей.
II. Общее уравнение плоскости
Докажем, что всякое уравнение первой степени относительно текущих координат x, y, z
Ax By Cz D 0 |
(2) |
|
|
|
|
определяет в пространстве плоскость.
В уравнении (2) А, В, С одновременно не равны 0.
Пусть
C
0
,
тогда из (2) следует
A(x 0) B( y 0) C(z ( |
D |
)) 0 |
|
C |
|||
|
|
–
пришли к уравнению вида (1), которое определяет плоскость, проходящую
через точку
M |
|
(0;0; |
D |
) |
|
0 |
C |
||||
|
|
|
|||
|
|
|
|
перпендикулярно
n
( A; B;C)
, что и требовалось
доказать.
Опр. Уравнение
уравнением плоскости,
Ax By n ( A; B;C)
Cz D 0 |
(2) называется общим |
|
|
|
|
– нормальный вектор.
III. Исследование общего уравнения плоскости
Ax
1)
D
By
0
Cz D 0
Ax By Cz
А, В, С одновременно не равны 0
0 – плоскость, проходящая через начало координат.
30

2)
3)
4)
5)
A 0
B 0
C 0
A D
By
Ax
Ax
0
Cz D 0
Cz D 0
By D 0
By Cz 0
– плоскость, параллельная оси Ох (
– плоскость, параллельная оси Оу
– плоскость, параллельная оси Оz
– плоскость, проходящая через Ох
n(0; B;C)
Ox
).
31
