Висновки

В результаті виконання контрольної роботи я навчився створювати модель технічного процесу «Заміна підшипника».

Список використаних літературних джерел

1. Кузнєцов Ю.М., Луців І.В., Дубняк С.А. Теорія технічних систем. – К.: – Тернопіль, 1998. – 310 c.

6 Приклад виконання Самостійної роботИ з модуля 3

Міністерство освіти та науки України

Кіровоградський національний технічний університет

Механіко-технологічний факультет

Самостійна робота №3

З курсу «Теорія технічних систем»

Варіант №0

Виконав: ст.гр. шифр академічної групи

ПІБ студента

Перевірив: вчений ступінь, вчене звання

ПІБ викладача

Кіровоград 2009

ЗМІСТ

	С
Завдання до виконання самостійної роботи № 3 ……….	33
Вибір найкращого варіанту методом розстановки пріоритетів ………………………………………………………………	34
1.1 Складання матриці суміжності ………………………………………...	34
1.1.1. Визначення компонентів матриці суміжності ……………………..	34
1.1.2. Складання матриці суміжності ……………………………………...	34
1.2 Розрахунки по першій та другій ітерації …….......................................	35
1.2.1. Розрахунки по першій ітерації ……………………………………...	36
1.2.2. Розрахунки по другій ітерації ….……………………………………	37
1.3 Вибір кращого варіанту ………………………………………….…….	38
Висновки ……………………………………………………………..…	38
Список використаних літературних джерел …………..…	38

Завдання №0

до виконання САМОСТІЙНОЇ роботи З модуля 3

Рис.3 – Граф результатів турніру.

1. Вибрати найкращий варіант методом розстановки пріоритетів.

1.1. Скласти матрицю суміжності.

1.2. Провести розрахунки по першій та другій ітерації.

1.3. Вибрати кращій варіант.

2. Зробити висновки з виконаної самостійної роботи з модуля 3.

3 .Навести список використаних літературних джерел.

Вибір найкращого варіанту

методом розстановки пріоритетів

1.1 Складання матриці суміжності

1.1.1. Визначення компонентів матриці суміжності.

На основі графу результатів, що зображений на рис.3 завдання до самостійної роботи визначаємо компоненти матриці суміжності [1]:

– аналізуємо вершину графа , та з врахуванням (3.2) записуємо , , , , ;

– аналізуємо вершину графа , та з врахуванням (3.2) записуємо , , , , ;

– аналізуємо вершину графа , та з врахуванням (3.2) записуємо , , , , ;

– аналізуємо вершину графа , та з врахуванням (3.2) записуємо , , , , ;

– аналізуємо вершину графа , та з врахуванням (3.2) записуємо , , , , .

1.1.2 Складання матриці суміжності.

На основі даних отриманих в п.1.1 складаємо матрицю суміжності [1]:

. (1)

1.2 Розрахунки по першій та другій ітерації.

1.2.1 Розрахунки по першій ітерації.

За формулою (3.3) визначаємо ітеровану силу першого порядку для першого гравця [1]:

. (2)

За формулою (3.3) визначаємо ітеровану силу першого порядку для другого гравця [1]:

. (3)

За формулою (3.3) визначаємо ітеровану силу першого порядку для третього гравця [1]:

. (4)

За формулою (3.3) визначаємо ітеровану силу першого порядку для четвертого гравця [1]:

. (5)

За формулою (3.3) визначаємо ітеровану силу першого порядку для п‘ятого гравця [1]:

. (6)

За формулою (2) та (3.8) визначаємо нормовану ітеровану силу першого порядку для першого гравця [1]:

. (7)

За формулою (3) та (3.8) визначаємо нормовану ітеровану силу першого порядку для другого гравця [1]:

. (8)

За формулою (4) та (3.8) визначаємо нормовану ітеровану силу першого порядку для третього гравця [1]:

. (9)

За формулою (5) та (3.8) визначаємо нормовану ітеровану силу першого порядку для четвертого гравця [1]:

. (10)

За формулою (6) та (3.8) визначаємо нормовану ітеровану силу першого порядку для п‘ятого гравця [1]:

. (11)

1.2.2. Розрахунки по другій ітерації.

За формулою (3.5) визначаємо ітеровану силу другого порядку для першого гравця [1]:

(12)

За формулою (3.5) визначаємо ітеровану силу другого порядку для другого гравця [1]:

. (13)

За формулою (3.5) визначаємо ітеровану силу другого порядку для третього гравця [1]:

. (14)

За формулою (3.5) визначаємо ітеровану силу другого порядку для четвертого гравця [1]:

. (15)

За формулою (3.5) визначаємо ітеровану силу другого порядку для п‘ятого гравця [1]:

. (16)

За формулою (12) та (3.8) визначаємо нормовану ітеровану силу другого порядку для першого гравця [1]:

. (17)

За формулою (13) та (3.8) визначаємо нормовану ітеровану силу другого порядку для другого гравця [1]:

. (18)

За формулою (14) та (3.8) визначаємо нормовану ітеровану силу другого порядку для третього гравця [1]:

. (19)

За формулою (15) та (3.8) визначаємо нормовану ітеровану силу другого порядку для четвертого гравця [1]:

. (20)

За формулою (16) та (3.8) визначаємо нормовану ітеровану силу другого порядку для п‘ятого гравця [1]:

. (21)

1.3 Вибір кращого варіанту

Результати розрахунків, отриманих в п.1.1 та п.1.2 зводимо у таблицю і на основі результатів другої ітерації приймаємо краще рішення.

Як видно з табл.3.1 після першої ітерації за значенням ще складно розставити пріоритети. Проте після другої ітерації за значенням однозначно можна розставити пріоритети в проведеному турнірі, а саме:

• гравець посів перше місце;

• гравець – друге місце;

• гравець – п‘яте місце;

• гравець 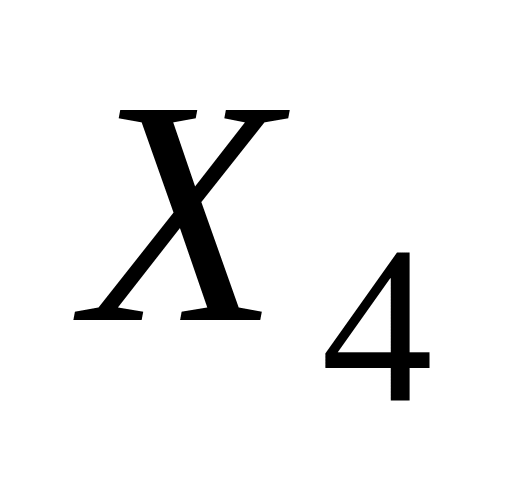– третє місце;

• гравець – четверте місце.

Таблиця 3.1

Результати розрахунків

										Місце
1	2	3	4	5	6	7	8	9	10	11
	1	2	2	1	2	8	0,32	36	0,395	І
	0	1	2	2	2	7	0,28	27	0,297	ІІ
	0	0	1	0	0	1	0,04	1	0,011	V
	1	0	2	1	2	6	0,24	22	0,242	ІІІ
	0	0	2	0	1	3	0,12	5	0,055	ІV
						25	1,00	91	1,00