лекции сапр петраков / 4.Динамический анализ

Лекция 4

Методы решения ММ БИС во временной области.

(динамический анализ)

Задача Коши

Пусть (t) = f(,t) (1)

при условии x(a)=x₀ при .

Основное предположение относительно (1) состоит в том, что удовлетворяет условию Липшеца (в равномерной метрике)

для всех и для всех компонент векторов. При этом можно доказать единственность решения задачи.....

Задача интегрирования с начальными условиями носит название задачи Коши.

Для нахождения (t) численными методами интегрирования разделим интервал времени [a,b] на небольшие приращения. Каждое приращение h_к=t_к называется величиной шага.

Цель численного интегрирования – нахождение (t) для моментов времени

t₁, t₂, t₃ , ... , t_k , где t_i+1 = t_i + h_i (h_i - шаг интегрирования). Численный метод не позволяет найти точное решение, поэтому обозначим вычисленное значение при t=t_k через _k. Равенство _k=|| (t_k) – _k|| называют локальной ошибкой при t=t_k. Локальная ошибка состоит из двух компонент – методической ошибки и ошибки округления в предположение, что значение х на предыдущем шаге известно точно.

Методическую ошибку называют также алгоритмической, поскольку она зависит от вида численного алгоритма.

Как методическая, так и ошибка округления могут накапливаться с увеличением числа шагов. Поэтому для сравнения точности двух алгоритмов необходимо сравнивать их в одни и те же моменты времени t_k при одном и том же начальном состоянии.

Локальная ошибка округления зависит от типа вычислительной машины, т.е. она не может быть уменьшена для данной машины, однако различные методы по разному влияют на ошибку округления. Важно помнить, что общая ошибка округления при t=t_k не равна сумме локальных ошибок округления, возникающих на каждом шаге.

Метод, обладающий свойством уменьшения ошибки округления при увеличении числа шагов, называется численно-устойчивым. В противном случае он численно-неустойчив.

Граница методической ошибки часто обозначается как «О», а сама методическая ошибка как _м= О(h^p) при h  0.

Таким образом, методическая ошибка стремится к 0 с такой же скоростью, как и h^p. Методы классифицируются по критерию «порядок метода p».

В качестве примера рассмотрим линейный многошаговый метод интегрирования, обобщенное выражение которого основано на представлении дифференциальных уравнений разностными уравнениями вида:

(2)

Данное уравнение получено на основе теоремы о среднем.

Теорема о среднем:

₍₃₎

Из общего выражения (2) можно получить формулу явного метода Эйлера (ЯМЭ), задав ₀=0; k=1; ₁=1; ₁=1 .

При этом - ЯМЭ. (4)

Подставив в выражение (2) ₀=1; k=1; ₁=1; ₁=0 получим формулу неявного метода Эйлера (НЯМЭ) (5)

Подставив в выражение (2) ₀=₁=1/2; k=1; ₁=1 получим формулу метода трапеций

(6)

Оценка локальной методической погрешности ЯМЭ и НЯМЭ

Разложим функцию в ряд Тейлора:

где t <  < a при t < a;

a<  < t при a < t.

Определим погрешность

(7)

где первое слагаемое – это точное значение, а второе - приближенное. Будем считать, что на предыдущем шаге решение точное. Отсюда .

Получим формулу локальной методической ошибки для явного метода Эйлера.

Заменив в формуле . заменим на производную (см. формулу (1)), получим

x_n+1 = x_n + h (8)

Поскольку при вычислении локальной методической ошибки значение переменной на предыдущем шаге задается точно, перейдем к следующей формуле

x_n+1 = x(t_n) + h . (9)

Разложим функцию в ряд Тейлора в окрестности точки x_n с точностью до члена второго порядка малости

(10)

где t_n <  < t_n+1

t_n+1 – t_n = h

Сравнивая выражения (9) и (10) с учетом формулы (7) получим локальную методическую ошибку

(11)

Заметим, что локальная методическая ошибка _М довольно велика, поэтому для получения приемлемой точности с помощью явного метода Эйлера необходимо выбирать очень маленькую величину шага.

Аналогично выведем формулу локальной методической ошибки для неявного метода Эйлера.

(12)

Поскольку при вычислении локальной методической ошибки значение переменной на предыдущем шаге задается точным, перейдем к следующей формуле

(13)

Разложим функцию в ряд Тейлора в окрестности точки x_n+1 с точностью до члена второго порядка малости:

(14)

t_n <  < t_n+1

Отсюда:

(15)

Следовательно

(16)

Явный и неявный методы Эйлера можно классифицировать как методы Тэйлора первого порядка. Локальная методическая ошибка определяется второй производной, следовательно, эти методы имеют низкую точность.

Для повышения точности методов необходимо интегрировать с малой величиной шага. Для оценки локальной методической погрешности требуется определить вторую производную.

Вторую производную можно вычислить, используя теорему о среднем (формула (3)).

Вычисление второй производной

Иллюстрируется рисунком 1

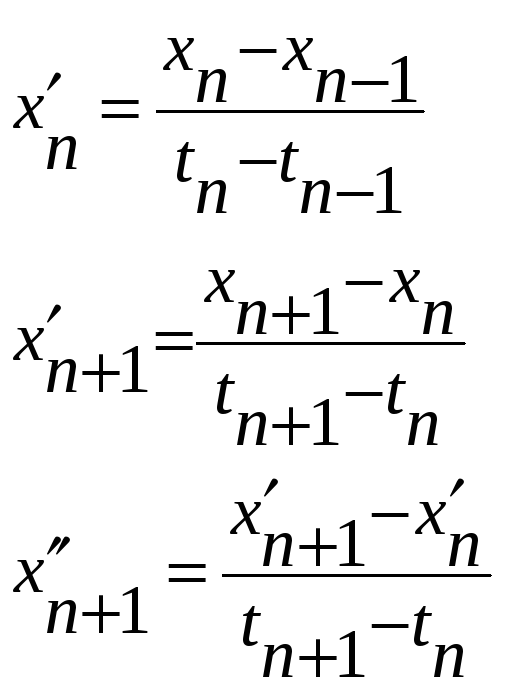
Рис. 1. Иллюстрация вычисления второй производной

Если принять , то выражение для второй производной будет иметь вид:

₍₁₇₎

Подставив формулу (17) в выражения для локальной методической ошибки ЯМЭ и НЯМЭ:

получим следующее выражение:

(18)

Управление величиной шага интегрирования

1. Пусть на n-ом шаге интегрирования величина шага - h_n

2. Определяем вектор локальной методической ошибки Максимальная погрешность

3. Если _max > _{заданное}, то шаг отбрасываем и пытаемся проинтегрировать, уменьшив шаг в два раза

4. Если _max ≤ _{заданное} , то h_n+1 = h_n , если 0.25 _{заданное} ≤ _max ≤ _{заданное} ,

h_n+1 = 2h_n, если _max < 0.25 _{заданное.}