Лекция 2 Методы формирования математической модели схемы

Математическая модель(далее будет использоваться сокращение - ММ) – это совокупность объектов в виде чисел, векторов и связей между ними, которая отражает существенные с точки зрения проектировщика свойства изучаемого объекта (логические, принципиальные, топологические схемы).

На каждом этапе проектирования различают ММ объектов и систем. ММ системы, получаемые непосредственно объединением ММ элементов в общую систему уравнений, называются полными ММ. ММ, более простые по сравнению с полными с точки зрения затрат ресурсов ЭВМ (времени и памяти) при их использовании, называютсямакромоделями.

Основные требования к ММ:

1. адекватность (точность);

2. простота (легкий, эффективный подсчет).

Математической моделью электронной схемы(ММС) для последующего анализа является система уравнений, связывающая токи и напряжения в различных компонентах схемы. ММС получается объединением математических моделей элементов в общую систему уравнений. Результирующую систему получают, применяя методы, развитые в теории электрических цепей (методы формирования моделей).

Все методы формирования ММС основаны на топологических уравнениях и компонентных уравнениях. Топологические уравнения отражают связи между элементами в анализируемой схеме. Это уравнения законов Кирхгофа.

Можно выделить базовые компоненты электрических схем, представляющие собой двухполюсники, а также типовые (библиотечные) компоненты и фрагменты схем. Последние часто представляют в форме эквивалентных схем, состоящих из простых двухполюсных элементов.

Компонентные уравненияописывают электрические свойства компонентов.

Примером компонентных уравнений могут служить уравнения для идеальных резистора, конденсатора и катушки индуктивности (для идеальных линейных двухполюсников):

- нелинейная зависимость, - линейная (закон Ома);

-нелинейная зависимость,- линейная;

-нелинейная зависимость,- линейная.

где R, L, C– сопротивление, емкость и индуктивность;UиI– падение напряжения и ток в компоненте, причем индекс характеризует принадлежность переменной компоненте определенного типа. Сложные компоненты (например, транзисторы, трансформаторы) имеют модели из нескольких уравнений.

Виды источников.

Независимые источники:

1. источник напряжения

2. источник тока

Управляемые источники:

1. источник напряжения, управляемый либо током, либо напряжением -,

.

2. источник тока, управляемый либо током, либо напряжением - ,.

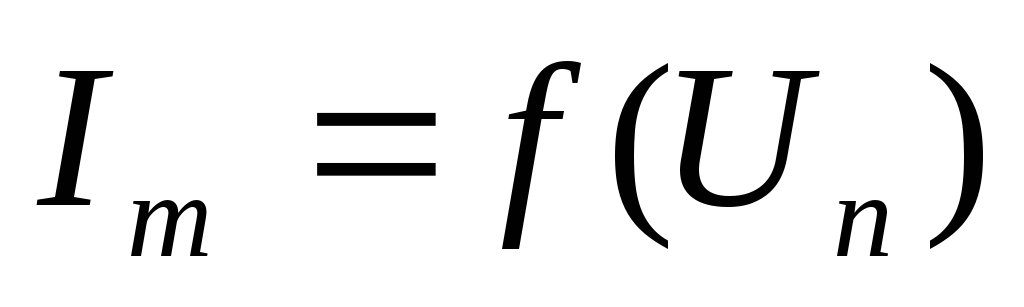Здесь m, n- обозначения управляемых и управляющих ветвей.

Назовем перечисленные элементы базовыми или библиотечными.Эти элементы позволяют реализовать модели более сложных компонентов интегральных схем, таких как транзистор.

Модели МДП и биполярного транзисторов

МДП – транзистор.

Рис.1. Условное обозначение транзистора и простейшая схемная модель

Математическая модель, соответствующая данной схемной может быть представлена формулой

(1)

Биполярный транзистор.

Рис.2. Условное обозначение транзистора и простейшая схемная модель

Математическая модель, соответствующая данной схемной может быть описана следующими соотношениями:

,,, (2)

Для каждого метода формирования ММ характерны свои правила выбора системы исходных топологических уравнений.

Наиболее популярными методами являются метод узловых потенциалов, модифицированный метод узловых потенциалов, табличный метод, метод переменных состояний. Отличия методов заключается в форме получаемых уравнений. Рассмотрим несколько применяемых методов.

1. Метод узловых потенциалов(МУП)

получил широкое распространение в современных программах анализа электронных схем. В вектор базисных координат включаются потенциалы всех узлов схемы, за исключением одного узла, принимаемого за опорный. Исходные топологические уравнения – это уравнения закона токов Кирхгофа, записанные для узлов схемы.

, (3)

где – вектор токов ветвей,– матрица инциденций (матрица «узел-ветвь»). Строки матрицы инциденций соответствуют узлам схемы, а столбцы ветвям.

В столбце i-й ветви записываются единицы на пересечении со строками инцидентных узлов, причем +1 соответствует узлу, а -1 – узлу, из которого этот ток вытекает. Здесь ветвь– ранее перечисленные двухполюсники.Узел – точка, в которой сходится не менее двух ветвей.

Метод предполагает, что независимыми переменными являются потенциалы узлов цепи относительно некоторого базисного опорного узла. МУП допускает следующие элементы:

R, C, L, I(t),.

Исходя из определения метода, можно сделать следующие заключения:

1. ветвь должна иметь конечное сопротивление;

2. источник напряжения не может быть ветвью;

3. ветвью не может быть источник тока, управляемый током (так как ).

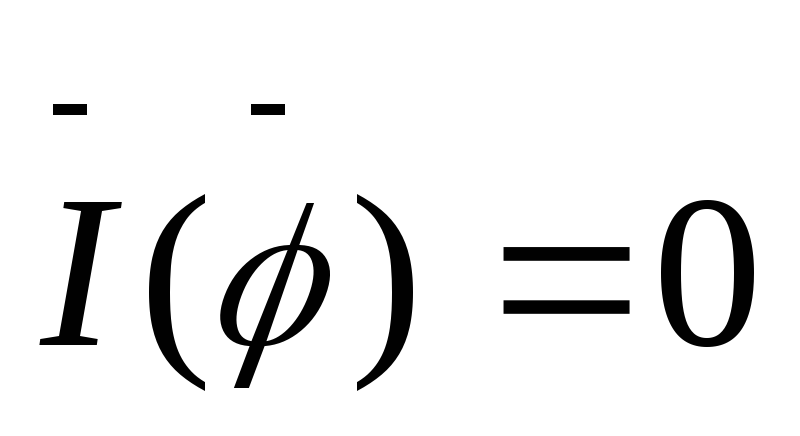Метод приводит к системе обыкновенных дифференциальных уравнений (ОДУ), неразрешенных относительно производных, т.е. к неявной форме ОДУ.

Пример формирования ММС МУП.

Составим математическую модель для принципиальной электрической схемы, представленной на рис. 3.

Рис. 3 Схема принципиальная электрическая

Составим систему уравнений по МУП для узлов 1 и 2:

(4)

Компонентные уравнения имеют вид:

(4),(5),(6),(5)

Подставив компонентные уравнения (4,5,6,7) в систему (3) получим:

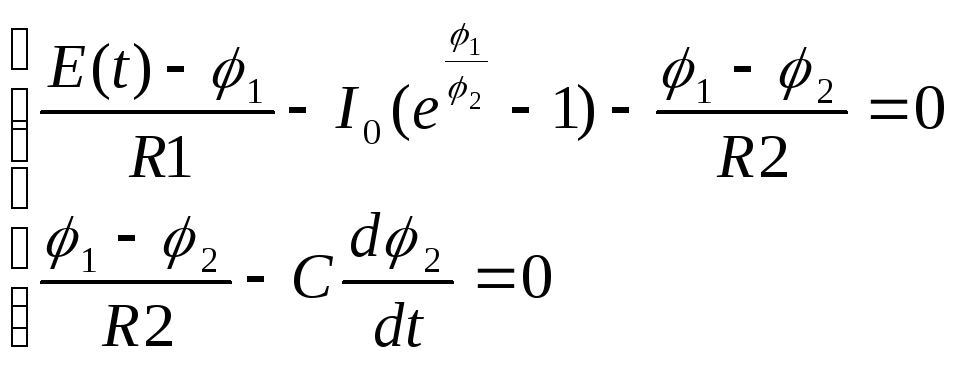(6)