лекции сапр петраков / 5.Анализ многошаговой формулы интегрирования

Лекция 5

Анализ многошаговой формулы интегрирования

Метод простых итераций. Метод ускоренных итераций

Итерации Ньютона-Рафсона. Обратные итерации

При неявных методах интегрирования ОДУ возникают нелинейные алгебраические уравнения. Возвратимся к общему виду линейного многошагового метода. Проанализируем сходимость решения нелинейных алгебраических уравнений.

Требуется решить неявное уравнение:

(1)

т.к. член под знаком суммы известен, то заменим его на w_n, тогда выражение (1) принимает вид:

(2)

Необходимо определить . Рассмотрим некоторые варианты решения.

1. Метод простых итераций (метод Якоби).

Формула метода простых итераций

(3)

Пусть x* - точное решение (2), тогда

(4)

Вычитая, получим

(5)

Используя теорему о среднем, получим:

(6)

где

По условию Липшица тогда

(7)

По индукции

(6)

Принимая во внимание теорему о единственности решения, необходимое и достаточное решение о сходимости итерационного процесса Якоби имеет вид:

(7)

Т.к. L  | _max|, наибольшее собственное значение матрицы -.

Если условие удовлетворено, то итерации Якоби сходятся к единственному решению.

(8)

Для быстрой сходимости необходимо потребовать :

(9)

Границы зависят от h, если | _max | велико, то h должно быть очень мало. Для определения условия окончания итераций рассмотрим случай одного уравнения:

2. Метод ускоренных итераций

Метод ускоренных итераций – модификация метода итераций Якоби

(10)

где параметр ускорения.

Если =0, то получаем простые итерации.

Условие сходимости введем тем же путем.

Точное решение

(11)

Вычитая (11) из (10) и пользуясь теоремой о среднем, получаем:

(12)

Условие сходимости

или , (13)

здесь I – единичная матрица.

3. Итерационный метод Ньютона-Рафсона.

Метод описывается формулой

(14)

где A_n+1^(s) – матрица Якоби f `x, оцененная в точке x(t_n), однократное применение итерации соответствует решению параметризованной формы. Найдем условие сходимости.

Следуя вышеприведенной последовательности действий, получим:

(15)

Применение (14) является неэффективной процедурой: необходимо вычислить на каждой итерации.

4. Обратные итерации.

Рассмотренные выше методы можно отнести к прямым итерациям, т.к. они проходят следующим путем: берем приближение, подставляем в правую часть рекуррентного выражения, затем вычисляем новое приближение и подставляем в правую часть и т.д.

Аналогично можно сформировать уравнения с обратными итерациями в виде:

(16)

которые требуют решения неявных уравнений.

Следуя обычной процедуре, запишем:

Условие сходимости:

или 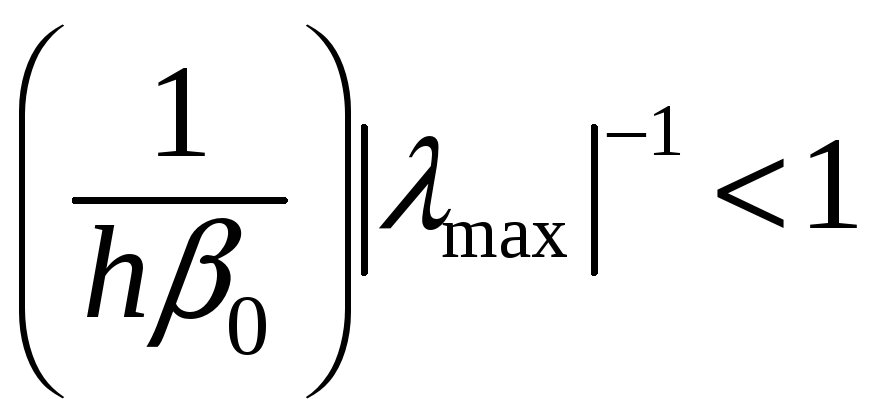– нижняя граница на h.

Краткие выводы:

Итерации Якоби и ускоренные итерации легко реализуются, но сходимость зависит от максимального собственного значения матрицы Якоби. Если |_max | велико, то шаг мал.

Условиям сходимости метода Ньютона посвящено много литературы. Итерации Ньютона имеют большую область сходимости, чем простые и ускоренные. Зато обратные итерации имеют громадную область сходимости из-за наличия нелинейной границы на h, но существует проблема решения неявных уравнений.

Рекомендации:

Если число обусловленности меньше 10, рекомендуется применять простые или ускоренные итерации, иначе использовать итерационный метод Ньютона или методы обратных итераций с выбором шага на основе желаемого числа итераций на шаг. Оптимальное число итераций в корректирующей формуле – 2.

1. Если корректирующая формула в методе не итерируется, то устойчивость метода зависит как от предсказывающих, так и от корректирующих формул.

2. Если корректирующая формула итерируется, то нет уверенности, что устойчивость зависит от корректирующей формулы.