
- •Часть I. Аналитическая геометрия
- •Глава 1. Векторы
- •§1. Сложение векторов и умножение на число
- •§ 2. Коллинеарность и компланарность векторов. Разложение по базису
- •§ 3. Скалярное произведение векторов
- •Задачи для самостоятельного решения
- •§ 4. Операции над векторами в координатах
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Дан правильный шестиугольник
 Точка
Точка – середина стороны
– середина стороны Выразить вектор
Выразить вектор через векторы
через векторы
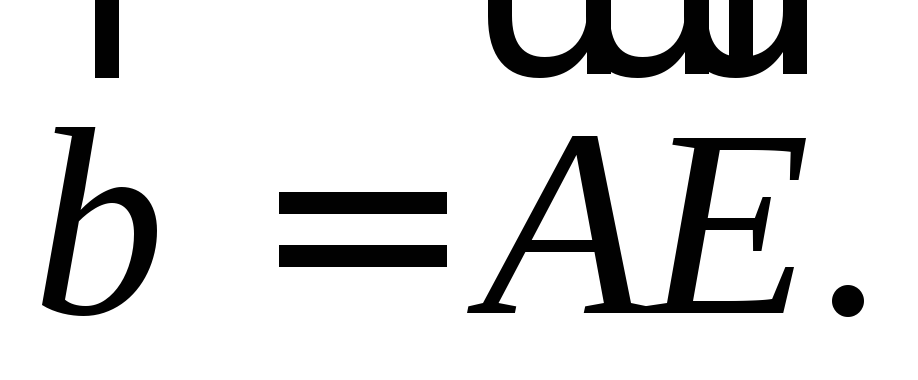
Точка
 – центр правильного шестиугольника
– центр правильного шестиугольника Выразить вектор
Выразить вектор через векторы
через векторы

В треугольнике



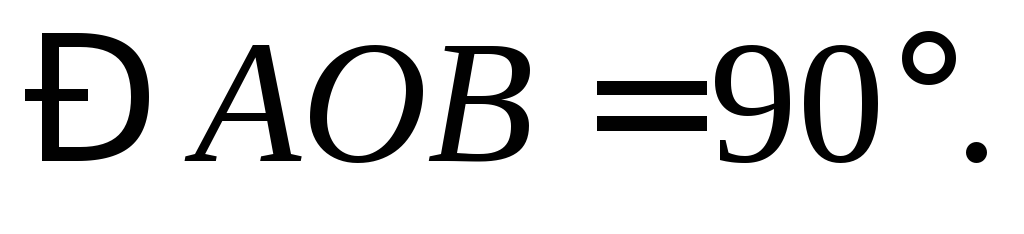 Из точки
Из точки опущена высота
опущена высота Разложить вектор
Разложить вектор по базису
по базису

В треугольнике
 проведены медианы
проведены медианы
 и
и пересекающиеся в точке
пересекающиеся в точке Разложить вектор
Разложить вектор по базису
по базису

В параллелограмме
 точка
точка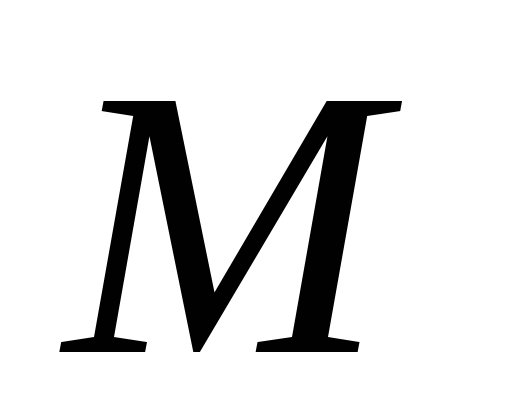 – середина стороны
– середина стороны Разложить вектор
Разложить вектор по базису
по базису

Доказать, что в любой трапеции следующие 4 точки лежат на одной прямой: середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон.
Пусть
 – точка пересечения медиан треугольника
– точка пересечения медиан треугольника а
а – произвольная точка. Доказать, что
– произвольная точка. Доказать, что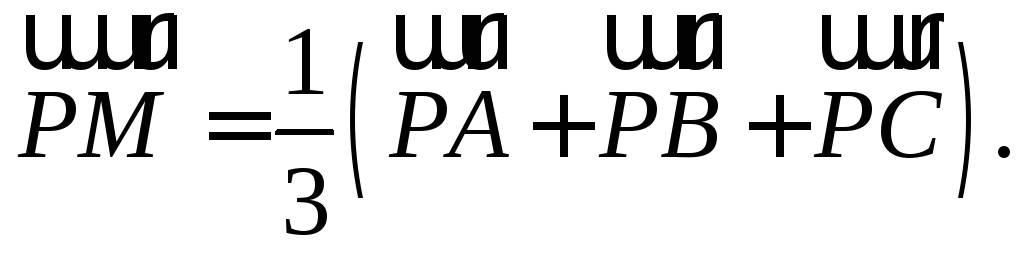
Пусть
 и
и – треугольники,
– треугольники, и
и – точки пересечения медиан этих
треугольников соответственно. Выразить
вектор
– точки пересечения медиан этих
треугольников соответственно. Выразить
вектор через векторы
через векторы и
и
Дан параллелепипед
 Разложить вектор
Разложить вектор по базису
по базису


Ответы:
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() 8.
8.![]() 9.
9.![]()
§ 4. Операции над векторами в координатах
Пусть
дана система координат
![]() на плоскости или
на плоскости или![]() в пространстве. Тогда всякую точку можно
записать в виде
в пространстве. Тогда всякую точку можно
записать в виде![]() (или
(или![]() ),
каждый вектор записывается аналогичным
образом:
),
каждый вектор записывается аналогичным
образом:![]() (или
(или![]() ).
Следует иметь в виду, что запись
).
Следует иметь в виду, что запись![]() эквивалентна записи
эквивалентна записи![]() и аналогично
и аналогично![]() Здесь
Здесь![]() – единичные векторы (орты),
направленные по осям
– единичные векторы (орты),
направленные по осям
![]()
![]()
![]() соответственно.
соответственно.
Операции
над векторами пространства в координатной
форме осуществляются следующим образом:
если
![]()
![]() и
и![]() то
то
![]() (1)
(1)
![]() (2)
(2)
Формула для скалярного произведения выглядит так:
![]() (3)
(3)
Если
![]() и
и![]() – точки пространства, то вектор
– точки пространства, то вектор![]() может быть вычислен по формуле
может быть вычислен по формуле
![]() (4)
(4)
Если
![]() – начало координат,
– начало координат,![]() – произвольная точка пространства, то
– произвольная точка пространства, то
![]() (5)
(5)
Этот
вектор называется радиусом-вектором
точки
![]() Таким образом, радиус-вектор точки имеет
те же координаты, что и сама точка.
Таким образом, радиус-вектор точки имеет
те же координаты, что и сама точка.
Длина
вектора
![]() вычисляется по формуле
вычисляется по формуле
![]() (6)
(6)
а
расстояние
между точками
![]() и
и![]() (т.е. длина вектора
(т.е. длина вектора![]() )
– по формуле
)
– по формуле
![]() (7)
(7)
Формулы, аналогичные формулам (1)-(7), верны также для векторов плоскости.
Замечание. Формулы (1), (2), (4), (5) верны не только в прямоугольной, но также в произвольной косоугольной (или аффинной) системе координат, т.е. такой системы координат, в которой базисные векторы необязательно имеют единичную длину и углы между ними необязательно прямые. Формулы (3), (6), (7) справедливы лишь в прямоугольной системе координат.
Разберём несколько задач на данную тему.
Задача
1. Даны три
вершины параллелограмма
![]()
![]()
![]()
![]() Найти четвёртую вершину
Найти четвёртую вершину![]()
Решение (см. рис. 1).

Рис.1.
Найдём
вектор
![]()
![]() Так как
Так как![]() – параллелограмм, то
– параллелограмм, то![]() Далее поступим следующим образом. Для
того, чтобы найти координаты точки
Далее поступим следующим образом. Для
того, чтобы найти координаты точки![]() достаточно найти координаты её
радиуса-вектора
достаточно найти координаты её
радиуса-вектора![]() где
где![]() – начало координат. Так как
– начало координат. Так как![]() то
то![]() Таким образом,
Таким образом,![]()
Задача
2. Отрезок
![]() разделён точкой
разделён точкой![]() в отношении
в отношении![]() (см. рис. 2). Найти координаты точки
(см. рис. 2). Найти координаты точки![]() считая известными координаты точек
считая известными координаты точек![]() и
и![]()
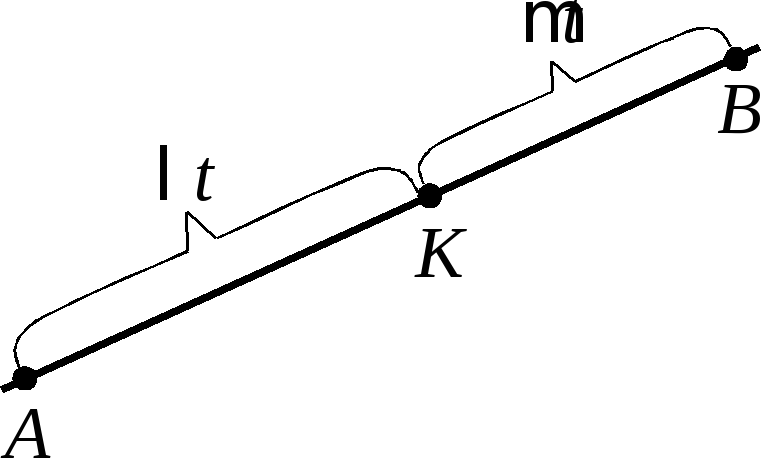
Рис.2.
Решение.
По условию
![]() Пусть
Пусть![]()
![]() Обозначим через
Обозначим через![]() начало координат. Тогда
начало координат. Тогда
![]()
![]()
Таким образом,
![]() (8)
(8)
Замечания. 1. Аналогичная формула
![]()
![]()
справедлива для точек плоскости.
2.
При
![]() мы получаем координаты середины отрезка
мы получаем координаты середины отрезка![]()
![]()
![]()
![]()
Задача
3. Пусть
![]() – точка пересечения медиан треугольника
– точка пересечения медиан треугольника![]() Зная, что
Зная, что![]()
![]()
![]() найти координаты вершины
найти координаты вершины![]()
Решение (см. рис. 3).

Рис.3.
Вычислим
векторы
![]()
![]() и их длины:
и их длины:![]()
![]()
![]()
![]() Мы видим, что
Мы видим, что![]() Следовательно, точка
Следовательно, точка![]() делит отрезок
делит отрезок![]() в отношении
в отношении![]() По формуле
По формуле![]() мы теперь получаем:
мы теперь получаем:![]()
Задача
5. На оси
абсцисс найти точку, равноудалённую от
точек
![]() и
и![]()
Решение.
Пусть
![]() – искомая точка. Тогда
– искомая точка. Тогда![]() при некотором
при некотором![]() По условию
По условию![]() По формуле (7) получаем:
По формуле (7) получаем:![]() Отсюда
Отсюда![]() а значит,
а значит,![]() Таким образом,
Таким образом,![]()
Решим теперь задачи с использованием скалярного произведения векторов.
Задача
6. Найти все
векторы, перпендикулярные вектору
![]() Изобразить эти векторы на чертеже.
Изобразить эти векторы на чертеже.
Решение (см. рис. 5).

Рис.5.
Пусть
![]() Запишем вектор
Запишем вектор![]() в координатном виде:
в координатном виде:![]() Так как векторы
Так как векторы![]() и
и![]() перпендикулярны, то их скалярное
произведение равно нулю:
перпендикулярны, то их скалярное
произведение равно нулю:![]() т.е.
т.е.![]() Получаем:
Получаем:![]()
![]() Очевидно,
Очевидно,![]() – любое действительное число. Значит,
общий вид всех векторов
– любое действительное число. Значит,
общий вид всех векторов![]() таков:
таков:![]() где
где![]() т.е. это в точности те векторы, которые
коллинеарны вектору
т.е. это в точности те векторы, которые
коллинеарны вектору![]() Ровно два из них не только перпендикулярны
вектору
Ровно два из них не только перпендикулярны
вектору![]() но и имеют с ним одну и ту же длину. Это
но и имеют с ним одну и ту же длину. Это![]() и
и![]()
Замечание.
В общем
случае мы имеем: если
![]() то:
то:
![]()
![]()
![]()
![]() (9)
(9)

![]()
![]() или
или
![]() (10)
(10)
Задача
7. Даны две
смежные вершины квадрата:
![]() и
и![]() Найти две другие вершины.
Найти две другие вершины.
Решение.
Обозначим квадрат через
![]() Мы можем считать, что
Мы можем считать, что![]()
![]() Пусть
Пусть![]() – начало координат. Имеем:
– начало координат. Имеем:![]() Вектор
Вектор![]() перпендикулярен вектору
перпендикулярен вектору![]() и имеет с ним одинаковую длину. Поэтому
ввиду утверждения (10) получаем:
и имеет с ним одинаковую длину. Поэтому
ввиду утверждения (10) получаем:![]() или
или![]() (см. рис. 6). Разберём оба этих случая.
(см. рис. 6). Разберём оба этих случая.

Рис.6.
1-й
случай:
![]() Тогда
Тогда![]() т.е.
т.е.![]() Далее,
Далее,![]() т.е.
т.е.![]() Мы получили квадрат
Мы получили квадрат![]()
2-й
случай:
![]() Тогда
Тогда![]()
![]() Таким образом, мы нашли координаты
вершин квадрата
Таким образом, мы нашли координаты
вершин квадрата![]()
![]()
![]()
Задача
8. Найти угол
![]() треугольника
треугольника![]() если
если![]()
![]()
![]()
Решение.
Угол
![]() – это угол между векторами
– это угол между векторами![]() и
и![]() Вычислим эти векторы:
Вычислим эти векторы:![]()
![]() Отсюда
Отсюда

Следовательно,
![]()
