§ 5. Ортогональные операторы. Ортогональные матрицы

Пусть – евклидово пространство. Линейный операторназываетсяортогональным, если он не изменяет скалярного произведения, т.е. для любых

(19)

Из определения следует, что ортогональный оператор не изменяет длин векторов и углов между ними, т.е. сохраняет все геометрические свойства фигур. На плоскости или в трёхмерном пространстве ортогональный оператор определяет движение (например, поворот, симметрию относительно прямой, точки, плоскости).

Матрицу линейного оператора будем обозначать также буквойДля ортогонального оператора имеет место утверждение:

Теорема. Линейный оператор является ортогональным в том и только том случае, если его матрица в ортонормированном базисе удовлетворяет условию

(20)

Условие (20) равносильно условию

Отметим ещё одно свойство ортогональных операторов: собственные значения ортогонального оператора по модулю равны 1. Таким образом, если – собственное значение ортогонального оператора, тодля некоторого

Матрица, удовлетворяющая условию (20), называется ортогональной матрицей. У ортогональной матрицы обратная матрица совпадает с транспонированной. Ортогональную матрицу можно определить и по-другому: ортогональная матрица – это матрица перехода от одного ортонормированного базиса к другому.

Задача 9. Найти общий вид ортогональной матрицы размера

Решение. Пусть – ортогональная матрица. Так както мы имеем:Отсюда получаем систему уравнений:

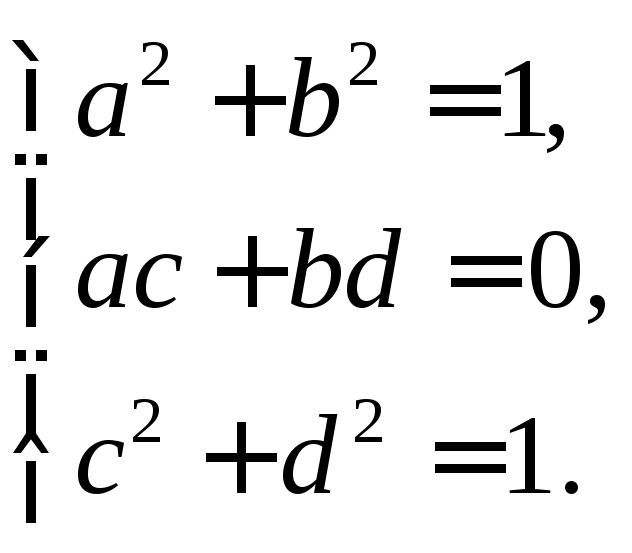
Первое уравнение даёт, что при некоторомИз второго получаем:а значит,при некоторомПодставляя в последнее уравнение системы, получим:т.е.Таким образом, общий вид ортогональной-матрицы таков:

или

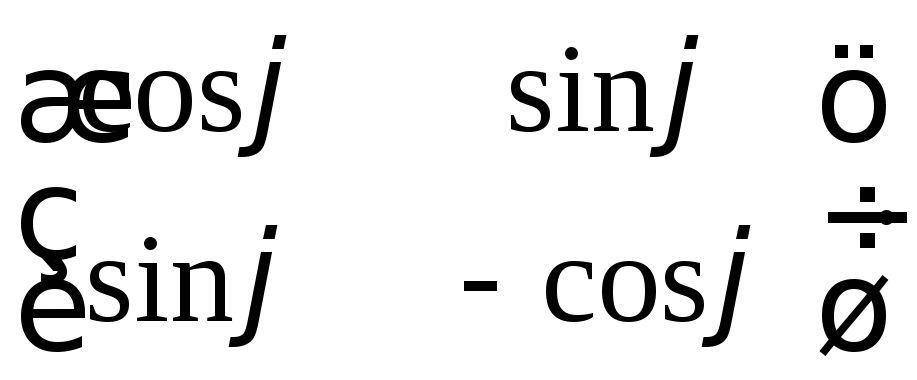
В унитарном пространстве линейный операторсохраняющий скалярное произведение (т.е.), называетсяунитарным. Его матрица в ортонормированном базисе удовлетворяет равенству гдеобозначает, как и раньше, транспонирование, а– матрица, полученная из матрицызаменой каждого элемента на комплексно сопряжённый. Если обозначитьто условие на матрицу будет выглядеть так:Матрица, удовлетворяющая этому условию, называетсяунитарной. Собственные значения унитарного оператора (и унитарной матрицы) по модулю равны 1.

§ 6. Симметрические (самосопряжённые) операторы

Линейный оператор где– евклидово пространство, называетсясимметрическим, или самосопряжённым, если для любых векторов выполняется равенство

(21)

В унитарном пространстве также рассматриваются линейные операторы, удовлетворяющие условию (21), они называются, как и в действительном случае, самосопряжёнными, но слово “симметрический” к ним не применяется.

Необходимые и достаточные условия того, чтобы оператор был симметрическим, даёт следующая теорема.

Теорема. Если линейный оператор является симметрическим, то в любом ортонормированном базисе матрица оператора является симметрической (т.е.). Наоборот, если матрица операторав некотором ортонормированном базисе симметрическая, то операторсимметрический.

Для любого оператора сопряжённый оператор определяется условиемВ каждом ортонормированном базисе его матрица является транспонированной к матрице оператораСимметрический (самосопряжённый) оператор – это оператор, совпадающий с сопряжённым.

Важные свойства симметрических операторов описывает следующая теорема.

Теорема. Пусть – симметрический линейный оператор. Тогда:

1. собственные значения оператора действительны;

2. собственные векторы, соответствующие различным собственным значениям, ортогональны друг другу;

3. пространство имеет ортонормированный базис, состоящий из собственных векторов оператора

Задача 10. Найти ортонормированный базис из собственных векторов линейного оператора, заданного следующей матрицей в ортонормированном базисе:

Решение. Найдём собственные значения и собственные векторы линейного оператора (здесь мы линейный оператор и его матрицу обозначаем одной буквой). Напомним, что собственные значения определяются из характеристического уравнениягде– единичная матрица. Имеем:

Корни характеристического уравнения: Теперь найдём собственные векторы: они находятся из системы линейных уравнений

При имеем:

Найдём фундаментальную систему решений этой системы. Будем считать свободными переменными, а– связанной. Составим таблицу

1	0
0	1	1

Таким образом,

При имеем:

Фундаментальное решение системы:

Мы видим, что вектор перпендикулярен векторам(так и должно быть ввиду сформулированной выше теоремы). Векторыне ортогональны, поэтому к ним следует применить процесс ортогонализации. ПоложимИз условияполучаем:ОтсюдаМы получили ортогональный базис из собственных векторов:Ортонормированный базис из собственных векторов мы получим, разделив каждый из этих векторов на его длину:

В случае унитарного пространства матрица самосопряжённого оператора в ортонормированном базисе удовлетворяет следующему условию:(это комплексный аналог условия симметричностикоторое мы имели в евклидовом пространстве). Матрица, удовлетворяющая этому условию, называетсяэрмитовой. Условие эрмитовости матрицы может быть записано также в видеВ заключение приведём таблицу соответствия понятий в евклидовом и унитарном пространствах.

евклидово пространство		унитарное пространство
симметрическая матрица		эрмитова матрица
симметрический (самосопряжённый) оператор		самосопряжённый оператор
ортогональная матрица		унитарная матрица
ортогональный оператор		унитарный оператор