
Лабы линал / СРС / Глава3
.docГлава 3. Геометрические преобразования
Пусть
дана прямоугольная система координат
![]() на плоскости или
на плоскости или
![]() в пространстве. В теории геометрических
преобразований рассматриваются две
основные задачи, которые мы назовём
задачами А и Б. Сформулируем эти задачи
для случая плоскости, для пространства
они формулируются аналогично.
в пространстве. В теории геометрических
преобразований рассматриваются две
основные задачи, которые мы назовём
задачами А и Б. Сформулируем эти задачи
для случая плоскости, для пространства
они формулируются аналогично.
Задача
А. Пусть
система координат изменилась (например,
претерпела сдвиг или поворот на некоторый
угол) и
![]() – новая система координат. Каждая точка
– новая система координат. Каждая точка
![]() имеет определённые координаты
имеет определённые координаты
![]() в старой (исходной) системе координат
и какие-то координаты
в старой (исходной) системе координат
и какие-то координаты
![]() в новой системе координат
в новой системе координат
![]() Требуется найти связь между новыми и
старыми координатами точки.
Требуется найти связь между новыми и
старыми координатами точки.
Задача
Б. Пусть
система координат
![]() неизменна, а сама плоскость преобразуется,
т.е. точка
неизменна, а сама плоскость преобразуется,
т.е. точка
![]() переходит в точку
переходит в точку
![]() Требуется установить связь между
координатами
Требуется установить связь между
координатами
![]() и
и
![]()
В
каждом случае надо чётко представлять
себе, о какой задаче идёт речь. В задаче
А надо найти связь между координатами
![]() и
и
![]() одной и той
же точки в
разных
системах
координат, а в задаче Б – связь между
координатами
одной и той
же точки в
разных
системах
координат, а в задаче Б – связь между
координатами
![]() произвольной точки и координатами
произвольной точки и координатами
![]() её образа
при данном преобразовании. В обеих
задачах целью является получение формул,
выражающих
её образа
при данном преобразовании. В обеих
задачах целью является получение формул,
выражающих
![]() через
через
![]() а также обратных
формул –
а также обратных
формул –
![]() через
через
![]() Позже средствами линейной алгебры эти
задачи будут разбираться в более общей
ситуации – для п-мерного
пространства.
Позже средствами линейной алгебры эти
задачи будут разбираться в более общей
ситуации – для п-мерного
пространства.
Параллельный
перенос
системы координат
![]() – преобразование, при котором начало
координат переходит в точку
– преобразование, при котором начало
координат переходит в точку
![]() а направления координатных осей
сохраняются. Связь между старыми и
новыми координатами произвольной точки
(решение задачи А) даётся формулами
а направления координатных осей
сохраняются. Связь между старыми и
новыми координатами произвольной точки
(решение задачи А) даётся формулами
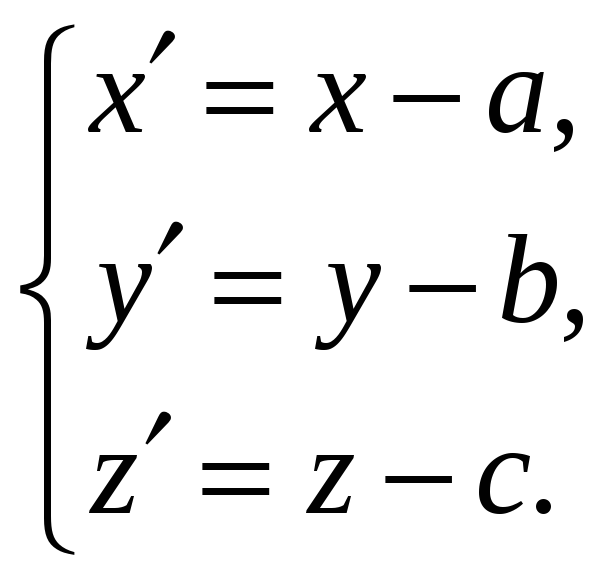 (1)
(1)
Аналогичные формулы справедливы для плоскости (см. рис. 1):
 (2)
(2)

Рис.1.
Поворот
осей
координат
вокруг начала координат на угол
![]() (решение задачи А) даётся формулами:
(решение задачи А) даётся формулами:
 (3)
(3)
(см. рис. 2).

Рис.2.
Обратные
формулы получаются заменой
![]() на
на
![]()
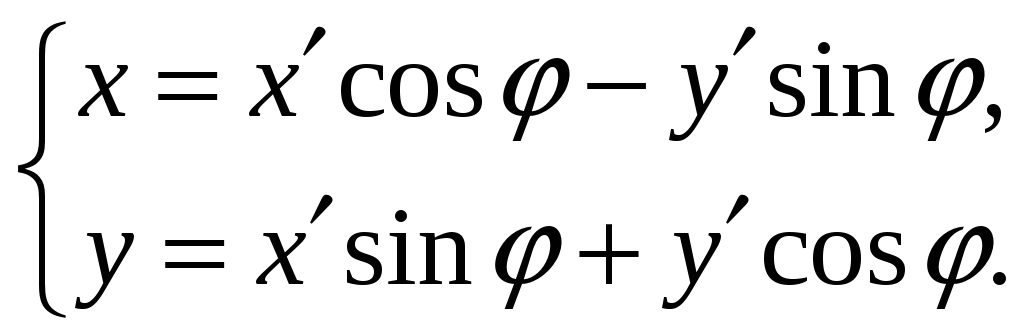
Приведём теперь формулы для задачи Б.
Параллельный
перенос пространства
на вектор
![]() задаётся формулами
задаётся формулами
 (4)
(4)
Параллельный перенос плоскости (см. рис. 3) – формулами
 (5)
(5)
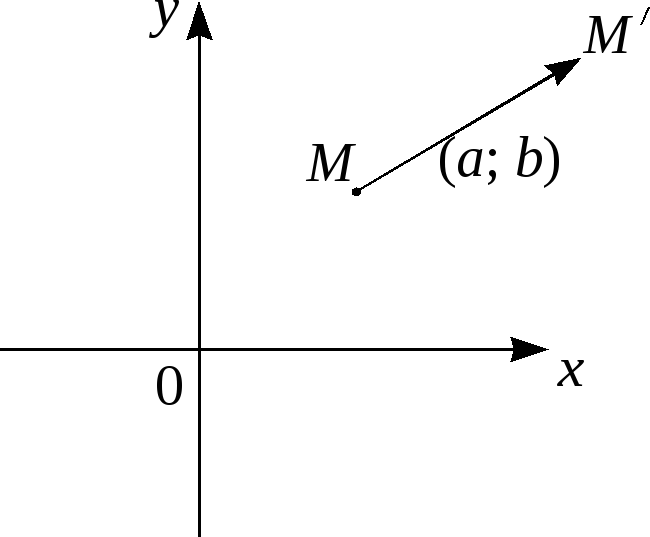
Рис.3.
Поворот
плоскости
на угол
![]() вокруг начала координат
– преобразование плоскости, при котором
каждая точка
вокруг начала координат
– преобразование плоскости, при котором
каждая точка
![]() переходит в такую точку
переходит в такую точку
![]() что угол между векторами
что угол между векторами
![]() и
и
![]() равен
равен
![]() (см. рис. 4).
(см. рис. 4).
Формулы поворота:
 (6)
(6)
Примечание:
здесь речь идёт о направленном
угле, т.е. об
угле от
![]() к
к
![]()
Поворот
плоскости на угол
![]() вокруг точки
вокруг точки
![]()
 (7)
(7)
Симметрии
плоскости (или пространства) – это такие
преобразования плоскости (пространства),
при которых каждая точка
![]() переходит в точку
переходит в точку
![]() симметричную точке
симметричную точке
![]() относительно точки, прямой или плоскости.
Разумеется, это является задачей Б.
Переход от системы координат к симметричной
системе (задача А) встречается весьма
редко и здесь рассматриваться не будет.
относительно точки, прямой или плоскости.
Разумеется, это является задачей Б.
Переход от системы координат к симметричной
системе (задача А) встречается весьма
редко и здесь рассматриваться не будет.
Формулы
симметрии плоскости: а) симметрия
относительно начала координат, б)
относительно оси
![]() в) относительно точки
в) относительно точки
![]() г) относительно прямой
г) относительно прямой
![]()
а)
 б)
б)
 в)
в)
 г)
г)

формулы
симметрии пространства: а) относительно
начала координат, б) относительно оси
![]() в) относительно плоскости
в) относительно плоскости
![]() г) относительно плоскости
г) относительно плоскости
![]()
а)
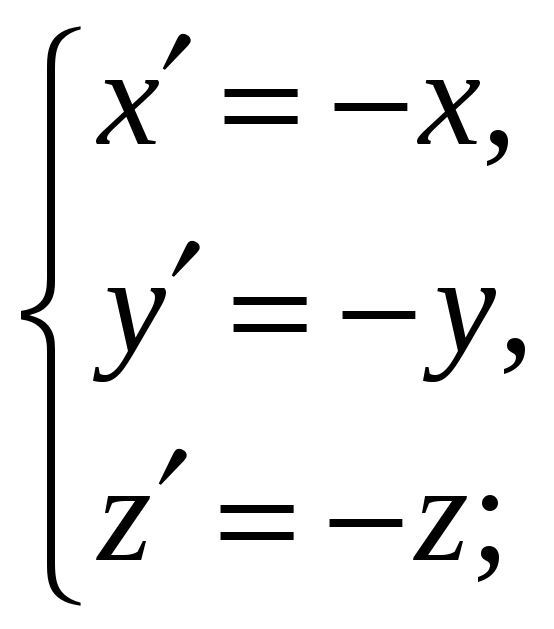 б)
б)
 в)
в)
 г)
г)

Для
симметрий относительно других осей
координат (координатных плоскостей) и
параллельных им прямых (соотв., плоскостей)
формулы пишутся аналогичным образом.
Приведём ещё формулу поворота пространства
на угол
![]() вокруг оси
вокруг оси
![]()

Симметрия
относительно прямой
![]() (или
осевая
симметрия)
– преобразование плоскости, при котором
каждая точка
(или
осевая
симметрия)
– преобразование плоскости, при котором
каждая точка
![]() переходит в точку
переходит в точку
![]() ,
расположенную симметрично
,
расположенную симметрично
![]() относительно
относительно
![]() ,
т.е.
,
т.е.
![]() и
и
![]() лежат по разные стороны от
лежат по разные стороны от
![]() на одинаковом расстоянии от
на одинаковом расстоянии от
![]() на одном перпендикуляре к
на одном перпендикуляре к
![]() .
.
Центральная
симметрия
(симметрия
относительно точки
![]() ):
если
):
если
![]() то
то
![]() Симметрия относительно точки
Симметрия относительно точки
![]() – это поворот плоскости на угол
– это поворот плоскости на угол
![]() вокруг точки
вокруг точки
![]() .
.
Решим две задачи на преобразование координат.
Задача
1. Кривая
задана уравнением
![]() Написать уравнение этой кривой в системе
координат: (а) параллельно перенесённой
на 2 единицы вправо и на 3 единицы вниз;
(б) повёрнутой относительно начала
координат на угол
Написать уравнение этой кривой в системе
координат: (а) параллельно перенесённой
на 2 единицы вправо и на 3 единицы вниз;
(б) повёрнутой относительно начала
координат на угол
![]()
Решение.
(а) Используя формулы (2), получим:
![]()
![]() Напишем обратные формулы:
Напишем обратные формулы:
![]()
![]() Подставим в уравнение кривой:
Подставим в уравнение кривой:
![]() Это и будет уравнением кривой в новой
системе координат.
Это и будет уравнением кривой в новой
системе координат.
Задача
2. Написать
уравнение параболы
![]() в системе координат, повёрнутой на
в системе координат, повёрнутой на
![]() вокруг начала координат.
вокруг начала координат.
Решение.
Взяв в формулах
![]()
![]() получим:
получим:
![]()
![]() Подставим в уравнение
Подставим в уравнение
![]()
 Отсюда получаем, что уравнение параболы
Отсюда получаем, что уравнение параболы
![]() в новой системе координат таково:
в новой системе координат таково:
![]()
Теперь решим несколько задач на преобразование плоскости или пространства.
Задача
3. Кривую
![]() сдвинули на 4 единицы вправо, а затем на
4 единицы вверх. Написать уравнение
новой кривой.
сдвинули на 4 единицы вправо, а затем на
4 единицы вверх. Написать уравнение
новой кривой.
Решение.
По формулам (5) получаем:
![]()
![]() Отсюда получаем:
Отсюда получаем:
![]() или
или
![]() Таким образом, новая кривая имеет
уравнение
Таким образом, новая кривая имеет
уравнение
![]()
Задача
4. Найти образ
точки
![]() при повороте плоскости на угол
при повороте плоскости на угол
![]() вокруг начала координат.
вокруг начала координат.
Решение.
Пусть
![]() – образ точки
– образ точки
![]() Запишем формулы поворота (6) для угла
Запишем формулы поворота (6) для угла
![]()

Подставим
в эти формулы
![]()
![]() Получим:
Получим:
![]()
![]() Следовательно,
Следовательно,
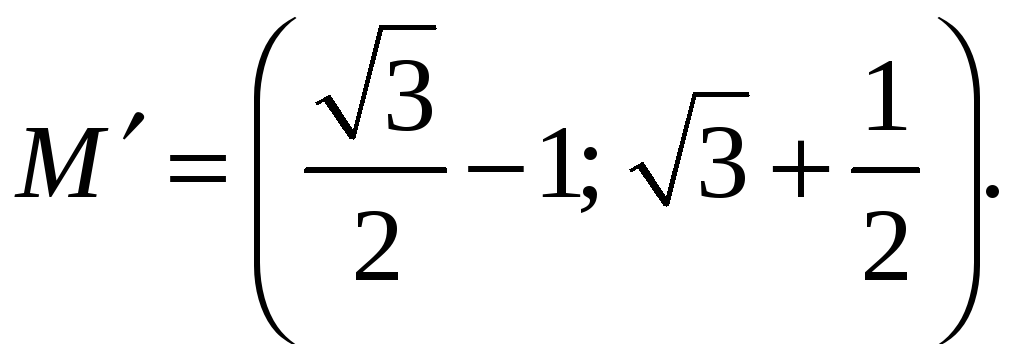
Задача
5. Дана прямая
![]()
![]() Составить уравнение прямой, симметричной
прямой
Составить уравнение прямой, симметричной
прямой
![]() а) относительно начала координат; б)
относительно оси
а) относительно начала координат; б)
относительно оси
![]() в) относительно прямой
в) относительно прямой
![]() г) относительно прямой
г) относительно прямой
![]()
Решение.
Симметрия
относительно начала координат задаётся
формулами
![]()
![]() (формулы (8а)). Подставим в уравнение
прямой
(формулы (8а)). Подставим в уравнение
прямой
![]() вместо
вместо
![]() и
и
![]() вместо
вместо
![]() Получим:
Получим:
![]() Отсюда следует, что
Отсюда следует, что
![]() Значит, уравнение симметричной прямой
таково:
Значит, уравнение симметричной прямой
таково:
![]() б) Применяя формулы (8б), получим:
б) Применяя формулы (8б), получим:
![]() в) Симметрия относительно прямой
в) Симметрия относительно прямой
![]() задаётся формулами
задаётся формулами
![]()
![]() Поэтому следует подставить в уравнение
прямой
Поэтому следует подставить в уравнение
прямой
![]() вместо
вместо
![]() и
и
![]() вместо
вместо
![]() Мы получим:
Мы получим:
![]() Окончательно получаем:
Окончательно получаем:
![]() г) Симметрия относительно прямой
г) Симметрия относительно прямой
![]() определяется формулами
определяется формулами
![]()
![]() Отсюда нетрудно получить уравнение
симметричной прямой:
Отсюда нетрудно получить уравнение
симметричной прямой:
![]()
Задача
6. Найти образ
прямой
![]() а) при повороте плоскости на угол
а) при повороте плоскости на угол
![]() вокруг точки
вокруг точки
![]() б) при симметрии плоскости относительно
точки
б) при симметрии плоскости относительно
точки
![]() в) при симметрии плоскости относительно
прямой
в) при симметрии плоскости относительно
прямой
![]()
Решение.
а) Применяя формулы, обратные формулам
(7), получим:
![]()
![]() Подставим в уравнение прямой:
Подставим в уравнение прямой:

Приводя подобные члены и убирая штрихи, получим окончательно:

б)
Используя формулы (8в), получим:
![]()
![]() Подставим в уравнение прямой:
Подставим в уравнение прямой:
![]() т.е.
т.е.
![]() Убирая штрихи, получим окончательно:
Убирая штрихи, получим окончательно:
![]() в) Заменим
в) Заменим
![]() на
на
![]()
![]() на
на
![]() получим:
получим:
![]() После приведения подобных членов и
удаления штрихов получим:
После приведения подобных членов и
удаления штрихов получим:
![]()
Задача
7. Написать
формулы симметрии плоскости относительно
прямой
![]()
Решение.
Пусть
![]() – произвольная точка плоскости,
– произвольная точка плоскости,
![]() – её образ при симметрии относительно
прямой
– её образ при симметрии относительно
прямой
![]() Тогда
Тогда
![]() Очевидно,
Очевидно,
![]() – направляющий вектор этой прямой.
Точку
– направляющий вектор этой прямой.
Точку
![]() можно найти из следующих условий: 1)
точка с координатами
можно найти из следующих условий: 1)
точка с координатами
![]() (середина отрезка
(середина отрезка
![]() )
принадлежит прямой
)
принадлежит прямой
![]() 2)
2)
![]() Запишем эти условия в виде системы
уравнений:
Запишем эти условия в виде системы
уравнений:

Решив
эту систему, получим:
![]()
![]() Это и есть формулы симметрии.
Это и есть формулы симметрии.
Задача
8. Дан центр
квадрата:
![]() и уравнение
одной его стороны:
и уравнение
одной его стороны:
![]() Составить уравнения других сторон
квадрата.
Составить уравнения других сторон
квадрата.
Решение.
Две стороны (смежные) получаются
поворотом плоскости вокруг точки
![]() на
на
![]() и
и
![]() а
третья сторона (противоположная) –
поворотом на
а
третья сторона (противоположная) –
поворотом на
![]() или, что то же самое, – симметрией
относительно точки
или, что то же самое, – симметрией
относительно точки
![]() Найдём сначала уравнения смежных сторон.
Запишем формулы поворота:
Найдём сначала уравнения смежных сторон.
Запишем формулы поворота:

Отсюда
получаем:
![]()
![]() т.е.
т.е.
 или
или
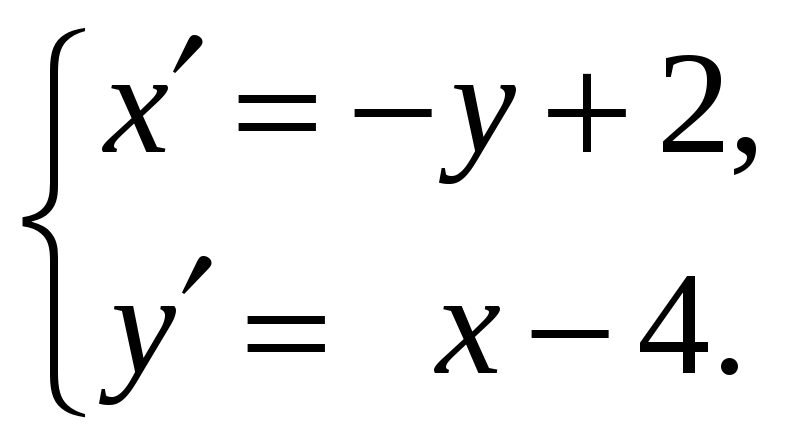
Подставим
оба варианта в уравнение прямой: а)
![]() б)
б)![]() Упростив и удалив штрихи, получим: а)
Упростив и удалив штрихи, получим: а)![]() б)
б)
![]()
Найдём
теперь уравнение противоположной
стороны. Запишем формулы симметрии
плоскости относительно точки
![]()
![]()
![]() Подставим эти формулы в уравнение
прямой:
Подставим эти формулы в уравнение
прямой:
![]() Упростив и удалив штрихи, получим:
Упростив и удалив штрихи, получим:
![]()
Задача
9. Найти образ
точки
![]() при повороте пространства на угол
при повороте пространства на угол
![]() вокруг оси ординат.
вокруг оси ординат.
Решение.
Формулы поворота пространства вокруг
оси
![]() на плоскости
на плоскости
![]() совпадают с формулами поворота этой
плоскости вокруг начала координат, т.е.
мы имеем:
совпадают с формулами поворота этой
плоскости вокруг начала координат, т.е.
мы имеем:
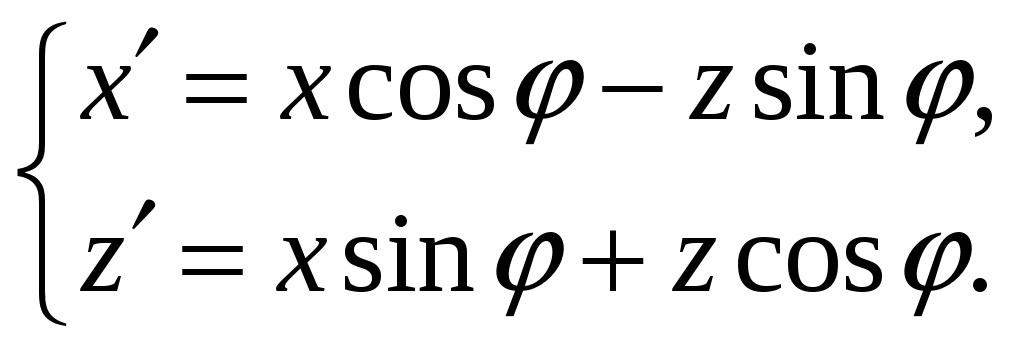
Добавив
уравнение
![]() и подставив
и подставив
![]() получим:
получим:

Взяв
![]()
![]()
![]() вычислим
вычислим
![]()
![]()
![]()
![]() Следовательно, точка
Следовательно, точка
![]() – образ точки
– образ точки
![]() при повороте.
при повороте.
Задача
10. Поверхность
задана уравнением
![]() Составить уравнение поверхности,
симметричной данной относительно
плоскости
Составить уравнение поверхности,
симметричной данной относительно
плоскости
![]()
Решение.
Симметрия относительно плоскости
![]() задаётся формулами
задаётся формулами
![]()
![]()
![]() Подставим в уравнение поверхности:
Подставим в уравнение поверхности:
![]() Убрав штрихи, получим искомое уравнение:
Убрав штрихи, получим искомое уравнение:
![]()
Задачи для самостоятельного решения
-
Точка
 имеет координаты
имеет координаты
 в одной системе координат и
в одной системе координат и
 в другой, получающейся из первоначальной
параллельным переносом. Написать
формулы, выражающие новые координаты
произвольной точки через старые. Ответ:
в другой, получающейся из первоначальной
параллельным переносом. Написать
формулы, выражающие новые координаты
произвольной точки через старые. Ответ:
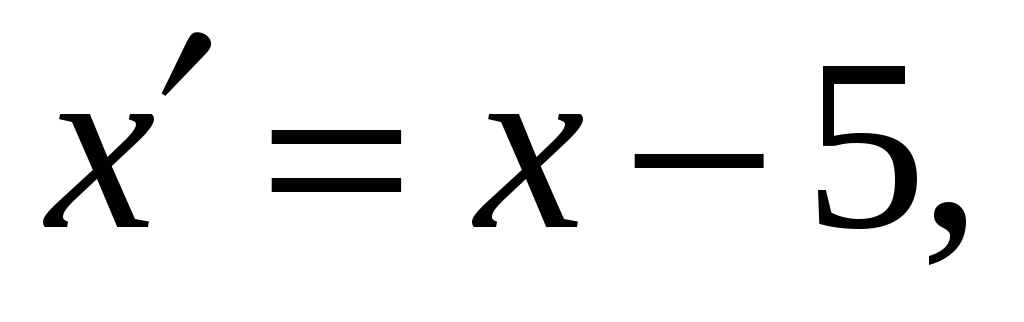
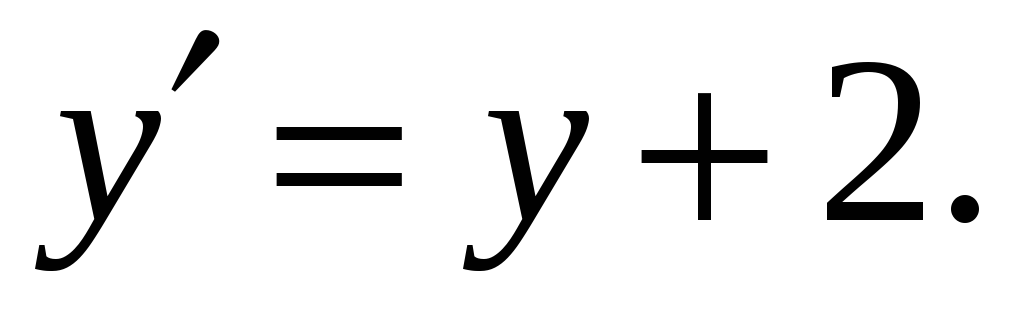
-
Система координат повернулась на угол
 вокруг начала координат. Написать
формулы поворота и уравнение прямой
вокруг начала координат. Написать
формулы поворота и уравнение прямой
 в новой системе координат. Ответ:
в новой системе координат. Ответ:


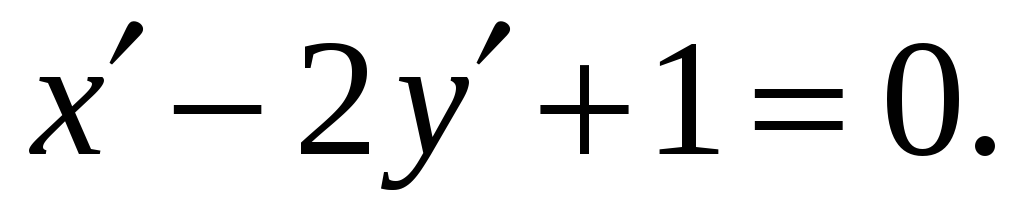
-
Плоскость повернулась на
 вокруг точки
вокруг точки
 Написать формулы поворота. Ответ:
Написать формулы поворота. Ответ:


-
Написать формулы параллельного переноса пространства, при котором точка
 переходит в точку
переходит в точку
 Ответ:
Ответ:



-
Написать уравнение кривой, полученной из кривой
 а) параллельным переносом на 2 вправо
и на 3 вниз; б) симметрией относительно
точки
а) параллельным переносом на 2 вправо
и на 3 вниз; б) симметрией относительно
точки
 в) симметрией относительно прямой
в) симметрией относительно прямой
 г) симметрией относительно прямой
г) симметрией относительно прямой
 Ответ: а)
Ответ: а)
 б)
б)
 в)
в)
 г)
г)

-
Поверхность задана уравнением
 Написать уравнение поверхности,
полученной из данной: а) симметрией
относительно оси
Написать уравнение поверхности,
полученной из данной: а) симметрией
относительно оси
 б)симметрией относительно плоскости
б)симметрией относительно плоскости
 в) симметрией относительно точки
в) симметрией относительно точки
 Ответ: а)
Ответ: а)
 б)
б)
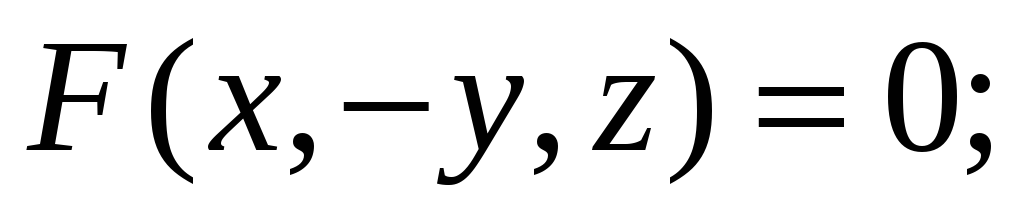 в)
в)
-
Преобразование плоскости задано формулами

 Доказать, что это поворот; найти центр
и угол поворота. Ответ: центр:
Доказать, что это поворот; найти центр
и угол поворота. Ответ: центр:
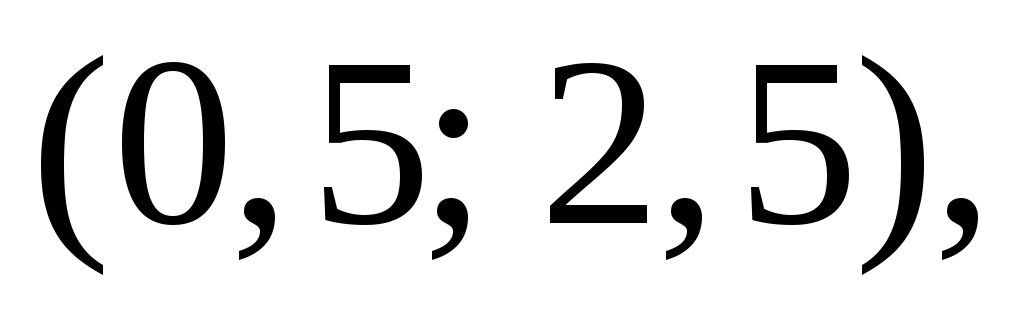 угол:
угол:

-
Дан центр правильного треугольника:
 и уравнение
одной его стороны:
и уравнение
одной его стороны:
 Составить уравнения двух других
сторон. Ответ:
Составить уравнения двух других
сторон. Ответ:

-
Написать формулы симметрии плоскости относительно прямой
 Ответ:
Ответ:


-
Какое преобразование плоскости получится, если сначала сделать поворот на
 вокруг начала координат, а затем на
вокруг начала координат, а затем на
 вокруг точки
вокруг точки
 Ответ: параллельный перенос на вектор
Ответ: параллельный перенос на вектор
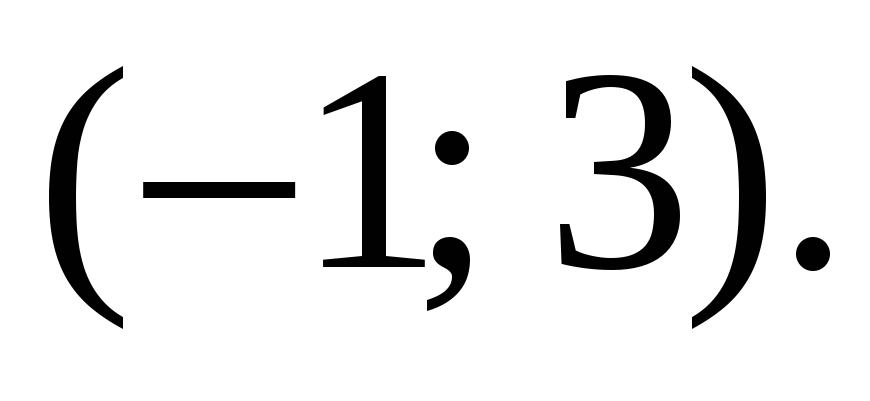
-
