3. Колебательное звено

Колебательным звеном называется звено второго порядка, имеющее передаточную функцию

(1.10)

Дифференциальное уравнение колебательного звена

,

(1.11)

где 0≤ξ<1.

Характеристическое уравнение, соответствующее дифференциальному уравнению ( 1 .11) имеет следующий вид:

корни этого уравнения определяются зависимостью

.

(1.12)

Из выражения ( 1 .12) следует, что при 0 ≤ ξ < 1корни λ₁ и λ₂получаются комплексными, следовательно, для решения уравнения ( 1 .11) будет характерна колебательная составляющая, а приξ ≥ 1корни λ₁ и λ₂–действительные отрицательные и собственное решение уравнения ( 1 .11) будет иметь затухающий апериодический характер.

Определим переходную функцию колебательного звена. Согласно ( 1 .6)имеем:

,

где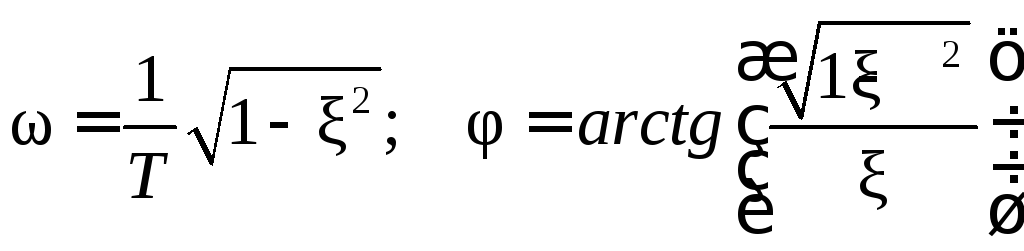

Переходная характеристика колебательного звена показана на Рис.  1 .9.

Рис. 1.9. Переходная характеристика колебательного звена:

Для переходной характеристики колебательного звена параметры Тивычисляют по формулам (Рис.  1 .9.):

;

Рассмотрим случай ξ ≥ 1. Передаточная функция Error: Reference source not found может быть представлена как

,

(1.13)

где ;

В частном случае при ξ = 1, T₁ = T₂.

Звено с передаточной функцией ( 1 .13) (ξ ≥ 1) называется апериодическим звеном второго порядка. Переходная характеристика такого звена имеет вид:

(1.14)

График переходной характеристики ( 1 .14) показан на Рис.  1 .10.

Рис. 1.10. Переходная характеристика апериодическогозвена второго порядка.

Рассмотрим частный случай колебательного звена при ξ = 0.

В этом случае колебательное звено называется консервативным. Его передаточная функция

Переходная характеристика

,

представляет незатухающие гармонические колебания с частотой ω₀(Рис.  1 .11).

Рис. 1.11. Переходная характеристика консервативного звена.

На лабораторном стенде колебательное звено реализовано на R, L, C‑элементах (Рис.  1 .12).

Рис. 1.12. Колебательное звено наR,L,C–элементах.

Передаточную функцию колебательного звена получим из уравнений:

	,

где ;.

Переходный процесс в цепочке R,L,C(Рис.  1 .12) будет колебательным при выполнении условия

,

или

.

2. Работа в системеmAtLab

В проведении эксперимента одной из наиболее удобных прикладных программ для решения задач технических вычислений является система MatLab.

В рамках теории автоматического управления система MatLabпозволяет наиболее быстро и эффективно выполнить математические расчеты при созданиимоделей эксперимента.

1. Рабочее окно программы

Система MatLabимеет графический интерфейс (Рис.  2 .13) – рабочий стол, включающий несколько графических окон: окно текущего каталога, окно просмотра рабочей области, окно предыстории, командное окно.

2. Окно текущего каталога

При работе с файлами в системе MatLabтекущий каталог выполняет роль точки отсчета, например диалоговое окно открытия файла использует в качестве стартового текущий каталог. Любой файл, к которому вы хотите обратиться, должен размещаться либо в текущем каталоге, либо на пути доступа.

3. Окно рабочей области

Окно рабочей области содержит список переменных, накопленных в рабочей памяти системы в процессе сеанса работы. Для каждой переменной указывается размер массива, объем памяти и тип массива. Выводом этой информации можно управлять с помощью опции подменю Workspace View ObjectsменюView.

Рис. 2.13.Графический интерфейс системыMatLab: 1 – окно текущего каталога, 2 – окно просмотра рабочей области, 3 – окно предыстории, 4 – командное окно.

4. Окно предыстории

В окне предыстории фиксируются все команды с параметрами, которые вы вызывали. Это позволяет в конце сеанса работы зафиксировать и сохранить эту последовательность действий, которая привела к решению поставленной задачи, или зафиксировать некоторое промежуточное состояние, т.е. сформировать весь сценарий решения задачи или его часть.

5. Командное окно

Командное окно реализует диалог пользователя с компьютером посредством задания непосредственных инструкций к исполнению. Каждая инструкция после ее ввода сразу исполняется и выдает числовой ответ, либо выполняет некоторое действие – вывод на печать, запись в файл и т.п. Такой режим исполнения инструкций называется режимом интерпретации, и именно он реализован в качестве основного режима.

В режиме командного окна пользователь присваивает значения переменным, исполняет команды и функции, разрешает или подавляет вывод результатов в командное окно.

Следует помнить, что в системе MatLabрегистр имеет значение.