2. Дифференцирующее звено первого порядка

Уравнение идеального дифференцирующего звена первого порядка имеет вид:

.

Практически такое звено реализовать невозможно. Реальное дифференцирующее звено первого порядка описывается уравнением вида:

Передаточную функцию получают из приведенного уравнения

При подстановке р=jимеем следующее аналитическое выражение на АФХ:

Частотная АФХ реального дифференцирующего звена приведена на Рис.  1 .5

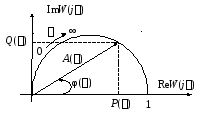
Рис. 1.5. АФХ реального дифференцирующего звена.

Фазо–частотная характеристика дифференцирующего звена имеет положительный знак, т.е. звено создает опережение выходного сигнала относительно входного. Поэтому дифференцирующие звенья называются форсирующими. Выражение для ЛАЧХ имеет вид:

Построение функции второго слагаемого было рассмотрено ранее, а график функции, соответствующий первому слагаемому, представляет собой прямую линию с положительным наклоном 20 дБ/дек и проходит через точку =1/Т. Суммарная ЛАЧХ и фазо–частотная характеристика() для этого звена изображены наРис.  1 .6.

Рис. 1.6. ЛАЧХ и фазо–частотная характеристика реального дифференцирующего звена.

Примером реальных дифференцирующих звеньев могут служить схемы, составленные из R,CиLэлементов (Рис.  1 .7.).

а)		б)

Рис. 1.7. Реальные дифференцирующие звенья наR,CиLэлементах.

Для схемы Рис.  1 .7а:

Обозначая RC=T, можем записать:

Для схемы Рис.  1 .7б:

Обозначив , получим:

или окончательно

3. Колебательное звено

Колебательное звено – это звено второго порядка. Уравнение его имеет вид:

,

причем относительный коэффициент затухания  < 1, и чем он меньше, тем больше колебательность звена.

На основании этого АФХ равна:

Вещественная и мнимая частотные характеристики:

Модуль и фаза частотной характеристики:

На Рис.  1 .8 изображена АФХ колебательного звена для различных .

Рис. 1.8. АФХ колебательного звена.

Выражение для ЛАЧХ звена имеет вид:

.

Асимптотическая ЛАЧХ состоит из двух полупрямых, пересекающихся при . Для ее построения нужно провести прямую вдоль оси частот, соответствующую 20lg(1), до точки=_с(первая асимптота), и из этой точки провести прямую с наклоном в 40дБ/дек (вторая асимптота).

Уравнение асимптотической ЛАЧХ:

т.е. при низких частотах в общем выражении для L() второе слагаемое:

можно считать равным нулю, а при высоких частотах:

.

ЛАЧХ колебательного звена приведена на Рис.  1 .9.

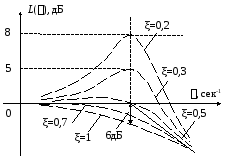
Рис. 1.9. ЛАЧХ колебательного звена.

При малых асимптотическая ЛАХ в точке сопряжения дает большие погрешности и тем больше, чем меньше. Минимальная ошибка при=0,5. Для=1 ошибка в точке_с=1/Тсоставляет 6 дБ. При1 знаменатель передаточной функции можно разложить на два сомножителя первого порядка, т.е. передаточную функцию представить в следующем виде:

.

В этом случае звено называется апериодическим звеном второго порядка.

На Рис.  1 .9 вместе с асимптотической ЛАХ (сплошная линия) приведены и точные характеристики для различных значений (пунктирные линии).

Фазовая характеристика также зависит от , что следует из выражения для

На Рис.  1 .10 представлены несколько () для различных значений.

Рис. 1.10. Фазо–частотная характеристика колебательного звена.

Колебательное звено можно построить на элементах R,CиL(Рис.  1 .11).

Рис. 1.11. Колебательного звено на элементахR,CиL

Связь выходного сигнала звена с входным определяется дифференциальным уравнением второго порядка:

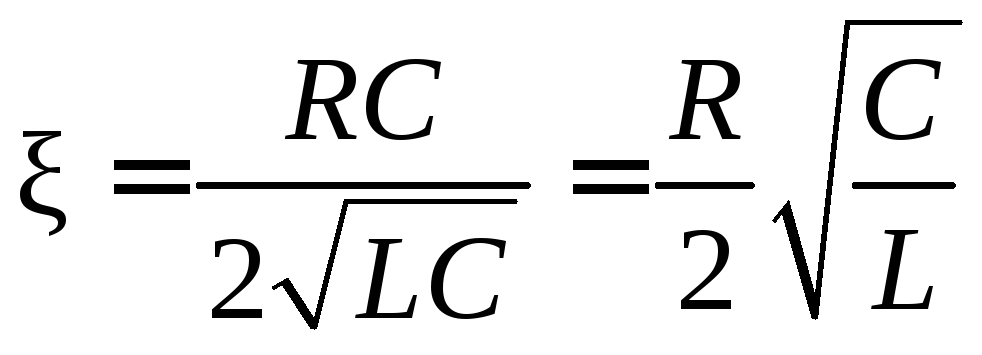Если обозначить и , то передаточная функция на основании вышеприведенного уравнения
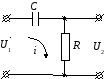
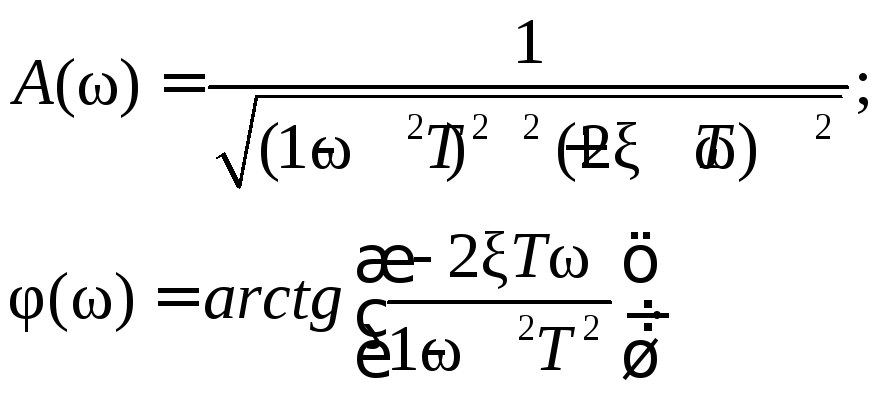
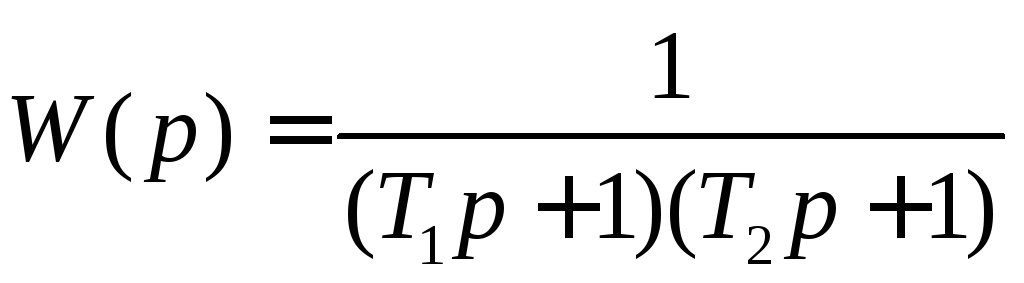