§ 6. Обобщающие примеры по теме: «Системы однородных линейных уравнений»
Набор обобщающих примеров соответствует требованиям «Семестрового плана» при изучении темы: «Системы однородных линейных уравнений». Эти примеры предназначены обеспечить методическими материалами практическую работу студентов в аудитории.
☺ ☻ ☺
Пример
1–724:Найти общее решение
системы уравнений:
и ФСР.
Решение:
1). Применим пошаговый процесс метода Гаусса:
|
1 |
2 |
4 |
-3 |
|
|
1 |
2 |
4 |
-3 |
|
|
3 |
5 |
6 |
-4 |
|
|
0 |
-1 |
-6 |
5 |
|
|
4 |
5 |
-2 |
3 |
=(1)→ |
0 |
1 |
6 |
-5 |
=(2)→ | |
|
3 |
8 |
24 |
-19 |
|
|
0 |
1 |
6 |
-5 |
|
|
1 |
2 |
4 |
-3 |
|
|
1 |
1 |
-2 |
2 |
|
|
0 |
-1 |
-6 |
5 |
|
|
0 |
1 |
6 |
-5 |
|
|
0 |
0 |
0 |
0 |
=(3)→ |
0 |
0 |
0 |
0 |
=(4)→ | |
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
|
Выполнены операции: (1): [R4]–[R2]; делим [R4] на число 3; [R3]–[R2]–[R1]; делим [R3] на (–2); [R2]–[R1]·3. (2): [R4]–[R3]; [R3]+[R2]. (3): [R1]+[R2]; умножим [R2] на число (–1). (4): раскрываем полученный результат.
2).
Видим:
=2.
Свободными неизвестными объявляем
,
.
3). Из уравнения
[R2] следует:
=
;
из уравнения [R1]:
=
,
или
=
. Получено общее
решение: как и в случае неоднородной
системы уравнений.
4). Построим ФСР (свободные неизвестные выделены краснымцветом!):
-
x1
x2
x3
x4
α1
8
-6
1
0
α2
-7
5
0
1
Векторы-решения
,
линейно независимы, их количество
=2.
Эти векторы могут быть приняты в качестве
ФСР.
5).
Используя ФСР, запишем общее решение:
=
+
.
Такая запись общего решения невозможна
для неоднородной системы!
Ответ: общее
решение: x1= –6x3+ 5x4;
x2= 8x3–7x4;
ФСР: 
=
(8, 6, 1, 0); 
=
(–7, 5, 0, 1).
Пример
2–728:Найти общее решение
системы уравнений:
и ФСР.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
6
-2
2
5
7
6
-2
2
5
7
9
-3
4
8
9
3
-1
2
3
2
6
-2
6
7
1
=(1)→
0
0
2
1
-3
=(2)→
3
-1
4
4
-1
0
0
2
1
-3
-
3
-1
0
2
5
3
-1
0
2
5
0
0
2
1
-3
0
0
2
1
-3
0
0
2
1
-3
=(3)→
0
0
0
0
0
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R2]–[R1]; [R3]–[R1]; делим [R3] на число 2; [R4]–[R2]. (2): [R1]–[R2]; [R4]–[R3]; [R2]–[R1];. (3): [R3]–[R2]. (4): раскрываем полученный результат.
2).
Видим:
=2.
Свободными неизвестными объявляем
,
,
.
3). Раскрывая
таблицу, из уравнения [R2]
вычисляем:
=
;
из уравнения [R1]
вычисляем: 
=
. Получено общее
решение: как и в случае неоднородной
системы уравнений.
4). Построим ФСР, избегая дробей в записи решений ФСР:
-
x1
x3
x2
x4
x5
α1
2
0
6
0
0
α2
-4
-3
0
6
0
α3
-10
9
0
0
6
Векторы-решения
,
,
линейно независимы, их количество
=2.
Эти векторы могут быть приняты в качестве
ФСР.
5).
Используя ФСР, запишем общее решение:
=
+
+
.
Такая запись общего решения невозможна
для неоднородной системы!
Ответ: общее
решение:
=
;
=
;
или: 
=
+
+
.
ФСР:
=
(2, 0, 6, 0,0) ; 
=
(–4,–3, 0,6 ,0); 
=
(–10,9, 0, 0,6).
Пример
3–731:Найти общее решение
системы уравнений:
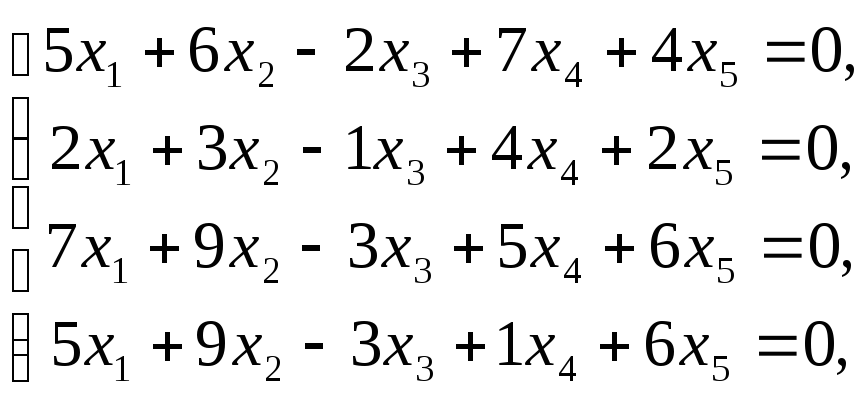и ФСР.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
5
6
-2
7
4
1
0
0
-1
0
2
3
-1
4
2
2
3
-1
4
2
7
9
-3
5
6
=(1)→
2
3
-1
-2
2
=(2)→
5
9
-3
1
6
0
3
-1
-6
2
-
1
0
0
-1
0
1
0
0
0
0
0
3
-1
6
2
0
3
-1
0
2
0
0
0
-6
0
=(3)→
0
0
0
1
0
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R4]–[R1]; [R3]– [R1]; [R1]–[R2]·2. (2): [R3]–[R2]; [R2]–[R1]·2; [R4]–[R2]. (3): [R2]+[R3]; [R3] делим на число (–6); [R1]–[R3]. (4): раскрываем полученный результат.
2).
Видим:
=3.
Свободными неизвестными объявляем
,
.
3). Из уравнения
[R3] следует:
=0;
из уравнения [R2]:
=
;
из уравнения [R1]:
=0. Получено общее
решение: как и в случае неоднородной
системы уравнений.
4). Построим ФСР:
-
x1
x3
x4
x2
x5
α1
0
3
0
1
0
α2
0
2
0
0
1
Векторы-решения
,
линейно независимы, их количество
=2:
Это ФСР.
5).
Используя ФСР, запишем общее решение:
=
+
.
Такая запись общего решения невозможна
для неоднородной системы!
Ответ: общее
решение:
=0,
=0,
=
;
или: 
=
+
.
ФСР:
=
(0,3,0,1,0) ; 
=
(0,2,0,0,1).
Пример
4–735:Найти общее решение
системы:
причем так, чтобы каждое неизвестное
было представлено однородным линейным
выражением от параметров с целыми
коэффициентами.
Решение:
1). Применим пошаговый процесс метода Гаусса:
|
2 |
1 |
-4 |
|
1 |
-3 |
-1 |
|
|
3 |
5 |
-7 |
=(1)→ |
1 |
4 |
-3 |
=(2)→ |
|
4 |
-5 |
-6 |
|
1 |
-10 |
1 |
|
|
1 |
-3 |
-1 |
|
1 |
-3 |
-1 |
|
|
0 |
-7 |
-2 |
=(3)→ |
0 |
1 |
|
=(4)→ |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
Выполнены операции: (1): [R3]–[R2]; [R2]–[R1]; [R1]–[R2]. (2): [R3]–[R2]; [R2]–[R1]; [R3]–[R2]·2. (3): [R2] делим на число (–3). (4): раскрываем полученный результат.
2). Свободной
неизвестной объявляем
.
Примем:
=–7
.
3). Из уравнения
[R2] следует:
=2
;
далее из уравнения [R1]:
=13
.
4). Требование
задания выполнено: при любых целых
значениях параметра
все векторы-решения будут иметь целые
координаты.
Ответ: общее
решение системы:
=13
,
=2
,
=–7
.
Пример
5–738:Найти общее решение
системы:
причем
так, чтобы каждое неизвестное было
представлено однородным линейным
выражением от параметров с целыми
коэффициентами.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
6
-2
3
4
9
3
-1
1
-2
6
3
-1
2
6
3
3
-1
2
6
3
6
-2
5
20
3
=(1)→
0
0
2
16
-6
=(2)→
9
-3
4
2
15
0
0
-2
-16
6
-
3
-1
1
-2
6
1
2
0
0
1
8
-3
0
0
1
8
-3
0
0
0
0
0
=(3)→
0
0
0
0
0
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R4]–[R2]·3; [R3]–[R1]; [R1]–[R2]. (2): [R2]–[R1]; [R4]+[R3]; [R3]–[R2]·2. (3): [R1] делим на число 3. (4): раскрываем полученный результат.
2).
Видим:
=2.
Свободными неизвестными объявляем
,
,
.
Примем значения для свободных неизвестных:
=–3
,
=3
,
=
.
3). Из уравнения
[R2] следует:
=–24
+3
;
далее из уравнения [R1]:
=7
+2
–3
.
4). Требование
задания выполнено: при любых целых
значениях параметров
,
,
все векторы-решения будут иметь целые
координаты.
Ответ:
общее решение системы:
=7
+2
–3
,
=–3
,
=–24
+3
,
=3
,
=
.
Пример
6–741:
Имеем матрицы:
=
,
=
и систему уравнений:
Выяснить, образуют ли строки каждой из
матриц фундаментальную систему решений
заданной системы уравнений.
Решение:
Общая схема решения задачи:
D1: Убедиться, что каждая строка матрицы есть решение.
D2: Проверить, что каждая из матриц имеет ранг равный 3.
D3: Вычислить ранг матрицы коэффициентов системы уравнений: должен быть равен 2.
1). Проверим строки
матрицы
:
являются ли они решениями системы.
Воспользуемся вычислительным шаблоном:
-
30
-24
43
-50
-5
9
-15
8
5
2
4
2
9
-20
-3
3
4
2
1
6
0
3
4
2
1
6
0
3
4
2
1
6
0
5
9
7
4
7
0
5
9
7
4
7
0
5
9
7
4
7
0
4
3
-1
-1
11
0
4
3
-1
-1
11
0
4
3
-1
-1
11
0
1
6
8
5
-4
0
1
6
8
5
-4
0
1
6
8
5
-4
0
Видим:
строки матрицы 
являются
векторами-решениями заданной системы
уравнений.
2). Проверим строки
матрицы
:
являются ли они решениями системы.
Воспользуемся вычислительным шаблоном:
-
4
2
9
-20
-3
1
-11
2
13
4
9
-15
8
5
2
3
4
2
1
6
0
3
4
2
1
6
0
3
4
2
1
6
0
5
9
7
4
7
0
5
9
7
4
7
0
5
9
7
4
7
0
4
3
-1
-1
11
0
4
3
-1
-1
11
0
4
3
-1
-1
11
0
1
6
8
5
-4
0
1
6
8
5
-4
0
1
6
8
5
-4
0
Видим:
строки матрицы 
являются
векторами-решениями заданной системы
уравнений.
3). Использованием
элементарных преобразований вычисляем:
ранг
равен 2, ранг
равен 3. Вывод: строки матрицы
есть совокупность векторов-решений, нозависимая→ не
может служить ФСР для заданной системы;
строки матрицы
есть совокупность векторов-решений,независимая→
может служить ФСР для заданной системы
уравнений, если для неё выполнено условиеD3.
4). Вычислим ранг матрицы коэффициентов системы уравнений, применяя элементарные преобразования:
-
3
4
2
1
6
3
4
2
1
6
5
9
7
4
7
1
6
8
5
-4
4
3
-1
-1
11
=(1)→
1
-1
-3
-2
5
=(2)→
1
6
8
5
-4
0
0
0
0
0
-
1
6
8
5
-4
0
0
0
0
0
1
6
8
5
-4
1
6
8
5
-4
1
-1
-3
-2
5
=(3)→
1
-1
-3
-2
5
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R2]–[R3]; [R4]–[R2]; [R3]–[R1]. (2): [R1]–[R3]·2. (3): [R1]–[R2]. (4): раскрываем полученный результат.
Очевидно: ранг матрицы коэффициентов системы уравнений равен 2.
5). Вывод: строки
матрицы
можно использовать как ФСР для заданной
системы уравнений.
Ответ:
строки матрицы
не могут использоваться в качестве ФСР
заданной системы уравнений, а строки
матрицы
могут.
Пример
7–749:Для системы
уравнений:
найти частное и общее решения, используя
миноры матрицы, составленной из
коэффициентов системы уравнений.
Решение:
1). Построим матрицу:
=
.
Известно, что для систем линейных
однородных уравнений, в которых число
уравнений на 1 меньше числа неизвестных,
можно записать:
▫ частное
решениев виде:
=
,
=–
,
=
,
где
–
соответствующие миноры матрицы
.
▫ общее
решениев виде:x=
·
(
,–
,
),
где параметр
–
произвольное число.
2). Вычислим:
=
=–2,
=
=6,
=
=7
→ частное решение: (–2,–6,7).
3). Запишем общее
решение:
=
·(–2,–6,7).
Ответ:
частное решение: (–2,–6,7); общее
решение:
=
·(–2,–6,7).
Пример 8–776:Найти условие, необходимое и достаточное для того, чтобы четыре точки: (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), (x4, y4, z4), лежали в одной плоскости.
Р
ешение:
1). Так как все3-мерные пространства изоморфны, то
воспользуемся известным в геометрии
утверждением: всякие три точкиM1,M2,M3,
не лежащие на одной прямой, однозначно
определяют плоскость. Для того, чтобы
произвольная точкаMпринадлежала той же плоскости, нужно,
чтобы определяемые этими точками
векторы
=
,
=
,
=
были компланарными. Условие компланарности
этих векторов записывают в виде
определителя (смешанное произведение
векторов):
=(1)=
=(2)=
=(3)=0,
где: (1): отмечает переход в соответствии со свойством определителя разложение по столбцу-1;(2): отмечает переход в соответствии со свойством определителя: определитель не изменяется, если к одной его строке прибавить любую другую;(3): отмечает факт равенства нулю смешанного произведения указанных векторов.
2). Осталось
обозначить: M =
M4, и записать окончательно условие
принадлежности четырёх точек одной
плоскости:
=0. (A)
Ответ: условие имеет вид (A).
☻
Вопросы для самопроверки:
Можно ли, применяя метод Гаусса, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
Можно ли решить систему уравнений методом Гаусса, если все значения свободных членов bi , i = 1, 2, …, n равны нулю?
Можно ли любую систему уравнений записать в виде матричного уравнения AX = B?
Можно ли, применяя правило Крамера, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
Можно ли решить систему уравнений по правилу Крамера, если все значения свободных членов bi, i = 1,2, …, n равны нулю?
Как практически применяется теорема Кронекера-Капелли при решении системы линейных уравнений?
Можно ли провести полное исследование системы уравнений без использования теоремы Кронекера-Капелли?
Может ли ранг расширенной матрицы
быть равным 7, а ранг А-матрицы
8 ? а наоборот? Могут ли ранги матриц А и
равняться нулю? Является ли линейным векторным пространством множество всех решений однородной системы линейных уравнений с обычными операциями сложения и умножения на число?
Какова размерность линейного пространства решений однородной системы 8 линейных уравнений с 12 неизвестными, если ранг матрицы системы равен 4?
Что называется фундаментальной системой решений (ФСР) однородной системы линейных уравнений?
Как построить ФСР однородной системы линейных уравнений?
Сколько ФСР можно построить для заданной однородной системы линейных уравнений?
< * * * * * >