§ 5. Связь решений неоднородной и однородной систем уравнений.

Если мы говорим о связи решений неоднородной и однородной систем линейных уравнений, то только в том случае, когда однородная система уравнений соответствует неоднородной. Это соответствие устанавливается очень просто: нужно в заданной неоднородной системе уравнений (3) заменить нулями все свободные члены: =0,. Полученную таким образом однородную систему уравнений (4) называют приведённой:

(3)= 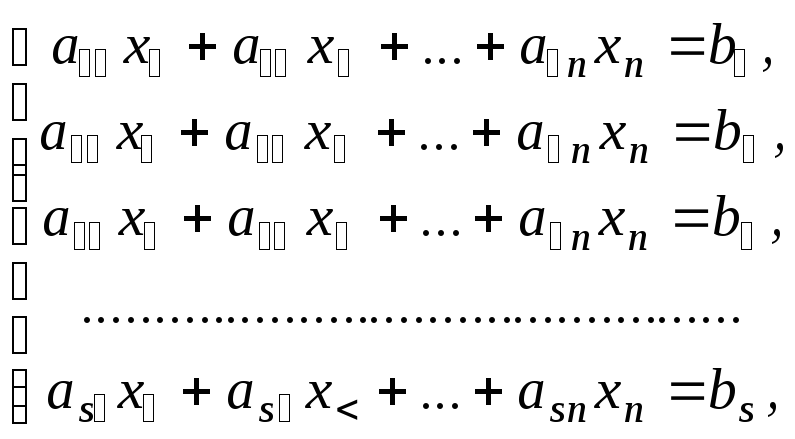→ = (4).

Взаимные свойства заданной и приведённой систем уравнений легко усматриваются:

1). Разность любых двух решений заданной системы уравнений есть решение приведённой системы уравнений.

2). Найдя одно решение системы линейных неоднородных уравнений, и складывая его с каждым из решений приведенной системы, получим все решения заданной системы:

=+++...+, (5)

где – некоторое частное решение заданной системы, ,,..., – векторы-решения ФСР приведенной системы (4), – ранг матрицы системы (3), ,=1,2,..., – произвольные постоянные.

Набор поясняющих Примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений решения линейных однородных систем уравнений.

☺☺

Пример 8–06:Найти общее решение системы уравнений: и ФСР.

Решение:

1). Применим пошаговый процесс метода Гаусса:

3	2	1	3	5			3	2	1	3	5
6	4	3	5	7			0	0	1	-1	-3
9	6	5	7	9	=(1)→		0	0	2	-2	-6	=(2)→
3	2	0	4	8			0	0	-1	1	3

3	2	1	3	5			3	2	2	2	2
0	0	1	-1	-3			0	0	1	-1	-3
0	0	0	0	0	=(3)→		0	0	0	0	0	=(4)→
0	0	0	0	0			0	0	0	0	0

Выполнены операции: (1): [R4]–[R1]; [R2]–[R1]·2; [R3]–[R1]·3. (2): [R3]–[R2]·2; [R4]–[R2]. (3): [R1]–[R2]. (4): раскрываем полученный результат.

2). Видим: =2. Свободными неизвестными объявляем,,.Раскрываемтаблицу:

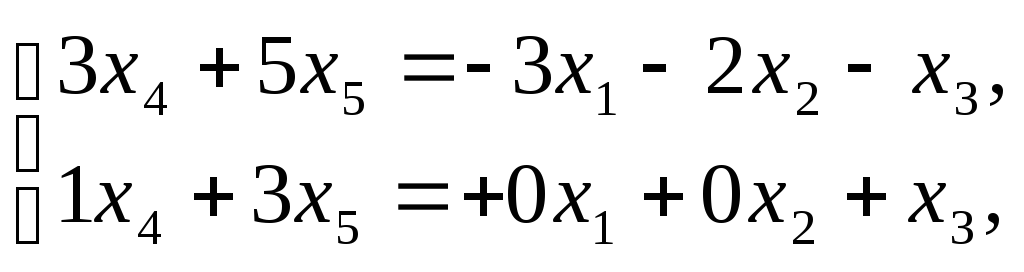
3) Применяем правило Крамера:

= 4;==; ==.

4). Общее решение системы: x₄=; x₅=.

5). Построим ФСР (фундаментальную систему решений), избегая дробей:

	x1	x2	x3	x4	x5
α1	4	0	0	9	-3
α2	0	4	0	6	-2
α3	0	0	4	8	-4

Векторы-решения ,,линейно независимы, их количество=3. Эти векторы могут быть приняты в качестве ФСР.

Ответ: общее решение: x₄=; x₅=;

ФСР: = (4, 0, 0, 9,–3) ; = (0, 4, 0, 6, –2) ; = (0, 0, 4, 8, –4).

Пример 8–07:Найти общее решение системы уравнений: и ФСР.

Решение:

1). Применим пошаговый процесс метода Гаусса:

1	0	-1	0	1	0		1	0	-1	0	1	0
0	1	0	-1	0	1		0	1	0	-1	0	1
1	-1	0	0	1	-1	=(1)→	0	-1	1	0	0	-1	=(2)→
0	1	-1	0	0	1		0	1	-1	0	0	1
1	0	0	-1	1	0		0	0	1	-1	0	0

1	0	-1	0	1	0		1	0	-1	0	1	0
0	1	0	-1	0	1		0	1	0	-1	0	1
0	0	1	-1	0	0	=(3)→	0	0	1	-1	0	0	=(4)→
0	0	-1	1	0	0		0	0	0	0	0	0
0	0	1	-1	0	0		0	0	0	0	0	0

Выполнены операции: (1): [R3]–[R1]; [R5]–[R1]. (2): [R3]+[R2]; [R4]–[R2]. (3): [R4]+[R3] ; [R5]–[R3]. (4): раскрываем полученный результат.

2). Видим: =3. Свободными неизвестными объявляем,,.

3). Из уравнения [R3] следует:=. Далее из уравнения [R2]: =–; из уравнения [R1]: =–. Получено общее решение: как и в случае неоднородной системы уравнений.

5). Построим ФСР (фундаментальную систему решений), избегая дробей:

	x1	x2	x3	x4	x5	x6
α1	1	1	1	1	0	0
α2	-1	0	0	0	1	0
α3	0	-1	0	0	0	1

Векторы-решения ,,линейно независимы, их количество=3. Эти векторы могут быть приняты в качестве ФСР.

Ответ: общее решение =–,=–;=.

ФСР: = (1,1,1,1,0,0); =(-1,0,0,0,1,0); =(0,-1,0,0,0,1).

Пример 8–08:Доказать, что для любой однородной системы линейных уравнений с рациональными (в частности с целыми) коэффициентами можно построить целочисленную фундаментальную систему решений.

Решение:

Для того, чтобы построить целочисленную фундаментальную систему решений, необходимо выполнить действия:

1). Применением пошагового процесса метода Гаусса привести матрицу коэффициентов системы при вычисляемых неизвестных к единичной форме.

2). Вычислим общий знаменатель всех коэффициентов преобразованной матрицы по каждой свободной неизвестной . Обозначим его через.

3). Значения свободной неизвестной будем выбирать так, чтобы в неё входил множитель.

Ответ: алгоритм представлен: хорошо бы применить!

Пример 8–09:Найти общее решение системы: причем так, чтобы каждое неизвестное было представлено однородным линейным выражением от параметров с целыми коэффициентами.

Решение:

1). Применим пошаговый процесс метода Гаусса:

3	2	5	2	7		3	2	5	2	7
6	4	7	4	5		0	0	-3	0	-9
3	2	-1	2	-11	=(1)→	0	0	-6	0	-18	=(2)→
6	4	1	4	-13		0	0	-6	0	-18

3	2	3	2	1		1		1
0	0	1	0	3		0	0	1	0	3
0	0	0	0	0	=(3)→	0	0	0	0	0	=(4)→
0	0	0	0	0		0	0	0	0	0

Выполнены операции: (1): [R4]–[R2]; [R2]–[R1]·2; [R3]–[R1]. (2): [R4]–[R3]; [R3]–[R2]·2; разделим [R2] на число (–3). (3): разделим [R1] на число 3. (4): раскрываем полученный результат.

2). Видим: общий знаменатель всех коэффициентов преобразованной матрицы равен 3. Обозначим его через N.

3). Свободными неизвестными объявляем ,,. Примем:=3,=3,=3.

4). Из уравнения [R2] следует:=–3; далее из уравнения [R1]: =. Подставим значения свободных неизвестных:=–9–2–,=–9.

5). Требование задания выполнено: при любых целых значениях параметров ,,все векторы-решения будут иметь целые координаты.

Ответ: общее решение системы: =–9–2–,=3,=–9,=3,=3.

Пример 8–10:Доказать, что если в однородной системе линейных уравнений число уравнений на единицу меньше числа неизвестных, то в качестве решения можно принять систему миноров, полученных их матрицы коэффициентов поочерёдным вычёркиванием 1-го, 2-го и так далее столбцов, причём миноры берутся с чередующимися знаками.

Решение:

1). Проведём доказательство на примере системы четырёх уравнений с пятью неизвестными. Такой системе соответствует матрицы и:

=→=.

Замечание: в матрице нижняя строка для удобства ссылок на столбцы матрицы, матрица отражает объявление свободной неизвестной и перенос её в правую часть системы.

2). Обозначим определитель левой части преобразованной системы через . Минор матрицыдля элементаобозначим, =1,2,...,5. Применим формулы Крамера:

X1*: Для вычисленияимеем:=, где:=, а для вычисленияв матрицезаменяем столбец-1 на столбец свободной неизвестной; учитывая, что для получения минорапотребуется (5-2)-транспозиций столбцов, учитываем это в записи определителя множителем:=–··=··; учитывая, что=, примем=·; тогда:=.

X2*: Для вычисленияимеем:=; для вычисленияв матрицезаменяем столбец-2 на столбец свободной неизвестной; учитывая, что для получения минорапотребуется (5-3)-транспозиций столбцов, запишем:=–··=··; учитывая, что=·, получим:=–.

X3*: Аналогично получим:=;=–.

Замечание: в записи: =· множитель обеспечивает при любом для первой неизвестной: =, далее используется чередование знаков.

Ответ: доказательство получено: хорошо бы применить!

Пример 8–11:Используя результаты предыдущего примера, найти общее и частное решения для системы линейных однородных уравнений:

Решение:

1). Составим матрицы (для записи миноров) и(для наглядности):

=→=.

2). Вычислим миноры матрицыдля элементов,=1,2,...,4:

==–6,==11,==–9,==4,

3). Частное решение: ==–6,==11,==–9,==4. Общее решение:=–6,=11,=–9,=4.

Замечание: общее решение записано с учётом доказательства, приведённого в предыдущем примере.

Ответ: Частное решение: ==–6,==11,==–9,==4. Общее решение:=–6,=11,=–9,=4.

Пример 8–12:Найти условия, необходимые и достаточные для того, чтобы либо сумма двух решений системы линейных уравнений, либо произведение одного решения этой системы на число, не равное единице, было вновь решением этой системы.

Решение:

Из доказательства теоремы о фундаментальной системе решений следует: система линейных уравнений должна быть однородной!

Ответ: доказано.

Пример 8–13:Решить систему уравнений: записав общее решение в виде суммы частного решения неоднородного уравнения и общего решения присоединённой однородной системы.

Решение:

1). Полное исследование системы позволяют провести как метод Гаусса, так и алгоритм в соответствии с теоремой Кронекера-Капелли. Применим пошаговый процесс метода Гаусса:

12	14	-15	23	27	5			2	2	1	3	4	1
16	18	-22	29	37	8			0	2	-30	5	5	0
18	20	-21	32	41	9	=(1)→		2	2	1	3	4	1	=(2)→
10	12	-16	20	23	4			0	2	-21	5	3	-1

2	2	1	3	4	1
0	2	-30	5	5	0
0	0	0	0	0	0	=(3)→
0	0	9	0	-2	-1

Выполнены операции: (1): [R1]–[R4]; [R3]–[R2]; [R2]–[R1]·8; [R4]–[R1]·5. (2): [R3]–[R1]; [R4]–[R2]. (3): обрабатываем результаты.

2). Получены результаты: - система совместна;

- ранг системы равен 3; свободные неизвестные: и:

- раскрываем строки преобразованной системы:

из уравнения [R4]: =; из уравнения[R2], с учётом найденного значения неизвестной запишем =; из уравнения[R1], с учётом найденных значения неизвестных и : =.

3). Частное решение системы найдём при условии, что свободным неизвестным присвоили значения =1,=1=; =; =, обозначим его: =.

4). Общее решение присоединённой однородной системы: =, =; =. Построим ФСР (фундаментальную систему решений):

	x1	x2	x3	x4	x5
α1	2	-5	0	2	0
α2	-53	15	4	0	18

Векторы-решения , линейно независимы, их количество=2. Эти векторы могут быть приняты в качестве ФСР.

5). Общее решение системы: =+=++.

Ответ: общее решение: =++.

Пример 8–14:Найти условия, необходимые и достаточные для того, чтобы четыре плоскости:

проходили через одну точку.

Решение:

P1*: Чтобы воспользоваться геометрическими образами, полученными при изучении определителей 3-го порядка, сначала рассмотрим только первые три уравнения:

(1)

В геометрии каждому линейному уравнению системы соответствует плоскость. Найти решение системы, значит найти точки, принадлежащие одновременно всем трем плоскостям: α₁, α₂, α₃. Известно, что каждой плоскости соответствует вектор нормали. В нашем случае: , и – строки коэффициентов уравнений и опре­де­ли­теля d. Используя определение смешанного произведения векторов , нетрудно заметить, что == d ≠0 равносильно утверждению, что векторы ,, – некомпланарные → единственность точки, общей трём плоскостям, в этом случае очевидна! Но, эта точка и есть решение системы уравнений.

Если = d =0, то векторы ,, – компланарны! Каким будет взаимное расположение плоскостей α₁, α₂, α₃ в этом случае, и как представится соответствующее ему решение системы – наиболее трудоёмкая часть исследований!

Пустьd ≠0. В этом случае решение системы (21) может быть записано при помощи формул Крамера (используются выражения (23)):

, , .

Полученные формулы определяют единственное решение (т.к. отношение двух чисел, принадлежащих полю вещественных чисел, определяет единственное число!).

Из этого следует, что все заданные плоскости будут пересекаться в одной точке, если каждые из трёх плоскостей будут пересекаться в одной точке. Алгебраические требования в этом случае используют теорему Кронекера-Капелли. А именно, система уравнений:

(2)

должна иметь единственное решение, то есть ранги матриц идолжны быть равны!

Так как решение системы уравнений всегда включает только конечные числа, то проведённый анализ должен сослаться на то, точка пересечения плоскостей конечная!

Если допустить к рассмотрению и бесконечно удалённые точки, то исследования необходимо продолжить.

Вновь обратимся к первым трём плоскостям, то есть к системе уравнений (1). Воспользуемся геометрическими свойствами плоскостей.

2*. Пустьd =0. В этом случае определить координаты точки пересечения плоскостей (x₁, x₂ , x₃), используя формулы Крамера: , , , не удаётся: деление на нуль не определено в поле вещественных чисел. Чем может закончиться решение системы уравнений в этом случае?

1) ,и– компланарны, но плоскости α₁, α₂, α₃ раз­личны: линии их пересечения параллельны → общей точки 3-х плоскостей нет. Следует: система несовместна.

Для исследования соответствия геометрического образа и системы коэффициентов матрицы рассмотрим 4-мерные векторы:

,

,

.

В этом случае ,, – линейно независимы, и поэтому имеем: определители d₁ ≠0, d₂ ≠0, d₃ ≠0.

2) ,и– компланарны, но плоскости α₁, α₂, α₃ раз­личны: линии их пересе­чения совпадают (пучок плоскостей!); общие точки трех плоскостей: общая ли­ния пересечения. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

Для исследования соответствия геометрического образа и системы коэффициентов матрицы воспользуемся 4-мерными векторами: ,

,

.

В этом случае векторы ,, – линейно зависимы, причём так, что один из них является линейной комбинацией двух других: это следует из уравнения пучка плоскостей! Учитывая свойства определителя, имеем: =0, =0, =0. Это значит, что фактически система состоит из двух уравнений, и одной из переменных можно присваивать произвольные значения!

3) ||, но плоскости α₁,α₂,α₃ раз­личны: плоскость α₃ пересекает параллельные плоскости α₁,α₂ по двум параллельным прямым. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: ,

,

линейно независимы! Учитывая свойства определителя, получим: d₁ ≠0, d₂ ≠0, d₃ ≠0.

4) || и плоскости α₁,α₂ совпа­дают: линия пересечения плоско­сти α₃ с плоскостями α₁,α₂ есть об­щие точки всех 3-х плоскостей. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

В соответствии с геометрическим образом, представленном на рисунке, векторы:

, ,

линейно зависимы! Учитывая свойства определителя: d₁ =0, d₂ =0, d₃ =0.

5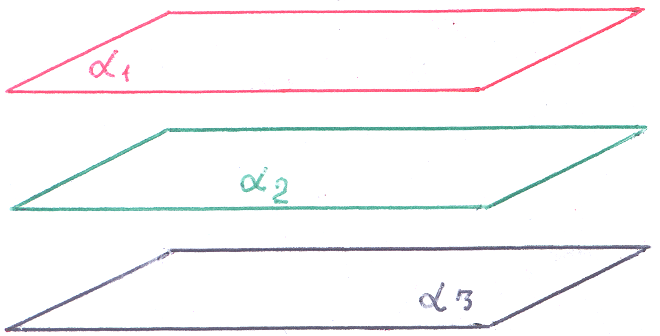) ||||, но плоскости α₁,α₂,α₃ различны (и параллельны): плос­кости α₁,α₂,α₃ не имеют общих то­чек. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы:

, ,

линейно независимы! Учитывая свойства определителя, получим: d₁ ≠0, d₂ ≠0, d₃ ≠0.

6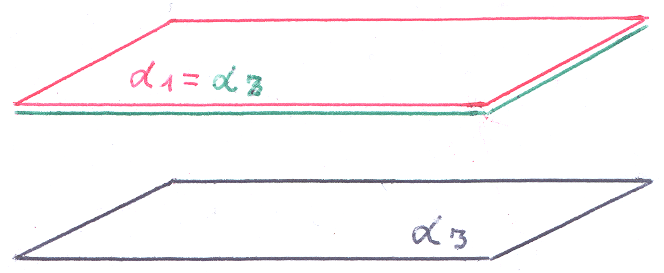) ||||, плоскости α₁,α₂ совпа­дают, плоскость α₃ им параллельна: плоскости α₁, α₂, α₃ не имеют об­щих точек. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: , ,

линейно независимы! Учитывая свойства определителя, получим: d₁ ≠0, d₂ ≠0, d₃ ≠0.

7) ||||, и плоскости α₁,α₂,α₃ совпадают: все точки одной из плоскостей α₁, α₂, α₃ принадлежат двум другим. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: , ,

коллинеарны! Это значит: фактически имеем одно уравнение с тремя неизвестными, и двум из переменных можно присваивать произвольные значения. Учитывая свойства определителя, получим: d₁ =0, d₂ =0, d₃ =0.

Анализ всех возможных случаев расположения трёх плоскостей показывает, что общая бесконечно удалённая точкадля четырёх плоскостей существует только в случае, если векторы:,,,линейно зависимые. Алгебраическое выражение этого факта:

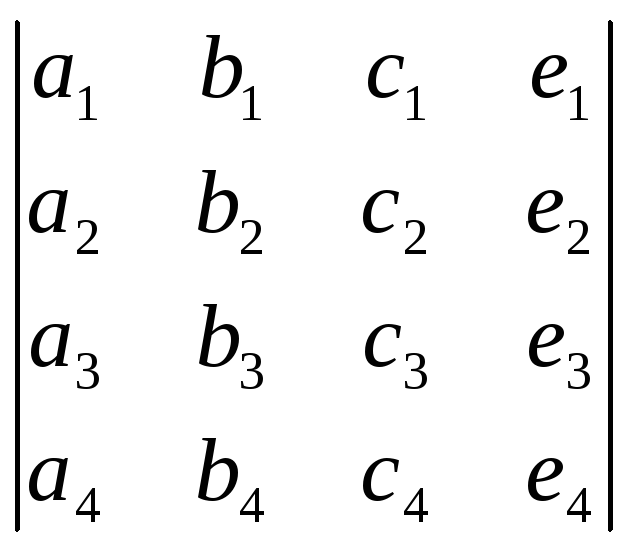=0.

Ответ: анализ и полученные результаты представлены в тексте.

В рассмотренных поясняющих примерах максимально возможно иллюстрируются как теоретические особенности изучаемого материала, так и вычислительные технологии. В следующем параграфе закрепляются образы теоретические и отрабатываются приобретённые навыки вычислений.

☻