§ 3. Решение системы уравнений по правилу Крамера.
При
изучении свойств определителей
-го
порядка были получены формулы Крамера.
Остаётся только уточнить, что
рассматривается частный случай системы
линейных уравнений, когда уравнений
столько же, сколько и неизвестных. В
этом случае система записывается в
виде:
(3)
где
коэффициенты
,
;
–
вещественные числа;
,
–
искомые
неизвестные;
,
–
вещественные числа, их называют:
свободные
члены.
Числа:
,
считаем заданными.
Системе
уравнений соответствуют: матрица
системы
(составлена из коэффициентов при
неизвестных), матрице соответствует
определитель:
=
,
=
.
Замечание:
решение
системы уравнений с применением формул
Крамера не предполагает построения и
использования расширенной матрицы
.
Было
показано, что если
,
то для записи решений системы уравнений
(3) можно использовать формулы
Крамера:
,
,
где:
=
.
Формулы
,
,
определяют единственное
решение, причем не
нулевое,
так как по условию в правой части (3)
имеются не
равные нулю
bi.
Трудоемкость применения правила Крамера оценивают трудоемкостью вычисления (n+1)-го определителя n-го порядка. Достоинство метода в том, что в записи решения системы используются только коэффициенты исходного уравнения. Нередко последнее оказывается важным в теоретических исследованиях.
Ниже рассмотрены примеры решения систем уравнений с использованием формул Крамера.
☺☺
Пример
7–05:
Решить систему уравнений:
по правилу Крамера.
Решение:
1)
Используя коэффициенты левой части
заданной системы линейных уравнений,
запишем определитель: 
=
и вычислим его:
=–3.
2) Вычислим определители:
=
=–3,
=
=–6,
=
=–6,
=
=0.
2)
Применяя формулы Крамера:
,
,
получаем:
=1,
=
=2,
=0.
Ответ: решение: (1,2,2,0).
Пример
7–06:
Решить систему уравнений:
по правилу Крамера.
Решение:
1) Запишем
систему уравнений в стандартной форме:
и
составим определитель: 
=
,
его величина:
=–18·14.
2) Вычислим определители:
=
=3·18·14,
=
=0,
=
=18·7,
=
=–12·14
→
=–3;
=0;
=–
;
=
.
Ответ:
решение:
.
Пример
7–07:
Решить систему уравнений:
по правилу Крамера.
Решение:
1)
Используя коэффициенты левой части
заданной системы линейных уравнений,
запишем определитель: 
=
и вычислим его:
=0.
Замечание:
так как
=0,
то задание решить
систему уравнений с применением формул
Крамера не выполнима, и автор решения
вправе заявить об этом и далее не
исследовать систему; только
любопытство может подвигнуть нас на
продолжение!
2) Вычислим определители:
=
0
→ видим:
невозможно. Вычислять
,
,
нет смысла!
Ответ: решений нет.
☻
§ 4. Исследование (решение) системы уравнений в общем случае.
При рассмотрении решения произвольной системы уравнений методом Гаусса отмечалось, что метод Гаусса позволяет провести полное исследованиелюбой системы. Вполне обоснованно, в таком случае, должен восприниматься вопрос: зачем разрабатывать ещё какие-то методы, если специалист уже получил эффективный инструмент для решения любой системы?
Ответить на возникший вопрос помогут наши исходные рассуждения по поводу источника любой системы линейных уравнений: всякая система уравнений отражает реальные процессы, то есть через все свои коэффициентыона есть математическаямодельконкретного процесса. Метод Гаусса хорош там, где специалист не ставит перед собой задачи усовершенствовать процесс, а только наблюдает ситуации эксплуатации готовой системы.
Метод Крамера не портит модель системы: выражает реакцию системы на внешние воздействия через исходные параметры системы. Этим он хорош! Но, его применение ограничивается только частным классом систем уравнений, и это нас не устраивает.
Методы, которые нужны специалисту, должны иметь возможности обоих указанных методов:
▫ обеспечить полное исследование любой системы уравнений;
▫ решение системы уравнений должно сохранять параметры процесса и реализующей их системы.
Итак,
пусть имеем систему
линейных
уравнений с
неизвестными, которые входят во все
уравнения только в 1-й степени:
(1)
где
коэффициенты
,
;
–
вещественные числа;
,
–
искомые
неизвестные;
,
–
вещественные числа, их называют:
свободные
члены.
Числа:
,
считаем заданными.
Системе
уравнений соответствуют: матрица
системы
A
(составлена из коэффициентов при
неизвестных) и расширенная
матрица
(составлена
из всех
ее коэффициентов, включая свободные
члены): 
=
,
=
.
Для
полного исследования системы нам
потребуются ранги этих матриц:
и
.
Если учесть, что в матрице
векторов-столбцов на один больше, чем
в матрице
,
то либо
=
,
либо
=
+1.
|
Теорема: (7.1) |
Система
линейных уравнений
(1) совместна
тогда и только тогда, когда ранги
матриц
|
и
равны, то есть:
=
.
(Теорема
Кронекера-Капелли).
►10.
Обозначим столбцы матрицы
в виде векторов:
,
,...,
,
.
Тогда можем записать линейную комбинацию
этих векторов в виде:
+
+,...,+
=
.
20.
Пусть система (1) совместна, то есть имеет
некоторое решение в виде системы чисел:
(
,
,...,
).
Это значит, что вектор
линейно выражается через систему
векторов:
,
,...,
в виде линейной комбинации: 
+
+,...,+
=
.
Это
значит, что системы векторов
,
,...,
и
,
,...,
,
эквивалентны, следовательно, имеют
равные ранги:
=
.
30.
Пусть теперь
=
.
Это значит, что любая максимальная
линейно независимая система
векторов-столбцов совокупности
,
,...,
остаётся максимальной и в совокупности
векторов:
,
,...,
,
.
Это значит, что можно найти такие числа
(
,
,...,
),
не все равные нулю, что возможна
запись: 
=
+
+,...,+
.
Это
значит, что система чисел: (
,
,...,
)
может быть использована в качестве
решения системы: система совместна!
◄
Замечание: достоинства исследований с применением теоремы Кронекера–Капелли в том, что окончательное решение можно записать через коэффициенты исходной системы.
Практическое использование теоремы Кронекера–Капелли при решении произвольной системы уравнений. Общая схема решения:
A1*:
Вычисляем ранги:
и
для матриц
и
.
Если:
,
то система решений не имеет. Пусть
=
=
.
Это значит, что определился общий для
матриц
и
базовый
минор:
M
.
На этот минор будем ссылаться при
построении общей схемы решения системы.
Замечание: в случае, когда система не имеет решений, учащийся доволен: задание уже выполнено; для специалиста возникшая ситуация сигналит о том, что наблюдение за процессом было некорректным при создании конкретного уравнения-модели и его нельзя учитывать!
A2*:
В системе уравнений оставляем только
те
уравнения-строки, которые попали
в базовый минор:
остальные являются следствием выделенных.
Замечание: помня, что каждое уравнение системы имеет для специалиста особый смысл, стремятся так реализовать алгоритм выделения базового минора, чтобы наиболее интересные для специалиста уравнения попали в базовый минор!
A3*:
В левой части каждого из оставшихся для
дальнейшего решения уравнений оставляем
те
столбцов с неизвестными, которые попали
в базовый минор:
остальные неизвестные объявляем
свободными
и соответствующие столбцы с ними
переносим в правую часть.
Замечание: процесс объявления некоторых неизвестных свободными для специалиста не является случайным: это варьируемые параметры процесса, при помощи которых можно выделять наиболее желательные реализации процесса!
A4*: Находим решения преобразованной системы уравнений, применяя формулы Крамера: определитель преобразованной системы не равен нулю!
A5*: Полученное решение системы называют общим: вычисленные по формулам Крамера неизвестные выражаются через свободные неизвестные. Присваивая свободным неизвестным произвольные значения, получаем частные решения.
Замечание:
отметим ещё раз, что свободных неизвестных
:
их можно воспринимать как число степеней
свободы процесса; вычисляемых неизвестных
–
.
☺☺
Пример
7–08:
Исследовать систему уравнений:
Найти общее решение и одно частное.
Решение:
1). Составим матрицы:
=
,
=
.
2). Найдем ранги
матриц
и
.
Начнём с матрицы системы
.
Не равных нулю миноров 2-го порядка
несколько. Это значит, что
.
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу матрицы
:
-
3
4
1
2
3
6
8
2
5
7
1
9
12
3
10
13
2
1
3
3). Окаймляющие
миноры будем обозначать:
,
где
–
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
=
=4·
–8·
+12·
=m1·(5)–h1·(4)+g1·(1)=4·(5)–8·(4)+12·(1)
=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минорам
,
,
числа:(5),
(4),
(1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=
m2·(5)–h2·(4)+g2·(1)=
3·(5)–6·(4)+9·(1)
=0;
=
=
m3·(5)–h3·(4)+g3·(1)=
3·(5)–7·(4)+13·(1)
=0.
4).
Так как все миноры 3-го порядка
оказались равными нулю, то
=
=2.
Это значит – система совместна.
5). Учитывая
расположение не равного нулю минора,
3-е уравнение отбрасываем и свободными
неизвестными объявляем
и
:
далее применяем правило Крамера:
=1; 
=
=
;
=
=1.
6). Общее решение
системы:
=
=
;
=
=1;
частное решение получим при значениях:
=–1,
=1,
→
=0,
=1.
Ответ:
общее решение:
=
=
;
=
=1;
частное решение: (–1,1,0,1).
Пример
7–09:
Исследовать систему уравнений:
Найти общее решение и одно частное.
Решение:
1). Составим матрицы:
=
,
=
.
2). Найдем ранги
матриц
и
.
Начнём с матрицы системы
.
Не равных нулю миноров 2-го порядка
несколько. Это значит, что
.
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу матрицы
:
-
3
-2
5
4
2
6
-4
4
3
3
1
9
-6
3
2
4
2
1
3
3). Окаймляющие
миноры будем обозначать:
,
где
–
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
=
=(–2)·
–(–4)·
+(–6)·
=m1·(–1)–h1·(–2)+g1·(–1)=(–2)·(–1)–(–4)·(–2)+(–6)·(–1)=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минорам
,
,
числа:(–1),
(–2),
(–1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=
m2·(–1)–h2·(–2)+g2·(–1)=3·(–1)–6·(–2)+9·(–1)=0;
=
=
m3·(–1)–h3·(–2)+g3·(–1)=
2·(–1)–3·(–2)+4·(–1)=0.
4).
Так как все миноры 3-го порядка
оказались равными нулю, то
=
=2.
Это значит – система совместна.
5). Учитывая
расположение не равного нулю минора,
3-е уравнение отбрасываем и свободными
неизвестными объявляем
и
:
далее применяем правило Крамера:
=–1; 
=
=
;
=
=
.
6). Общее решение
системы:
=
=
;
=
=
;
частное решение получим при значениях:
=
=1,
→
=1,
=–1.
Ответ:
общее решение:
=
=
;
=
=
;
частное: (1,1,1,–1).
Пример
7–10:
Исследовать
систему:
Найти
общее и частное решение.
Решение:
1). Составим матрицы:
=
,
=
.
2). Найдем ранги
матриц
и
.
Начнём с матрицы системы
.
Не равных нулю миноров 2-го порядка
несколько. Это значит, что
.
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу матрицы
:
-
2
-1
1
2
3
2
6
-3
2
4
5
3
1
6
-3
4
8
13
9
2
4
-2
1
1
2
1
3
2
1
4
3). Окаймляющие
миноры будем обозначать:
,
где
–
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченного для
окаймления столбца.
Замечание:
догадываемся, что после вычисления 
не нужно переходить к вычислению миноров
,
,
,
а вычислить раньше минор
.
=
=4·
–8·
+13·
=m1·(–2)–h1·(–1)+g1·(0)=4·(–2)–8·(–1)+13·(0)=0.
Замечание:
параметры: m1,h1,
g1
изменяются при переходе к минору 
,
числа: (–2),(–1),
(0) не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=
m2·(–2)–h2·(–1)+g2·(0)=1·(–2)–1·(–1)+2·(0)
= –1≠0.
4). Интуиция
сработала! Так как
≠0,
то теперь будем окаймлять этот минор и
вычислять окаймляющие миноры. Для
удобства поменяем местами строки 3 и 4:
-
2
-1
1
2
3
2
6
-3
2
4
5
3
4
-2
1
1
2
1
1
6
-3
4
8
13
9
2
1
3
=
=(–1)·
–(–3)·
+(–2)·
–
(–3)·
,
или:
=m1·(–6)–h1·(–1)+g1·(0)
–q1·(–1)=(–1)·(–6)–(–3)·(–1)+(–2)·(0)–(–3)·(–1)
=0;
Замечание:
параметры: m1,h1,
g1
изменяются при переходе к минорам 
,
,
числа: (–12),(14),
(0), (–2)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=m2·(–6)–h2·(–1)+g2·(0)
–q2·(–1)=
2·(–6)–6·(–1)+4·(0)–6·(–1)
=0;
=
=
m3·(–6)–h3·(–1)+g3·(0)
–q3·(–1)=
2·(–6)–3·(–1)+1·(0)–9·(–1)
=0.
5). Следует:
=
3. Учитывая расположение не равного нулю
минора, 3-е уравнение отбрасываем и
свободными неизвестными объявляем
и
:
далее применяем
правило Крамера, учитывая, что определитель
системы равен
=–1:
=
=
=
;
=
=
=0;
=
=
=–
.
6). Общее решение
системы:
=
=
;
=
=0;
=
=
;
частное решение получим при значениях:
=1,
=2,
→
=–1,
=0,
=1.
Ответ:
общее решение:
=
=
;
=
=0;
=
=
;
частное: (1,2,–1,0,1).
Пример
7–11:
Исследовать
систему:
Найти
общее и частное решение.
Решение:
1). Составим матрицы:
=
,
=
.
2). Найдем ранги
матриц
и
.
Начнём с матрицы системы
.
Не равных нулю миноров 2-го порядка
несколько. Это значит, что
.
Выделим для окаймления минор (не равен
нулю), расположенный в правом верхнем
углу матрицы
:
-
6
3
2
3
4
5
4
2
1
2
3
4
1
4
2
3
2
1
0
2
2
1
7
3
2
1
3
2
1
4
3). Окаймляющие
миноры будем обозначать:
,
где
–
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченного для
окаймления столбца.
Замечание:
догадываемся, что после вычисления 
не нужно переходить к вычислению миноров
,
,
,
а вычислить раньше минор
.
=
=3·
–2·
+1·
=m1·(1)–h1·(2)+g1·(1)=3·(1)–2·(2)+1·(1)=0.
Замечание:
параметры: m1,h1,
g1
изменяются при переходе к минору 
,
числа: (–2),(–1),
(0) не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=
m2·(–2)–h2·(–1)+g2·(0)=
7·(1)–3·(2)+2·(1)=
3≠0.
4). Учитывая d21 ≠ 0, переставим строки 3 и 4 для продолжения окаймления:
-
6
3
2
3
4
5
4
2
1
2
3
4
2
1
7
3
2
1
1
4
2
3
2
1
0
2
1
3
=
=3·
–2·
+1·
–2·
,
или:
=m1·(12)–h1·(15)+g1·(0)
–q1·(3)=3·(12)–2·(15)+1·(0)–2·(3)
=0.
Замечание:
параметры: m1,h1,
g1
изменяются при переходе к минорам 
,
,
числа: (12),(15),
(0), (3)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
=
=
m2·(12)–h2·(15)+g2·(0)
–q2·(3)=6·(12)–4·(15)+2·(0)–4·(3)
=0;
=
=
m1·(12)–h1·(15)+g1·(0)
–q1·(3)=5·(12)–4·(15)+1·(0)–0·(3)
=0.
5). Следует:
=
3. Учитывая расположение не равного нулю
минора, 3-е уравнение отбрасываем и
свободными неизвестными объявляем
и
:
далее применяем
правило Крамера, учитывая, что определитель
системы равен
=3:
=
=
=
=
;
=
=
=
=
;
=
=
=
=
.
4). Общее решение
системы: x3=
(4x1+2x2);
x4= –
;
x5=
;
частное решение получим при значениях:
x1=1,x2
= 1 →x3=2,x4= –8,x5=4.
Ответ: общее
решение: x3=
(4x1+2x2);
x4= –
;
x5=
;
частное решение: (1,1, 2,–8,4).
Пример
7–12:Решить систему
линейных уравнений:
методом Гаусса. Общее решение не должно
содержать дробей.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
10
23
17
44
25
10
23
17
44
25
15
35
26
69
40
5
12
9
25
15
25
57
42
108
65
=(1)→
0
-1
-1
-5
0
=(2)→
30
69
51
133
95
0
0
0
1
20
-
10
23
17
44
25
10
23
17
44
25
0
1
1
6
5
0
1
1
6
5
0
-1
-1
-5
0
=(3)→
0
0
0
1
5
0
0
0
1
20
0
0
0
0
15
Выполнены операции: (1): [R4]–[R1]·3; [R3]–[R2]–[R1]; [R2]–[R1]. (2): [R2]·2–[R1];. (3): [R3]+[R2]; [R4]–[R3].
2). Получены результаты: система несовместна, так как уравнение-4 невыполнимо.
Ответ: система несовместна.
Пример
7–13:Исследовать
совместность и найти общее решение
системы линейных уравнений в зависимости
от значения параметра
:
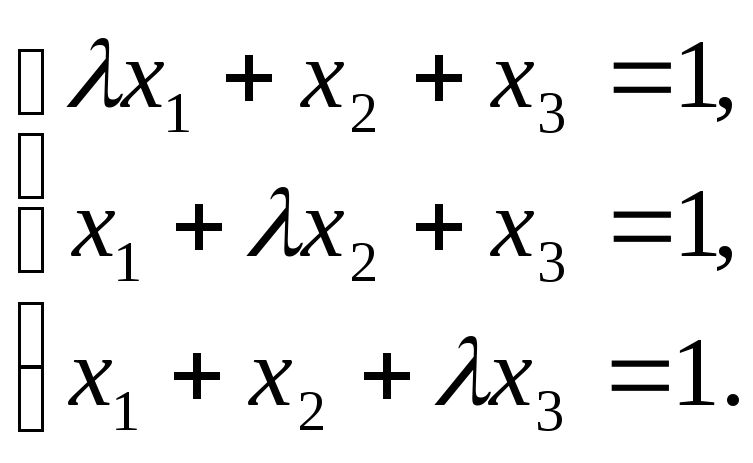
Решение:
1) . Применим пошаговый процесс метода Гаусса:
-
λ
1
1
1
0
1- λ
1- λ 2
1- λ
1
λ
1
1
=(1)→
0
λ -1
1- λ
0
=(2)→
1
1
λ
1
1
1
λ
1
-
0
1
1+ λ
1
1
1
λ
1
0
-1
1
0
=(3)→
0
-1
1
0
=(4)→
1
1
λ
1
0
0
2+ λ
1
Выполнены
операции:
(1):
[R1]–[R3]·
;
[R2]–[R3];
если
–1
= 0, то уравнения [R1]
и [R2]
выполняются при любых значениях
неизвестных. Полученная система
эквивалентна одному уравнению с
неизвестными
,
,
.
(2):
если
–1≠
0, делим [R1],
[R2]
на число 1–
.
(3):
меняем местами строки [R3]
и [R1];
[R3]+[R2]:
если
+2
= 0, то система несовместна, так как
уравнение-3 невыполнимо.
(4):
если
+2≠
0, то вычисляем неизвестные:
,
,
.
2). Получены результаты:
▫ система имеет
бесчисленное множество решений, если
–1
= 0;
▫ если
–1≠
0, система имеет определённое решение:
=
=
=
,
если
–2≠
0, и не имеет решения при
–2
= 0.
Ответ: подробно показано в пункте 2).
Пример
7–14:Исследовать
совместность и найти общее решение
системы линейных уравнений в зависимости
от значения параметра
:
Решение:
1) . Применим пошаговый процесс метода Гаусса:
-
λ
1
1
1
1
0
1- λ
1- λ
1- λ2
1- λ
1
λ
1
1
1
0
λ-1
0
1- λ
0
1
1
λ
1
1
=(1)→
0
0
λ-1
1- λ
0
=(2)→
1
1
1
λ
1
1
1
1
λ
1
-
0
1
1
1+ λ
1
1
1
1
λ
1
0
-1
0
1
0
0
-1
0
1
0
0
0
-1
1
0
=(3)→
0
0
-1
1
0
=(4)→
1
1
1
λ
1
0
0
0
3+λ
1
Выполнены
операции:
(1):
[R1]–[R4]·
;
[R2]–[R4];
[R3]–[R4];
если
–1
= 0, то уравнения [R1],[R2]
и [R3]
выполняются при любых значениях
неизвестных. Полученная система
эквивалентна одному уравнению с
неизвестными
,
,
,
.
(2):
если
–1≠
0, делим [R1]
, [R2]
, [R3]
на число 1–
.
(3):
меняем местами строки [R3]
и [R1];
[R4]+[R3]+[R2]:
если
+3
= 0, то система несовместна, так как
уравнение-4 невыполнимо.
(4):
если
+3≠
0, то вычисляем неизвестные:
,
,
,
.
2). Получены результаты:
▫ система имеет
бесчисленное множество решений, если
–1
= 0;
▫ если
–1≠
0, система имеет определённое решение:
=
=
=
=
,
если
+3≠
0, и не имеет решения при
+3
= 0.
Ответ:подробно показано в пункте 2).
Набор поясняющих Примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений участвующих величин.
☻