§ 2. Решение системы уравнений методом Гаусса.

Самым простым методом решения любой системы линейных уравнений является метод Гаусса: не требует никаких предварительных знаний о системах линейных уравнений, достаточно знать операции сложения и умножения чисел и сразу приступать к поиску решений.

Метод Гаусса называют часто методом последовательного исключения неизвестных. Для реализации этого метода удобно оперировать не с исходной записью системы в виде (1), а с матрицей коэффициентов системы:

, (2)

её принято называть расширенной матрицей системы уравнений.

Метод Гаусса заключается в последовательном применении к строкам матрицы эквивалентных преобразований, приводящих эту матрицу к трапецоидальному или треугольному (в частном случае) виду. В результате реализации метода получим:

▫ система уравнений будет несовместной, если в процессе преобразований получается уравнение, в котором коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля; если же такое уравнение не встретим, то система будет совместной;

▫ если система совместной, то она будет определенной, если она приводится к треугольному виду, и неопределенной, если приводится к трапецоидальному виду.

В основном метод применяют в тех случаях, когда не предполагается исследование технической системы: нужна лишь оценка (подтверждение) реакции системы на конкретные внешние воздействия.

Трудоемкость метода Гаусса оценивают трудоемкостью вычисления одного определителя -го порядка.

Рассмотренные ниже примеры решения систем уравнений с использованием метода Гаусса достаточно полно иллюстрируют его возможности.

☺☺

Пример 7–01:Решить систему линейных уравнений: методом Гаусса.

Решение:

1). Применим пошаговый процесс метода Гаусса:

1	1	-6	-4	6			1	2	-3	0	3
3	-1	-6	-4	2			0	-7	3	-4	-7
2	3	9	2	6	=(1)→		0	-1	15	2	0	=(2)→
3	2	3	8	-7			0	1	3	4	-3

1	2	-3	0	3			1	2	-3	0	3
0	-3	3	0	-5			0	0	0	8	-12
0	-1	15	2	0	=(3)→		0	-1	15	2	0	=(4)→
0	0	6	2	-1			0	0	6	2	-1

Выполнены операции: (1): [R4]–[R2]; [R4] делим на 3; [R1]–[R4]; [R2]–[R1]·3; [R3]–[R1]·2. (2): [R2]+[R4]; [R2] делим на 2; [R4]+[R3]; [R4] делим на 3. (3): [R2]–[R3]·3; [R2]+[R3]·7. (4): получение результата.

2). Получены результаты: - система совместна;

- ранг системы равен 4 → решение системы единственно.

3). Из уравнения [R2] следует:=; далее из уравнения [R2]: 6=, откуда вычисляем:x₃= ;из уравнения [R3]: =, откуда вычисляем:= 2; из уравнения [R1]: =, откуда вычисляем:=0.

Ответ: (0, 2, , –).

Пример 7–02:Решить систему линейных уравнений: методом Гаусса.

Решение:

1). Для уменьшения коэффициентов матрицы, примем: ;;и применим пошаговый процесс метода Гаусса:

3	6	5	6	4	14			1	1	1	1	1	3
5	9	7	8	6	18			1	3	1	3	2	2
6	12	13	9	7	32	=(1)→		1	3	6	1	1	14	=(2)→
4	6	6	5	4	16			0	-4	-2	-5	-2	-6
2	5	4	5	3	11			2	5	4	5	3	11

1	1	1	1	1	3			1	1	1	1	1	3
0	2	0	2	1	-1			0	0	0	-2	-1	-3
0	2	5	0	0	11	=(3)→		0	0	5	-4	-2	9	=(4)→
0	-4	-2	-5	-2	-6			0	-1	0	-2	-1	-1
0	3	2	3	1	5			0	0	2	-3	-2	2

1	1	1	-1	0	0			1	1	1	-1	0	0
0	0	0	-2	-1	-3			0	0	0	0	5	-5
0	0	1	0	1	2	=(5)→		0	0	1	0	1	2	=(6)→
0	-1	0	0	0	2			0	-1	0	0	0	2
0	0	0	-1	-3	1			0	0	0	-1	-3	1

Выполнены операции: (1): [R1]–[R5]; [R3]–[R2]; [R2]–[R4]; [R4]–[R5]·2. (2): [R5]–[R1]·2; [R3]–[R1]; [R2]–[R1]. (3): [R4]+[R5]; [R2]+[R4]·2; [R3]+[R4]·2; [R5]+[R4]·3. (4): [R3]–[R5]·2; [R5]–[R3]·2; [R4]–[R2]; [R3]+[R2]; [R1]+[R2]; [R5]–[R2]·3. (5): [R2]–[R5]·2. (6): раскрываем таблицу и вычисляем все неизвестные.

2). Получены результаты: - система совместна;

- ранг системы равен 5 → решение системы единственно.

3). Из уравнения [R4] следует:=–2; далее из уравнения [R2]: 5=–5, откуда вычисляем:=–1; из уравнения [R3]: =, откуда вычисляем:=3; из уравнения [R5]: =, откуда вычисляем:=2. ; из уравнения [R1]: =, откуда вычисляем:=0.

4). Учитывая обозначения переменных: ;;, получаем решение заданной системы уравнений и записываем ответ.

Ответ: = .

Пример 7–03:Решить систему линейных уравнений: 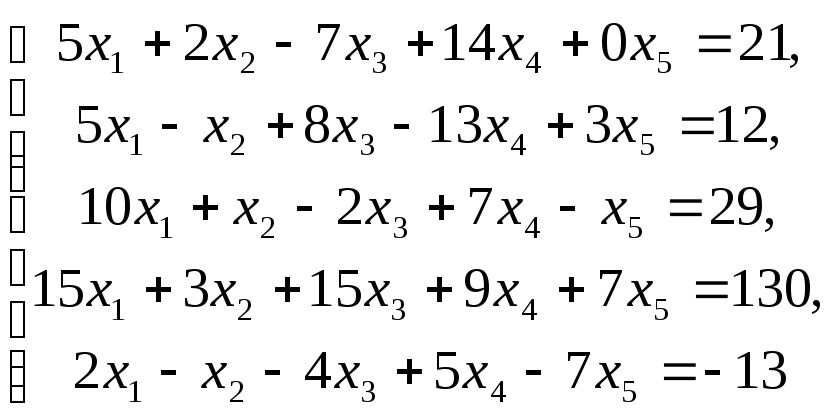методом Гаусса.

Решение:

1). Применим пошаговый процесс метода Гаусса:

5	2	-7	14	0	21			5	2	-7	14	0	21
5	-1	8	-13	3	12			0	-3	15	-27	3	-9
10	1	-2	7	-1	29	=(1)→		0	3	-18	33	-7	5	=(2)→
15	3	15	9	7	130			0	3	9	15	5	89
2	-1	-4	5	-7	-13			2	-1	-4	5	-7	-13

1	4	1	4	14	47			1	4	1	4	14	47
0	-3	15	-27	3	-9			0	1	-5	9	-1	3
0	3	-18	33	-7	5	=(3)→		0	0	-3	6	-4	-4	=(4)→
0	3	9	15	5	89			0	0	24	-12	8	80
0	-9	-6	-3	-35	-107			0	0	-51	78	-44	-80

1	4	1	4	14	47			1	4	1	4	14	47
0	1	-5	9	-1	3			0	1	-5	9	-1	3
0	0	3	-6	4	4	=(5)→		0	0	3	0	0	12	=(6)→
0	0	0	3	-2	4			0	0	0	0	-2	-5
0	0	0	4	-2	7			0	0	0	1	0	3

Выполнены операции: (1): [R4]–[R1]–[R3]; [R3]–[R2]·2; [R2]–[R1]. (2): [R1]–[R5]·2; [R5]–[R1] ·2. (3): [R5]–[R2]·3; [R4]+[R2]; [R3]+[R2]; делим [R2] на (–3). (4): [R5]+[R4]·2; [R4]+[R3]·8; [R5]–[R3]; [R3] умножаем на (–1); [R4] и [R5] делим на 12. (5): R3]+[R4]·2; [R5]–[R4]; [R4]–[R5]·3. (6): раскрываем таблицу и вычисляем все неизвестные.

2). Получены результаты: - система совместна;

- ранг системы равен 5 → решение системы единственно.

3). Из уравнения [R5] следует:=3; далее из уравнения [R4]: =;из уравнения [R3]: =4; из уравнения [R2]: =, откуда вычисляем:=. ; из уравнения [R1]: =, откуда вычисляем:=2.

4). Получили решение заданной системы уравнений: (,,,,) и записываем ответ.

Ответ: (,,,,) =.

Пример 7–04:Решить систему линейных уравнений: методом Гаусса.

Решение:

1). Применим пошаговый процесс метода Гаусса:

9	-3	5	6	4			3	-1	2	2	-1
6	-2	3	4	5	=(1)→		3	-1	0	-10	13	=(2)→
3	-1	3	14	-8			0	0	1	12	-7

3	-1	2	2	-1			3	-1	2	2	-1
0	0	-1	-6	7	=(3)→		0	0	-1	0	7	=(4)→
0	0	0	6	0			0	0	0	6	0

Выполнены операции: (1): [R1]–[R2]; [R2]–[R3]; [R3]–[R1]. (2): [R2]–[R1]; делим строку [R2] на 2; [R3]+[R2]. (3): [R2]+[R3]; [R4]+[R2]. (4): раскрываем таблицу и вычисляем все неизвестные.

2). Получены результаты: - система совместна;

- ранг системы равен 3 → свободная неизвестная =.

3). Из уравнения [R3] следует:=0; далее из уравнения [R2]: =–7; раскрывая уравнение [R1], получаем: ==.

4). Получили общее решение заданной системы, записываем ответ.

Ответ: .

Замечание: любая промежуточная ошибка в цепочке вычислений может быть исправлена от места обнаруженной ошибки.

☻