§ 3. Пучок прямых.

Представляет интерес воспользоваться совокупными свойствами нескольких прямых. Самое простое – это, взяв уравнения двух прямых ,, построить уравнение третьей прямой в виде линейной комбинации заданных прямых:

=, или+=0, (1)

так как инекоторые (произвольные) числа, то записанная линейная комбинация переменных,есть некоторая прямая. Каковы свойства прямой, полученной такимспециальнымспособом?

Из выражения (1) следует, что при значении параметра =0 получается уравнение прямой =, а при значении =0 – уравнение прямой =. Из уравнения (1) следует также, что при любых значениях параметров и прямая будет проходить через точку пересечения прямых ,:

+=0. (2)

Итак, выражение (1) определяет множество прямых, проходящих через точку пересечения двух, заданных, прямых,. Для краткости, будем говорить, что прямыеиопределяют пучок прямых.

Определение: (3.1)

Совокупность всех прямых плоскости, проходящих через одну точку , называется пучком прямых. Точку называют центром пучка.

Замечание: если считать, что параллельные прямые,пересекаются в бесконечно удалённой точке , то запись (1) определит прямую, параллельную прямым,: в таком случае Определение (3.1) можно относить и к параллельным прямым!

Р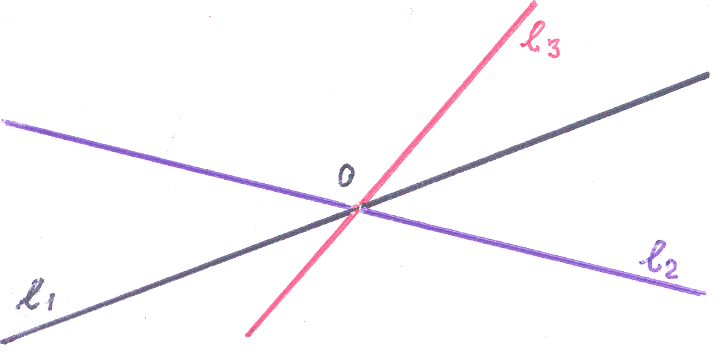ассмотрим более подробно выражение (1) и исследуем совокупные свойства прямых, составляющих пучок.

Если допустить, что одновременно принимаются значения параметров: =0 и =0, то геометрический смысл уравнения (2) пропадает. Поэтому обоснованным будет потребовать: хотя бы один из параметров , не равен нулю!

Отдельно рассмотрим два типа пучков: 1) пучок прямых пересекающихся в конечной точке, 2) пучок параллельных прямых, то есть два случая.

Случай–1: прямые и пересекаются. Это значит, что векторы =,= не коллинеарные, то есть ≠, или ≠0. Выполним тождественные преобразования уравнения (1), приводящие его к виду: =0. (3)

Посмотрим, могут ли, в рассматриваемом случае, коэффициенты при переменных , обратиться в нуль одно­временно: 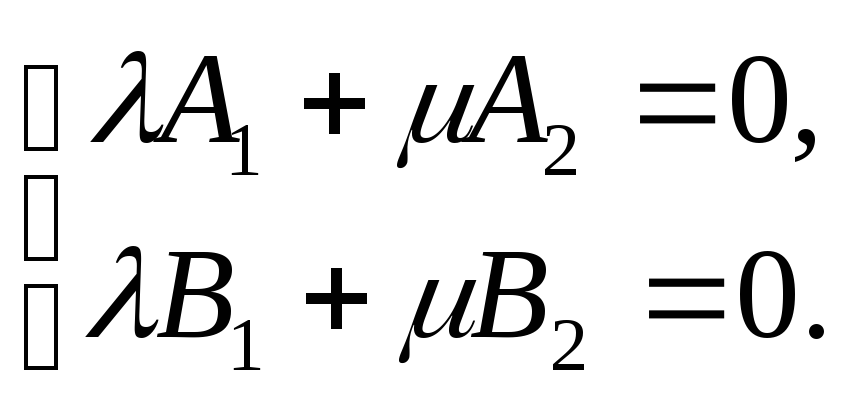(4)

Так как определитель системы уравнений (4): = не равен нулю, то решением системы может быть только нулевое. Это же следует и из уравнения (1). Итак, одновременно параметры и µ в уравнении (1) в нуль не обращаются (это мы увидели и из геометрических соображений).

Пусть и точкой пересечения прямых и является точка . Перепишем уравнение (1) в виде:

+=0, или =0, (5)

учтём в выражении (5): =.

Способы выделения из пучка одной из прямых.

А. Пусть прямая проходит через точку и принадлежит пучку. Используя первое выражение (5), вычислим коэффициент по формуле: = и подставим найденное значение в уравнение:

=0. (6)

Уравнение (6) определяет прямую , проходящую через точку и принадлежащую пучку прямых .

В. Пусть прямая принадлежит пучку и имеет заданный угловой коэффициент . В этом случае необходимо (учитываем в (5) второе выражение): =. Из последнего легко получаем: =. Используя найденное значение , получим уравнение:

=0. (7)

Уравнение (7) определяет прямую , принадлежащую пучку прямых и имеющую угловой коэффициент .

Признак принадлежности трёх прямых одному пучку.

Пусть прямая принадлежит пучку . Тогда уравнение : =0 и уравнение =0 определяют одну и ту же прямую. Составим определитель: 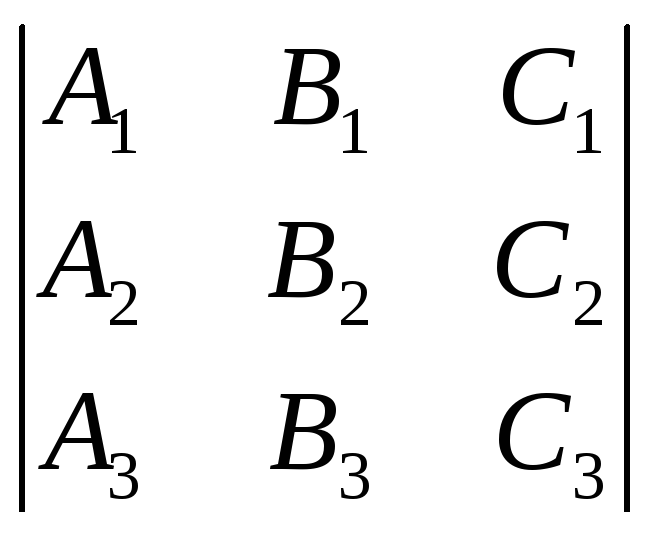==0. (8)

Выражение (8) определяет условие принадлежности трёх прямых одному пучку прямых. Выполнение условия (8) мы будем использовать также для ответа на вопрос: проходят ли прямые через одну точку?

Случай–2: прямые и параллельны, то есть =≠, и =0. В этом случае выражение (1) опреде­ляет пучок параллельных прямых. Для того, чтобы прямая принадлежала пучку и содержала точку , необходимо принять =, =.

Способ выделения из пучка одной из прямых.

Пусть прямая проходит через точку и принадлежит пучку. В этом случае: : =0, где . (9)

Уравнение (9) определяет прямую , проходящую через точку и принадлежащую пучку прямых .

Отметим основные возможности пучка:

▫ конструкция = содержит точку пересечения и , хотя в явном виде часто её не выделяют;

▫ для выделения из пучка прямой с заданными свойствами: проходить через заданную точку, или в заданном направлении требуется определить только одно из названных свойств;

▫ с другими возможностями пучка познакомимся в некоторых из рассматриваемых примеров и задач.

Ниже представлены примеры выделения из пучка одной из прямых с заданными свойствами, а также решение задачи о принадлежности трёх прямых одному пучку.

☺☺

Пример 3–25: Доказать, что прямые:;:и:не проходят через одну точку. Составить уравнение прямой, проходящей через точку пересечения прямых,и параллельной прямой.

Решение:

Способ–1:

1). Так как ≠0, то , пересекаются. Используя условие принадлежности прямых одному пучку, вычислим определитель: =–1≠0. Это значит, что пря­мая l₃ не проходит через точку пересечения прямых ,.

2). Так как прямая параллельна :, то её угловой коэффициент равен: =–. Тогда в уравнении : =0 параметр вычисляем в соответствии с выражениями: ===–. Окончательное выражение для определяется выражением : , или .

Способ–2:

1). Найдем точку пересечения прямых l₁l₂: → =. Легко проверить, что точка l₃.

2). Так как l₄, то удобно воспользоваться уравнением : , где коэффициент =–. После подстановки в выражение значения и координат точки , получим : .

Ответ: прямая : .

Замечание: сравнивая трудоёмкости применённых способов решенияПримера 3–24, видим, что они вполне одинаковы: эффективность использования пучка прямых по сравнению с приёмами элементарной алгебры в этом примере не проявляется.

Пример 3–26: Имеем две прямые:,:. Найти уравнение пря­мой, про­ходящей через точку пересечения,и точку(2, 1).

Решение:

Способ–1:

1). Воспользуемся уравнением пучка : +=0. Пара­метр определим из условия, что точка принадлежит одной из прямых пучка:

. Тогда :–=0, или, после несложных преобразований : .

Способ–2:

1). Найдём точку пересечения прямых l₁l₂: → =(1,2).

2). Найдём уравнение прямой , проходящей через точки и :

→: .

Ответ: прямая : .

Замечание: в этом примере трудоёмкостьСпособа–1существенно ниже!

☻