§ 6. Преобразование координат вектора при переходе к новой базе.

Целью настоящего параграфа является получение расчетных формул для вычисления координат - мерного вектора при переходе от базы к базе .

Вариант-1: используем для записи баз матрицы-столбцы.

Пусть в заданном линейном векторном пространстве имеем базу , а также базы и , причём: =(,,...,)·=·, =(,,...,)·=·, (20)

где , - матрицы-столбцы. Нужно найти матрицу-строку при переходе от базы к базе , если известно: =·, где - матрица перехода от базиса к базису .

Из выражений (20) следуют тождества, связывающие координаты вектора базе с координатами этого вектора в базе : ·=· → ··=· → ·=. Если последнее тождество умножить на матрицу , то получим окончательное выражение:

=·. (21)

Нетрудно заметить, что выражение (21) соответствует (напоминает!) выражению (10) для вычисления матрицы перехода от базы к базе : =·.

Вариант-2: используем для записи баз матрицы -строки.

Пусть в заданном линейном векторном пространстве имеем базу , а также базы и , причём: =(,,…,)·=·, =(,,…, )·=·, (22)

где , - матрицы-строки. Нужно найти матрицу-столбец при переходе от базы к базе , если известно: =·, где - матрица перехода от базиса к базису .

Из выражений (22) следуют тождества, связывающие координаты вектора базе с координатами этого вектора в базе : ·=· → ··=· → ·=. Если последнее тождество умножить на матрицу , то получим окончательное выражение:

=·. (23)

Нетрудно заметить, что выражение (23) соответствует (напоминает!) выражению (12) для вычисления матрицы перехода от базы к базе : =·.

☺☺

Пример 9–20: Пусть имеем трехмерное линейное векторное пространство R с базами и , связанными матричным равенством: =·, где - матрица перехода от базиса к базису . В базе задан вектор =(1,4,-1). Найти координаты вектора в базе , если матрица =.

Решение:

1). Воспользуемся формулой (23): =·, когда , - матрицы-строки, а координаты вектора представляются матрицей-столбцом.

2). Вычисляем матрицу =, любым из освоенных способов.

3). Теперь можем записать: =.

Ответ:строка координат вектора в базеимеет вид: (-13,6,-27) – такая запись удобнее.

☻

Набор поясняющих примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений участвующих величин.

§ 7. Обобщающие примеры по теме: «Линейные векторные пространства»

Набор обобщающих примеров соответствует требованиям «Семестрового плана» при изучении темы: «Линейные векторные пространства». Эти примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих примерах.

☺ ☻ ☺

Пример 1–1277:Показать, что векторы =(1,1,1),=(1,1,2),=(1,2,3) образуют базу пространства, и найти координаты вектора=(6,9,14) в этой базе.

Решение:

Способ-1: использование линейной комбинации векторов.

1). Из координат векторов ,,составим строки матрицы:=и одним из способов вычислим её ранг.

2). Применим элементарные преобразования к заданной матрице:

=(1)→ =(2)→ = (3) →

Операции: (1): [R3]–[R2]; [R2]–[R1]. (2): поменяем местами [R3] и [R2]. (3): анализируем полученный результат.

3). Видим(!): ранг матрицы равен 3. Так как векторы,,- 3-мерные и= 3, то эти векторы можно принять в качестве базы рассматриваемого линейного пространства.

4). Составим линейную комбинацию: =++, где,,- неизвестные числа, неизвестные найдём из системы уравнений:

5). Применим пошаговый процесс метода Гаусса:

1	1	1	6		1	1	1	6		1	0	0	1
1	1	2	9	=(1)→	0	0	1	3	=(2)→	0	0	1	3	=(3)→
1	2	3	14		0	1	1	5		0	1	0	2

Выполнены операции: (1): [R3]–[R2]; [R2]–[R1]. (2): [R1]–[R3]; [R3]–[R2]. (3): читаем решение.

6). Получено решение: =++=++. Координаты векторав базе,,(1,2,3).

Способ-2: использование матричных выражений.

1). Перепишем условие задачи: пусть в заданном линейном векторном пространстве имеем базу . В базе записаны: база и вектор-строка : =·, =·, где , - матрицы-столбцы, - матрица перехода от базы к базису . Нужно найти запись: =·, то есть строку координат вектора в базе .

2). Решение задачи в соответствии с её преобразованным текстом получено нами в виде матричного выражения (21) , с учётом замены на, то есть:=·.

3). В нашем случае: =. Нужно вычислить обратную матрицу.

4). Вычислим обратную матрицу , используя общую формулу для вычисления обратной матрицы: =, где == –1. Так как , то матрица существует.

Вычисляем матрицу = , где = – алгебраическое дополнение к элементу матрицы .

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
1					= –1;					1					= –1;					1					= 1,
		1	2								1		2								1	1
		2	3								1		3								1	2

и вычислим алгебраические дополнения ,,выделенныхминоров:

== –1;= = –1;== 1;

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
		1	1		= –1;						1		1		= 2;						1	1			= –1,
2										2										2
		2	3								1		3								1	2

и вычислим алгебраические дополнения ,,выделенныхминоров:

== –1;= = 2;== –1;

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
		1	1		= 1;						1		1		= –1;						2	4			= 0;
		1	2								1		2								0	1
3										3										3

и вычислим алгебраические дополнения ,,выделенныхминоров:

== 1;= = –1;== 0;

Учитывая результаты вычислений, можем записать: =.

5). Вычисляем: =·=(6,9,14)· =(1,2,3).

Ответ: координаты векторав базе,,(1,2,3).

Пример 2–1281:Имеем систему векторов , где векторы =(1,1,1,1),=(1,2,1,1),= (1,1,2,1) ,= (1,3,2,3), и систему векторов, где векторы =(1,0,3,3),=(-2,-3,-5,-4),=(2,2,5,4) ,=(-2,-3,-4,-4). Доказать, что каждая из систем векторов является базисом. Найти связь координат одного и того же вектора в этих двух базах.

Замечание: учитывая, что трудоёмкость задачи велика, полезно посмотреть в ответ задачника и уточнить, что имеется в виду: задано, нужно найти, или наоборот; видим ответ, определяющий переход:·=, то есть:=·.

Решение:

1). Воспользуемся записями: =·и=·, где,,-матрицы-столбцы. Учитывая исходные данные примера, запишем:

=,=.

2). Убеждаемся, что матрицы и– невырожденные: ||=2, ||=–2.

3). Для рассматриваемого случая, когда ,,-матрицы-столбцы, была получена формула для вычисления матрицы перехода от базык базе: =·.

4). Вычислим обратную матрицу , используя Способ-2. Записываем связку двух матриц , которую обозначим: =. Далее одновременным преобразованием строк этой матрицы, добиваемся преобразования ее левой половины в единичную матрицу . Правая половина матрицы будет иметь вид .

5). Выполним операции: (1): [R2]–[R1]; [R3]–[R1]; [R4]–[R1]. (2): [R4]–[R2]·2; [R4]–[R3].

=(1)= =(2)→ =.

6). Выполним операции: (3): [R4]·; [R1]–[R2] ; [R1]–[R3] ; [R1]–[R4]. Имеем:

=(3)→ =(3) → =.

7). Получена обратная матрица:= ·.

8). Вычислим: =·=··=DP=N, применяя вычислительный шаблон:

Столбец	4	-2	-2	2	Столбец	Столбец	0	2	0	-2	Столбец
	1	0	3	3	4		1	0	3	3	-6
	-2	-3	-5	-4	0		-2	-3	-5	-4	2
	2	2	5	4	2		2	2	5	4	-4
	-2	-3	-4	-4	-2		-2	-3	-4	-4	2

(продолжение таблицы).

Столбец	-1	0	2	-1	Столбец	Столбец	-1	0	0	1	Столбец
	1	0	3	3	2		1	0	3	3	2
	-2	-3	-5	-4	-4		-2	-3	-5	-4	-2
	2	2	5	4	4		2	2	5	4	2
	-2	-3	-4	-4	-2		-2	-3	-4	-4	-2

Из таблицы видим матрицу N:

9). Запишем выражение: =·, или (b₁, b₂, b₃, b₄) =(b'₁,b'₂,b'₃,b'₄)·.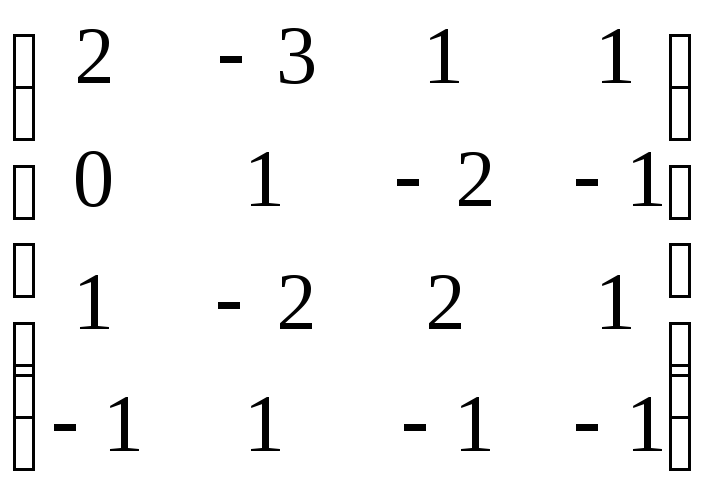

Ответ: получена формула: (b₁, b₂, b₃, b₄) =(b'₁,b'₂,b'₃,b'₄)·.

Пример 3–1285: Имеемn-мерное векторное пространство. Образуют ли подпространство все векторы этого пространства, координаты которых – целые числа?

Решение:

1). Пусть имеем два произвольных вектора : , , координаты которых есть целые числа.

2). Легко заметить, используя правила суммы векторов, что : координаты вектора суммы: = - тоже целые числа.

3). Если, согласно правилу умножения вектора на число, умножим вектор на иррациональное число , например на число , то =, то получаем вектор, координаты которого не есть целые числа → .

4). Следует: выделенная совокупность векторов не является подпространством .

Ответ: не является.

Пример 4–1291: Имеем-мерное векторное пространство. Образуют ли подпространство все векторы этого пространства, координаты которых удовлетворяют линейному уравнению: x₁+ x₂+...+ =0?

Решение:

1). При исследовании решений систем линейных однородных уравнений было отмечено, что множество решений-векторов, порождаемых любой системой линейных однородных уравнений, есть линейное векторное пространство.

2). Так как различных систем линейных однородных уравнений бесчисленное множество, то таких подпространств бесчисленное множество.

3). Следует: выделенная совокупность векторов является подпространством .

Ответ: является.

Пример 5–1297: Доказать, что в- мерном пространстве, где вектор есть строкачисел, все-мерные векторы, у которых первая и последняя координаты равны между собой, образуют линейное подпространство. Найти базис и размерность этого подпространства.

Решение:

1). Воспользуемся моделированием пространства , рассматривая вектора для размерности пространства , например для: =5.

2). Пусть имеем векторы: x=(a, x₂, x₃, x₄, a) и y=(b, y₂, y₃, y₄, b). Легко видеть, что такие векторы являются подпространством пространства .

3). Учитывая определение вектора подпространства, а также свойства операций суммы векторов и умножения вектора на число в пространстве R, запишем совокупность векторов пространства : = (0, 1, 0, 0, 0),

= (0, 0, 1, 0, 0),

= (0, 0, 0, 1, 0),

= (1, 0, 0, 0, 1).

4). Совокупность векторов есть базис подпространства , так как: а) эти векторы независимы; б) с их помощью можно записать любой вектор x подпространства:

x= (a, x₂, x₃, x₄, a) = a ·+ x₂·+ x₃·+ x₄·.

5). Вычисление размерности подпространства в - мерном пространстве не вызывает затруднений: она равна .

Ответ: базис: =(0,1, ...,0),=(0,0,1,...,0), ...,=(0,0,...,1,0), =(1,0,...,0,1); размерность подпространства равна .

Пример 6–1310: Найти размерность и базу линейного подпространства-оболочки, натянутого на систему векторов:= (1,0,0,-1), = (2,1,1,0), = (1,1,1,1), = (1,2,3,4) , =(0,1,2,3).

Решение:

1). Из координат векторов ,,,,составим строки матрицы:=.

2). Для ранга матрицы воспользуемся элементарными преобразованиями матрицы :

1	0	0	-1		1	0	0	-1		1	0	0	-1
2	1	1	0		0	0	0	0		0	0	0	0
1	1	1	1	=(1)→	1	1	1	1	=(2)→	0	1	1	2	=(3)→
1	2	3	4		0	1	2	3		0	0	1	1
0	1	2	3		0	1	2	3		0	0	0	0

Выполнены операции: (1): [R4]–[R3]; [R2]–[R3]; [R2]–[R1]. (2): [R5]–[R4]; [R3]–[R1]; [R4]–[R3]. (3): обрабатываем результаты.

3). Видим(!): ранг матрицы равен 3. Базу подпространства-оболочки могут определять векторы,,. Рассматривая выполненные операции, замечаем, что выделение базы неоднозначно, важно только то, что их ранг не изменится.

Ответ: Базу подпространства-оболочки могут определять векторы ,,.

Пример 7–1313: Найти такую систему уравнений, множество решений которой определяло бы оболочку над векторами:=(1,-1,1,-1,1);=(1,1,0,0,3);=(3,1,1,-1,7);=(0,2,-1,1,2).

Решение:

1). Задача может быть отнесена к классу особо изящных задач! Задача не может быть решена, пока вы не соедините два факта: a*: оболочка – это множество всевозможных линейных комбинаций заданных векторов ,,; b*: так как система уравнений допускает использование линейных комбинаций своих решений, то система уравнений, которую мы должны построить может быть только однородной! Из этого важно продолжение: из условия задачи мы должны понять, что совокупность векторов содержит фундаментальную систему решений искомой системы уравнений. Это ключ к решению задачи!

2). Легко заметить, что ранг системы векторов: ,,, равен 2, причём: =+2 и =–. Это значит, что система векторов: , есть ФСР той системы линейных однородных уравнений, которую мы должны найти.

3). Так как решений в ФСР два, а порядок векторов-решений равен 5, то формирование ФСР , проводилось на основании системы 3-х уравнений с пятью неизвестными:

(A)

коэффициенты этой системы: , ; подлежат определению.

4). Для удобства, обозначим коэффициенты отдельного уравнения из (A) через b₁,b₂,b₃,b₄,b₅. Подставляя в него два решения, получаем систему для определения b₁,b₂,b₃,b₄,b₅:

(B)

5). В системе уравнений (B) в качестве свободных неизвестных удобно приять b₁, b₄, b₅. В этом случае построение ФСР для системы (B) очевидно:

	b2	b3	b1	b4	b5
	-1	-2	1	0	0
	0	1	0	1	0
	-3	-4	0	0	1

6). Три решения , и , или им пропорциональные, определяют систему однородных уравнений (A), для которой векторы , есть ФСР:

множество решений этой системы есть оболочка над векторами ,, то есть подпространство в пространстве векторов .

Ответ: одна из систем уравнений: Отметим: в ответе задачника 1-е уравнение такое же, если из 2-го вычесть 1-е, то получим наше 2-е, если из 1-го выразитьx₁и подставить в 3-е, то получится наше 3-е. Это замечание, должно проиллюстрировать откровенное заявление задачника, что записанодин из вариантовсистемы, дающий (обязательно!)нужную фундаментальную систему решений, используемую для построения линейного векторного подпространства!

Пример 8–1317: Пусть имеем векторное пространствои в нём выделены подпространстваи. Подпространство- оболочка векторов:=(1,2,0,1) и=(1,1,1,0);- оболочка векторов:=(1,01,0) и=(1,3,0,1). Найти размерность суммы=+и пересечения подпространств.

Решение:

1). Нетрудно заметить, что векторы a₁ и a₂, b₁ и b₂ - линейно независимы: координаты не пропорциональны. Это значит, что размерности подпространств: =2, =2.

2). Сумма подпространств построена на векторах: ,,,. Вычислим ранг этой системы векторов:

из векторов ,,,составим матрицу:=и применим элементарные преобразования к заданной матрице:=(1)→ =(2)→ =(3) →

Операции: (1): [R4]–[R1]; [R1]–[R4]·2; [R2]–[R4]. (2): [R3]–[R2]; [R2]–[R1]. 3): анализируем результат.

Видим(!): ранг матрицы равен 3.

3). Так как размерность суммы подпространств равна 3, то, используя выражение: =+–, получаем величину ранга подпространства пересечения: =1.

Ответ: размерность суммы подпространств равна 3, размерность пересечения 1.

Пример 9–1322: Пусть имеем векторное пространствои в нём выделены подпространстваи. Подпространство- оболочка векторов:=(1,1,0,0) ,=(0,1,1,0) ,=(0,0,1,1);- оболочка векторов:=(1,0,1,0) ,=(0,2,1,1) ,=(1,2,1,2). Найти размерность суммы=+и пересечения подпространств.

Решение:

1). Построим матрицы: =, =, Ранги этих матриц: ==3, ==3.

2). Сумма подпространств построена на векторах: ,,,,,. Вычислим ранг этой системы векторов:

из векторов ,,,,,составим матрицу:=и применим элементарные преобразования к заданной матрице:=(1)→ =(2)→

Операции: (1): [R2]–[R1]; [R3]–[R2]; [R4]–[R3]. (2): анализируем результат.

Видим(!): ранг матрицы равен 4.

3). Так как размерность суммы подпространств равна 4, то, используя выражение: =+–, получаем величину ранга подпространства пересечения: =2. Примем также в качестве базы суммы подпространств =+ совокупность векторов: ,,,.

4). Для нахождения базы пересечения подпространств , воспользуемся условием: вектор, принадлежащий , можно записать и через векторы , и векторы : = x₁+ x₂ a₂+ x₃ a₃; и одновременно: = x₄ b₁+ x₅ b₂+ x₆ b₃, что равносильно системе уравнений:

(A)

принимаем в качестве свободных неизвестных: =, = → вычисляем остальные неизвестные: =2–; =; =2–; =–, где и – произвольные постоянные величины. Это общее решение системы уравнений (A).

5). Используя общее решение системы уравнений (A), построим ФСР для этой системы:

	x1	x2	x3	x6	x4	x5
	1	1	1	0	1	1
	2	0	2	1	1	0

Получили векторы базы пересечения : =++=+= (1, 2, 2, 1);

=2+2=+= (2, 2, 2, 2).

Ответ: база суммы подпространств=+совокупность векторов:,,,; база пересечения подпространств - векторы: =++=+= (1, 2, 2, 1); =2+2= += (2, 2, 2, 2).

☻

Вопросы для самопроверки:

1. Что такое линейное пространство?

2. Может ли линейное пространство состоять из а) двух элементов; б) одного элемента; в) 100 элементов?

3. Образует ли линейное пространство множество всех действительных чисел с обычными операциями сложения и умножения на число?

4. Могут ли в линейном пространстве существовать два нулевых элемента?

5. Что понимают под операцией вычитания в линейном пространстве?

6. Справедливо ли равенство 0 = -0?

7. Какие элементы линейного пространства называют линейно независимыми?

8. Можно ли утверждать, что элементы e₁, e₂, … e_n линейного пространства R линейно независимы, если данный элемент x этого пространства единственным образом выражается в виде линейной комбинации указанных n элементов?

9. Пусть в линейном пространстве R имеем n линейно независимых элементов e₁,e₂,…,e_n. Что еще надо потребовать, чтобы указанная совокупность элементов была базисом в данном линейном пространстве?

10. Если среди векторов x,y,z,…,v имеется нулевой вектор, то будут ли эти векторы линейно независимы?

11. Если векторы x,y,z,… линейно зависимы, то можно ли добавлением к ним некоторого количества независимых векторов получить систему независимых векторов?

12. Докажите, что если векторы y,z,…,v линейно независимы, то запись через них вектора x единственна.

13. Может ли матрица C перехода от базиса к быть прямоугольной?

14. Если система векторов базиса представляется в виде матрицы-строки, то строка координат вектора a представляется в виде столбца, и наоборот. Почему?

15. Что значит «размерность векторного пространства»?

16. Что такое «базис линейного пространства»?

17. С какой целью вводится базис в линейном пространстве?

18. Сколько базисов имеется в каждом линейном пространстве?

19. Пусть в линейном пространстве R имеем n линейно независимых элементов e₁,e₂,…,e_n. Что еще надо потребовать, чтобы размерность этого линейного пространства была равна n?

20. Как связаны между собой размерность линейного пространства и число элементов в базисе этого линейного пространства? Является ли это соответствие взаимным?

21. Какова формула перехода от одного базиса к другому в линейном пространстве?

22. Как преобразуются координаты вектора при переходе к новому базису?

23. Что такое «подпространство линейного пространства»?

24. Может ли «подпространство» иметь размерность большую, чем пространство?

25. В определении подпространства М линейного пространства R речь идет о корректности линейных операций на множестве M. Что понимают под этими операциями?

26. Что такое «изоморфизм линейных векторных пространств»?

27. Какова «польза» от применения изоморфизма?

28. Могут ли быть изоморфными 3-мерное и 2-мерное векторные пространства?

29. Что такое «подпространство линейного пространства»?

< * * * * * >