§ 3. Матрица перехода от базы к базе в - мерном векторном пространстве.

Прежде, чем приступить к исследованию матрицы перехода от одной базы к другой, ещё раз отметим, что в пространстве баз бесконечно много! Поэтому определение матрицы перехода от одной базы к другой задача практическая.

Полезно рассмотреть простой пример. Его важность в том, что он отображает традиционные формы записи векторов в тексте: одна запись за другой, строка за строкой...

☺☺

Пример 9–12:Пусть имеем выражения, определяющие переход от базы к базе:=+2и=3+4. Используя операции алгебры матриц, представить переходот базы к базев виде матричного выражения.

Решение:

1). Запишем матрицу, которая компактно и максимально наглядно записывает условие задачи:

==·===·.

2). Из полученной записи следует: если использовать изображение базы в виде столбца, превращение текста задачи в алгебраические выражения максимально удобно и выразительно.

Ответ: = ·, где матрица =.

Замечание: в рассмотренном примере специально не рассматривается вариант изображения матриц для баз и в виде строк: получая все окончательные матричные выражения для случая использования матриц-столбцов, мы легко перепишем их для случая использования матриц-строк, сославшись на соответствующие теоремы.

☻

Пусть в линейном векторном пространстве одновременно рассматриваются две системы векторов: e= (e₁,e₂,…,e_n) и e′= (e′₁,e′₂,…,e′_n), причём обе являются линейно независимыми и приняты в качестве баз пространства .

Учитывая теорему 9.1, для каждого из векторов ,,…, можем записать линейную комбинацию:

, (6)

где , ,…,, - координаты вектора e′_j в базисе e= (e₁,e₂,…,e_n).

Учитывая Пример 9–09 и замечание к нему, превратим совокупность строк (6) в матричное выражение:

==·=·, (7)

Полученный результат (7) вполне законченный для рассматриваемого варианта изображения баз и в виде матриц-столбцов. А если используются матрицы-строки? Как изменится матричное выражение?

Чтобы записать матричное выражение для случая матриц-строк, достаточно вспомнить теорему (нами доказанную!): если известно произведение матриц , то для нахождения транспонированной матрицы нужно вычислить произведение , где матрица получена транспонированием матрицы , матрица – транспонированием матрицы .

В нашем случае матрица-столбец транспонированием превращается в матрицу-строку. Это значит, что вариант с использованием матриц-строк баз учитывается выражением:

e′= (,,…, ) =(,,…,)·=·. (8)

Замечание: для исследования технологического процесса инженер использует ту форму записи матричных уравнений, которая кажется ему более удобной: инженерный результат исследований от этого не изменится.

Для дальнейших обобщений рассматриваемой задачи определения матрицы перехода от одной базы к другой нам потребуется теорема:

Теорема: (9.2)

Пусть имеем базы и линейного векторного пространства . Пусть есть матрица перехода от базы к базе . Тогда матрица - невырожденная, то есть её определитель не равен нулю, и существует обратная матрица для матрицы .

►Допустим, что матрица вырожденная, то есть её определитель равен нулю. Это значило бы, что ранг матрицы меньше и её строки зависимы. Из выражения (7) легко видеть, что в таком случае система векторов зависима. Это противоречие, так как по условию система векторов есть база, то есть система векторов ,,…, независима. Утверждение теоремы доказано. ◄

Теперь мы можем получить такое обобщение рассматриваемой задачи, которое позволит решать любые задачи, в которых требуется найти связь между двумя произвольными базами линейного пространства .

Вариант-1: используем для записи баз матрицы-столбцы.

Пусть в заданном линейном векторном пространстве имеем базу , а также базы и , причём: =·, =·, (9)

где ,, - матрицы-столбцы. Нужно найти матрицу перехода от базы к базе .

В соответствии с теоремой 9.2, матрица – невырожденная, и существует обратная матрица . Используя выражения (9), запишем:

=· → =··=·. (10)

Это значит, что матрица перехода от базы к базе есть матрица: =·.

Вариант-2: используем для записи баз матрицы-строки.

Для записи матричных выражений рассматриваемого случая, вспомним теорему о транспонировании произведения двух матриц:

имеем произведение: =· → получаем: =.

Тогда, выражения, используемые для получения матрицы перехода от базы к базе , принимают вид: =·, =·, (11)

где ,, - матрицы-строки (для удобства записи штрихи транспонирования не показываем). Используя выражения (11), запишем:

=· → =··=·. (12)

Это значит, что матрица перехода от базы к базе есть матрица: =·.

☺☺

Пример 9–13:Как поменяется матрица перехода от базиса к базису, если:

1) поменять местами два вектора базиса ;

2) поменять местами два вектора базиса ;

3) записать векторы базисов и в обратном порядке.

Решение:

1). Воспользуемся преобразованием: ==·=·, где - матрица перехода от базиса к базису .

2). Построим модель, которая используемое преобразование: =·делает особенно наглядным для ответа на поставленные вопросы:

		e1	e2	e3	e4	e5	e6
		↓	↓	↓	↓	↓	↓
e′1	←
e′2	←
e′3	←
e′4	←
e′5	←
e′6	←

3). Если поменять местами два вектора базиса e=(,,,,,), то (видим) в матрице должны поменяться местами соответствующие два столбца.

4). Если поменять местами два вектора базиса e'=(,,,,,), то (видим) в матрице должны поменяться местами соответствующие две строки.

5). Если записать векторы базисов и в обратном порядке, то матрицу необходимо подвергнуть преобразованиюцентральной симметрииотносительноцентра квадратаматрицы. Такая модель применена нами при рассмотрении определителей - порядка.

Замечание: рассмотрен вариант решения задачи для случая, когда системы векторов базисовиизображаются в виде столбцов. Аналогично задача решается для систем-строк.

Ответ: в тексте представлены подробные ответы на все три вопроса задачи.

Пример 9–14: Пусть в заданном линейном векторном пространстве имеем базу, а также базыи, причём:=·=·,=·=·,

где ,, - матрицы-строки. Нужно найти матрицу перехода от базы к базе .

Решение:

1). В соответствии с выражениями (11) и (12), матрица перехода определяется произведением: =·.

2). Вычислим обратную матрицу , используя общую формулу для вычисления обратной матрицы: =, где == –3. Так как , то матрица существует.

Вычисляем матрицу = , где = – алгебраическое дополнение к элементу матрицы .

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
1					= –3;					1					= 3;					1					= –3,
		1	1								0		1								0	1
		5	2								3		2								3	5

и вычислим алгебраические дополнения ,,выделенныхминоров:

== –3;= = 3;== –3;

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
		4	3		= 7;						2		3		= –5;						2	4			= 2,
2										2										2
		5	2								3		2								3	5

и вычислим алгебраические дополнения ,,выделенныхминоров:

== 7;= = –5;== 2;

*Выделим миноры:к элементу;к элементу;к элементу:

	1											2											3
		4	3		= 1;						2		3		= –2;						2	4			= 2;
		1	1								0		1								0	1
3										3										3

и вычислим алгебраические дополнения ,,выделенныхминоров:

== 1;= = –2;== 2;

Учитывая результаты вычислений, можем записать: =.

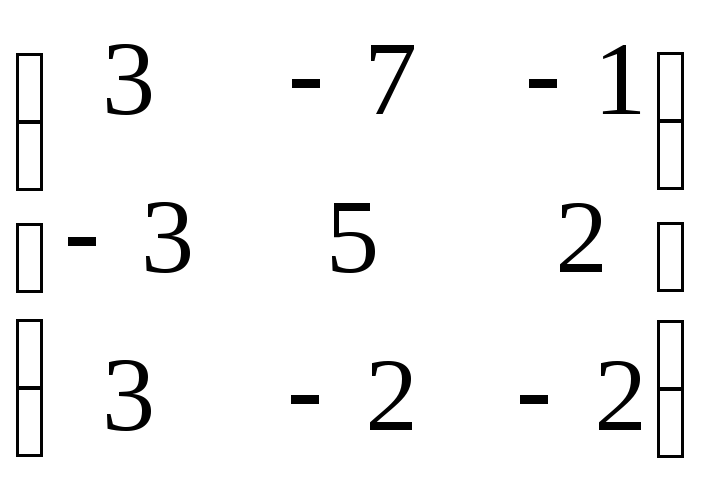3). Вычислим произведение матриц: =·=·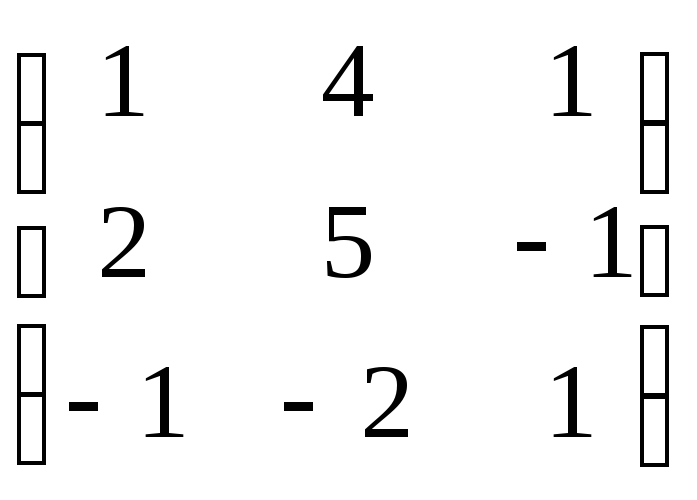=DB=K, применяя вычислительный шаблон:

Столбец	1	2	-1	Столбец	Столбец	4	5	-2	Столбец	Столбец	1	-1	1	Столбец
	3	-7	-1	-10		3	-7	-1	-21		3	-7	-1	9
	-3	5	2	5		-3	5	2	9		-3	5	2	-6
	3	-2	-2	1		3	-2	-2	6		3	-2	-2	3

Из таблицы видим ответ.

Ответ: матрица перехода от базиса к базе есть матрица: .

☻