§ 4. Матричное уравнение.

Формы записи матричных уравнений могут быть трёх видов:

L¹: AX = R; L²: YA = T; L³: = S. (1)

Решение этих уравнений, при условии выполнимости всех используемых операций, можно записать в виде:

P¹: X =R; P²: Y =; P³: =. (2)

Достоинство матричных уравнений: выражения (1) и (2): компактны; при имеющихся записях всех матриц в выражениях (1) удобная реализация вычислений (2) при помощи специальных программ, например, маткад.

Недостаток матричных уравнений:

1). Ограниченная область применения: участвующие в выражениях (1) матрицы: и , должны быть квадратными и невырожденными, то есть , .

2). Низкая наглядность совершаемых вычислений, что может затруднять контакт специалиста с исследуемым процессом.

Следующий пример хорошо иллюстрирует особенности применения матричных уравнений и отмеченные недостатки.

☺☺

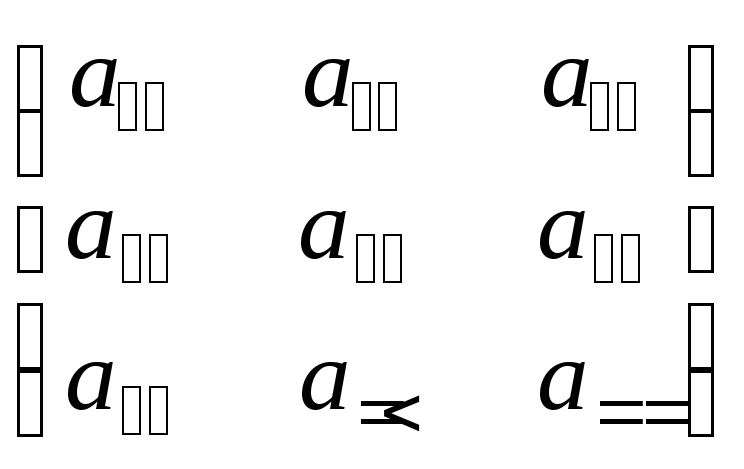Пример 5–04: Пусть имеем матричное уравнение:=. Пусть матрицы =и=– заданы, требуется вычислить матрицу=.

Легко заметить:

1). Используя правило умножения матриц, можем записать два уравнения, эквивалентных заданному уравнению: =и=, что равносильно использованию двух матричных уравнений:=и=.

2). Требование обеспечивает применение правила Крамера для записиединственногорешения, как для уравнения=, так и для уравнения=.

3). Так как для специалиста-исследователя случай единственного решения системы уравнений является малопривлекательным, то это же, с полным правом, отнесём и к матричным уравнениям!

☻

В тех случаях, когда: =0, =0, то есть не существуют матрицы: , , требуются специальные исследования. Некоторые из рассмотренных примеров вполне иллюстрируют случаи, когда матричное уравнение не имеет решений, или имеет их бесчисленное множество.

☺☺

Пример 5–05: Решить матричное уравнение: ·X=.

Решение:

1). Решение ищем в виде: . Воспользуемся общим алгоритмом вычисления обратной матрицы=:

=4, =→=.

2). В матричной форме решение имеет вид: =·=. Умножение матриц проведём, применяя шаблон:

Столбец	12	0	Столбец	Столбец	8	4	Столбец
	4	0	48		4	0	32
	-3	1	-36		-3	1	-20

Использование шаблона помогает отработать алгоритм вычисления произведения матриц и защищает от ошибок в вычислениях.

Замечание: использование вычислительных шаблонов может существенно сократить время вычисления произведения матриц: алгоритм вычислений становится хорошо обозримым и контролируемым!

Ответ:=.

Пример 5–06: Решить матричное уравнение: ·X=.

Решение:

1). Имеем уравнение вида: =, то есть: ·=. Так как=0, то обратной матрицы: не существует, и воспользоваться записьюне можем!

Замечание: вспомним, как проводились исследования решений произвольной системы уравнений 2-го и 3-го порядков в Главе 2 настоящего пособия, и применим полученные там результаты!

2). Перепишем уравнение в виде: =.Так как правая и левая части матричного уравнения матрицы, из условия их равенства можем записать системы уравнений:

3). Принимая и, запишем решение уравнения: .

Ответ:x =, гдеи– произвольные числа.

Пример 5–07: Решить матричное уравнение:X·=.

Решение:

1). Имеем уравнение вида: =, то есть: ·=. Так как=0, то обратной матрицы: не существует, и воспользоваться записьюне можем!

Замечание: воспользуемся вычислительным алгоритмом и результатамиПримера 5–05.

2). Перепишем уравнение в виде: =.Так как правая и левая части матричного уравнения матрицы, из условия их равенства можем записать системы уравнений:

3). Принимая и, запишем решение уравнения: .

Ответ:x =, гдеи– произвольные числа.

Пример 5–08: Решить матричное уравнение: ·X=.

Решение:

1). Имеем уравнение вида: =, то есть: ·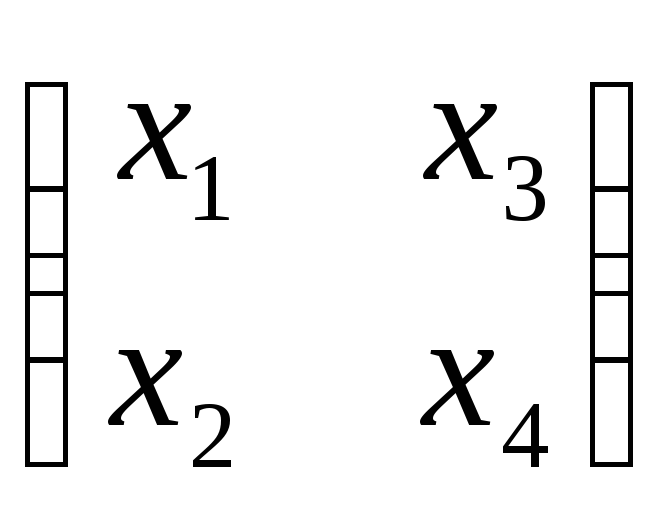=. Так как=0, то обратной матрицы: не существует, и воспользоваться записьюне можем!

Замечание: воспользуемся вычислительным алгоритмом и результатамиПримеров 5–05 и 5–06.

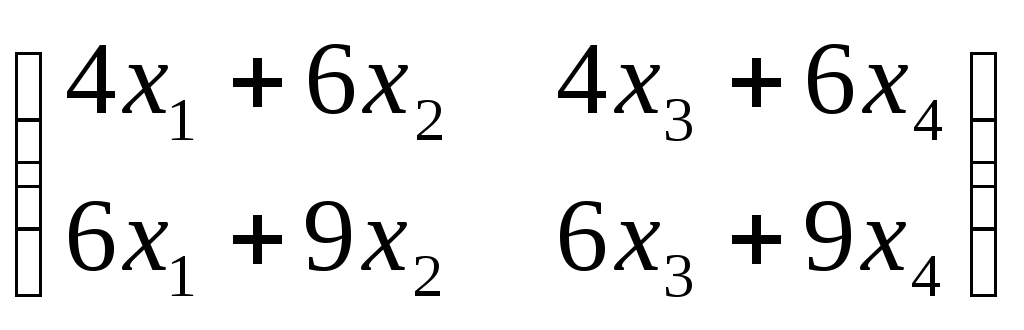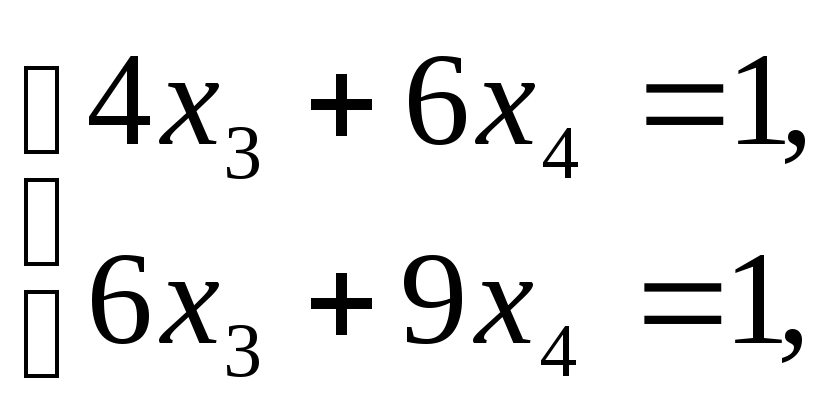2). Перепишем уравнение в виде: =.Так как правая и левая части матричного уравнения матрицы, из условия их равенства можем записать системы уравнений:илиили

3). Видим, обе системы уравнений – противоречивы → исходное матричное уравнение решений не имеет.

Ответ: уравнение решений не имеет.

☻