
Глава 5. Обратная матрица.
В настоящей главе вводится понятие обратная матрица. В определенном смысле этоподражаниечислам: естьумножение, то почему бы не бытьделению? Для чисел деление вводится использованиемединицыиобратного числа, определяющими свойствами которых являются выражения:
▫ для любого числа
![]() существует такоечисло1, что
существует такоечисло1, что![]() ;
число 1 называют единицей;
;
число 1 называют единицей;
▫ для любого числа
![]() существует
существует![]() такое, что
такое, что![]() =1,
где число
=1,
где число![]() называетсяобратнымчислу
называетсяобратнымчислу![]() .
.
Попробуем с матрицами поступить также! А именно: определить матрицу-единицуиобратную матрицу.
§ 1. Единичная матрица.
Для матрицы-единицы
Eпотребуем: для произвольной матрицыAпусть будет выполнено требование:![]() ·
·![]() =
=![]() ·
·![]() =
=![]() .
(1)
.
(1)
Если оценивать выражение (1) формально, то может показаться, что это не более чем обозначение подражания числам. На самом деле, выражение (1) является определяющим при построении обратной матрицы для заданной матрицы A. Верна следующая теорема.
|
Теорема: (5.1) |
Матрицы
|
►Допустим,
выражение
![]() ·
·![]() =
=![]() ·
·![]() =
=![]() выполняется для произвольной матрицы
выполняется для произвольной матрицы
![]() .
Пока не решён вопрос о матрице
.
Пока не решён вопрос о матрице
![]() ,
можно считать, что матрица
,
можно считать, что матрица
![]() должна быть специально построена для
каждой заданной матрицы
должна быть специально построена для
каждой заданной матрицы
![]() .
.
Замечание:
в алгебре матриц была определена операция
умножения матрицы
![]() на число
на число
![]() с выполнением переместительного
свойства:
с выполнением переместительного
свойства:
![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
которое при значении
,
которое при значении
![]() =1
совпадает с выражением (1); этот тривиальный
случай не представляет интереса при
решении задачи построения обратной
матрицы.
=1
совпадает с выражением (1); этот тривиальный
случай не представляет интереса при
решении задачи построения обратной
матрицы.
Из выражения (1) следует:
F1:
матрица![]() ·
·![]() =
C1существует,
то есть умножение матрицы
=
C1существует,
то есть умножение матрицы![]() на
на![]() выполнимо;
выполнимо;
F2:
матрица![]() ·
·![]() =
C2существует,
то есть умножение матрицы
=
C2существует,
то есть умножение матрицы![]() на
на![]() выполнимо;
выполнимо;
F3: матрицыC1иC2равны.
Замечание: предполагается, что умножение матриц определено по правилу строка – столбец: количество столбцов в матрице A равно количеству строк в матрице B.
F1.
Так как возможно составить произведение![]() ·
·![]() ,
то число строк матрицы
,
то число строк матрицы![]() должно быть равным числу столбцов
матрицыA, это отражено
на схеме:
должно быть равным числу столбцов
матрицыA, это отражено
на схеме:
|
|
n |
|
|
|
k |
|
|
|
k | ||||||||||||
|
m |
A |
|
|
n |
E |
|
|
m |
C1 | ||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
• |
|
═ | ||||||||||||||||||
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
F2.
Так как возможно составить произведение![]() ·
·![]() ,
то число строк матрицыAдолжно быть равным числу столбцов
матрицы
,
то число строк матрицыAдолжно быть равным числу столбцов
матрицы![]() ,
это отражено на схеме:
,
это отражено на схеме:
|
|
k |
|
|
|
n |
|
|
|
n | |||||||
|
n |
E |
|
|
m |
A |
|
|
n |
C2 | |||||||
|
|
|
|
| |||||||||||||
|
|
• |
|
═ | |||||||||||||
|
|
| |||||||||||||||
|
|
|
|
| |||||||||||||
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Из представленной
схемы следует: необходимо
![]() =
=![]() ,
так как умножение матриц выполнимо, по
условию.
,
так как умножение матриц выполнимо, по
условию.
F3.
Из условия:
![]() следует→
следует→![]() =
=![]() .
Имеем окончательно: условию (1) могут
удовлетворять только квадратные матрицы
.
Имеем окончательно: условию (1) могут
удовлетворять только квадратные матрицы![]() и
и![]() ,
имеющие одинаковый порядок:
,
имеющие одинаковый порядок:
![]() .◄
.◄
Вопрос об определении
записи матрицы
![]() решает следующая теорема.
решает следующая теорема.
|
Теорема: (5.2) |
Если
матрицы |
►Для
уменьшения громоздкости оформления
доказательства рассмотрим матрицы
размерности (4,4): ![]() =
= ,
,
![]() =
= .
.
1) Запишем условие
![]() ·
·![]() =
=![]() в виде выражения:
в виде выражения:
 ·
· =
= ,
,
откуда следует:
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0.
=0.
так
как последнее равенство выполняется
для любых
чисел (матрица
![]() – произвольная), то необходимо:
– произвольная), то необходимо:
![]() =1,
=1,
![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
так
как элементы матрицы
![]() – произвольные числа. Аналогично
получим:
– произвольные числа. Аналогично
получим:
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0,
=0,
![]() =0,
=0,
![]() =1,
=1,
![]() =0,
=0,
![]() =0;
=0;
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
![]() =1,
=1,
![]() =0;
=0;
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
![]() =1.
=1.
2) Запишем условие
![]() ·
·![]() =
=![]() в виде выражения:
в виде выражения:
 ·
· =
= ,
,
откуда следует:
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0.
=0.
так
как последнее равенство выполняется
для любых чисел (матрица
![]() – произвольная), то необходимо:
– произвольная), то необходимо:
![]() =1,
=1,
![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
так
как элементы матрицы
![]() – произвольные числа. Аналогично
получим:
– произвольные числа. Аналогично
получим:
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0.
=0.
![]() =0,
=0,
![]() =1,
=1,
![]() =0,
=0,
![]() =0;
=0;
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0.
=0.
![]() =0,
=0,
![]() =0,
=0,
![]() =1,
=1,
![]() =0;
=0;
![]() +
+![]() +
+![]() +
+![]() =
=![]() ,
или
,
или
![]() +
+![]() +
+![]() +
+![]() =0.
=0.
![]() =0,
=0,
![]() =0,
=0,
![]() =0,
=0,
![]() =1.
=1.
Замечание:
хотя доказательство теоремы, определяющей
матрицу ![]() ,
демонстрирует её единственность, часто
проводят дополнительное доказательство
единственности
,
демонстрирует её единственность, часто
проводят дополнительное доказательство
единственности ![]() .
.
Допустим, что некоторая матрица E′тоже единичная. Тогда можем записать:
|
E′ E= E′ |
→ E′= |
|
E′ E= E |
В выражениях E′ E= E′иE′ E= Eсущественно используется то, что единичная матрица перестановочна с любой матрицей.◄
Используя операцию умножения матрицы на число, можно определить скалярнуюматрицу:
![]() =
= . (2)
. (2)
Для
скалярной матрицы верно: ![]() =
=![]() =
=![]() =
=![]() ,
что легко проверяется непосредственно
использованием свойств операций
умножения матрицы на число и произведения
матриц.
,
что легко проверяется непосредственно
использованием свойств операций
умножения матрицы на число и произведения
матриц.
Замечание:
если записано матричное выражение:
![]() =
=![]() +2
+2![]() +5,
то всегда имеют в виду, что используется
не число 5, а квадратная матрица 5
+5,
то всегда имеют в виду, что используется
не число 5, а квадратная матрица 5![]() той же размерности, что и у матриц
той же размерности, что и у матриц
![]() и
и![]() .
.

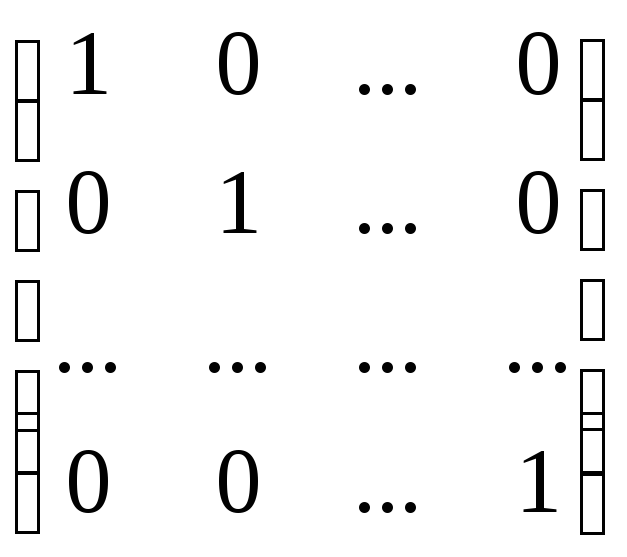 .
Такая
матрица называется единичной.
.
Такая
матрица называется единичной.