
Биполярный транзистор
Шумовая
эквивалентная схема биполярного
транзистора, работающего в нормальном
активном режиме, показана на рис.3.8.
Малосигнальная эквивалентная схема
биполярного транзистора дополнена
источниками среднеквадратичного
отклонения шума:
![]() - тепловой
шум сопротивления тела базы диода;
- тепловой
шум сопротивления тела базы диода;
![]() - дробовой
шум коллекторного перехода;
- дробовой
шум коллекторного перехода;
![]() - суммарный
дробовой и фликкер шум перехода
эмиттер-база;
- суммарный
дробовой и фликкер шум перехода
эмиттер-база;
![]() - дифференциальная входная проводимость
базы;
- дифференциальная входная проводимость
базы;
![]() - дифференциальная выходная проводимость
коллектор-эмиттер;
- дифференциальная выходная проводимость
коллектор-эмиттер;
![]() -
дифференциальная прямая передаточная
проводимость транзистора.
-
дифференциальная прямая передаточная
проводимость транзистора.

.Мдп транзистор
Малосигнальная эквивалентная схема МДП транзистора, работающего в пологой области, с источниками шума показана на рис.3.9.
Затвор![]()

![]() -
тепловой и фликкер шум стока;
-
тепловой и фликкер шум стока;
![]() - ток
стока;
- ток
стока;
![]() - передаточная проводимость идеального
транзистора (крутизна МДП транзистора
в рабочей точке);
- передаточная проводимость идеального
транзистора (крутизна МДП транзистора
в рабочей точке);
![]() - дифференциальная выходная проводимость
сток-исток.
- дифференциальная выходная проводимость
сток-исток.
Идеальные конденсаторы (конденсаторы без утечек), а также идеальные катушки индуктивности (без сопротивления), не являются источниками шумов. Индуктивности, выполненные как резистивные спирали, имеют шумовые источники резисторов.
9 Предположим, что известно
среднеквадратичное отклонение шумового
напряжения на входе аналогового
устройства, обладающего коэффициентом
усиления по напряжению
Предположим, что известно
среднеквадратичное отклонение шумового
напряжения на входе аналогового
устройства, обладающего коэффициентом
усиления по напряжению
![]() (рис.3.10). Как рассчитать выходное шумовое
напряжение?
(рис.3.10). Как рассчитать выходное шумовое
напряжение?
Между квадратом шумового напряжения (среднеквадратичным отклонением) и спектральной плотностью существует связь
![]() тогда
тогда
![]()
Учитывая,
что аналоговое устройство обладает
комплексным коэффициентом усиления
![]() ,
для шумового напряжения на выходе будем
иметь
,
для шумового напряжения на выходе будем
иметь
![]()
Тогда
спектральная плотность выходного
сигнала имеет вид:
![]() Квадрат шумового напряжения можно
рассчитать путем суммирования спектральной
плотности по каждой из шумовых
составляющих, т.е.
Квадрат шумового напряжения можно
рассчитать путем суммирования спектральной
плотности по каждой из шумовых
составляющих, т.е.
![]()
Пример
1.
Расчет шума от
двух источников (рис.3.10). Пусть
![]() ,
,
![]()
Если
источники не коррелированны, тогда
![]()
Пример 2. Расчет шумового напряжения для усилителя на БТ.
Э лектрическая
схема простейшего биполярного усилителя
с нагрузочным сопротивлением RL
и резистором смещения RS
приведена на
рис.3.11.
Малосигнальная эквивалентная схема с
шумовыми источниками имеет вид, показанный
на рис.3.12.
лектрическая
схема простейшего биполярного усилителя
с нагрузочным сопротивлением RL
и резистором смещения RS
приведена на
рис.3.11.
Малосигнальная эквивалентная схема с
шумовыми источниками имеет вид, показанный
на рис.3.12.
где
![]() - тепловой шум от резистора смещения
RS;
- тепловой шум от резистора смещения
RS;
![]() - тепловой шум от резистора нагрузки
RL;
- тепловой шум от резистора нагрузки
RL;
![]() -
тепловой шум от базового резистора
нагрузки;
-
тепловой шум от базового резистора
нагрузки;
 -
дробовой и фликкер шум перехода
база-эмиттер;
-
дробовой и фликкер шум перехода
база-эмиттер;
![]()
 -
дробовой шум коллекторного перехода.
-
дробовой шум коллекторного перехода.
Чтобы рассчитать квадрат выходного шумового напряжения, воспользуемся правилом суперпозиции. Рассчитаем вклад от каждого независимого шумового источника на выход.
Вклад U1 от шумового источника US составит:
![]() ,
где
,
где
 - параллельное
включение дифференциального сопротивления
базы
- параллельное
включение дифференциального сопротивления
базы
![]() и
и
![]() .
Тогда вклад в выходное напряжение от
US
будет равен Uout1 = gmRLU1,
следовательно, квадрат шумового
напряжения на выходе от US
имеет вид:
.
Тогда вклад в выходное напряжение от
US
будет равен Uout1 = gmRLU1,
следовательно, квадрат шумового
напряжения на выходе от US
имеет вид:
 Подобный расчет можно провести для
источников Uб2
и iб2
тогда будем иметь:
Подобный расчет можно провести для
источников Uб2
и iб2
тогда будем иметь:


Вклад
в выходное напряжение от выходных
источников шума составит:
![]()
![]()
Суммируя
вклады от всех источников, в результате
получим выражение для квадрата выходного
напряжения шума.
![]()

![]()
где![]() .
.
П олученный
результат можно интерпретировать
электрической схемой, показанной на
рис.3.13 содержащей только один шумовой
источник
олученный
результат можно интерпретировать
электрической схемой, показанной на
рис.3.13 содержащей только один шумовой
источник
![]() .
Тогда
.
Тогда
![]() ,
а также транзистор свободны от шума.
,
а также транзистор свободны от шума.
В
результате квадрат выходного напряжения
будет равен: , где
, где
![]()
![]()
Э та
зависимость имеет график, который
представлен на рис.3.14. Следует отметить,
что возрастание шумового напряжения
слева связано с возрастанием шума типа
та
зависимость имеет график, который
представлен на рис.3.14. Следует отметить,
что возрастание шумового напряжения
слева связано с возрастанием шума типа
![]() ,
а возрастание шума справа объясняется
спадом усиления транзистора в зависимости
от увеличения частоты.
,
а возрастание шума справа объясняется
спадом усиления транзистора в зависимости
от увеличения частоты.
10
Кусочно-линейная
аппроксимация основана на приближенной
замене реальной ВАХ отрезками прямых
линий с разными наклонами. Примером
может служить входная характеристика
биполярного транзистора  (4.3)
Для тока коллектора вводится понятие
передаточной проводимости
(4.3)
Для тока коллектора вводится понятие
передаточной проводимости ![]() (4.4)
Тогда для коллекторного тока будем
иметь следующее выражение:
(4.4)
Тогда для коллекторного тока будем
иметь следующее выражение: ![]() (4.5)
где
(4.5)
где
![]() -
напряжение насыщения база-эмиттер,
-
напряжение насыщения база-эмиттер,
![]() - напряжение на нелинейном элементе.
- напряжение на нелинейном элементе.
Способ
степенной
аппроксимации
основан на разложении нелинейной ВАХ
в ряд Тейлора в окрестности рабочей
точки U0
![]() , (4.6)
где
, (4.6)
где
![]() .
.
Примером степенной
аппроксимации является проходная
характеристика полевого транзистора,
![]()
Показательная
аппроксимация это представление ВАХ
нелинейных элементов с помощью
экспоненциальной зависимости вида:
![]() (4.7)
где
(4.7)
где
![]() - ток насыщения,
- ток насыщения,
![]() - тепловой потенциал (при температуре
- тепловой потенциал (при температуре
![]()
![]() ).
).
11 Пусть имеется некая замкнутая электрическая цепь, содержащая источник входного сигнала, нелинейный безинерционный элемент, например диод и резистивную нагрузку (рис.4.4).
Ф орма
входного сигнала задается гармонической
функцией:
орма
входного сигнала задается гармонической
функцией:
![]() Имея
ВАХ нелинейного элемента, легко графически
получить сигнал на нагрузке RL.
Из графика на рис.4.4 видно, что форма
сигнала на выходе существенно отличается
от входного сигнала, т.е. произошли его
искажения. Причина искажения связана
с тем, что одинаковым приращениям
напряжения на нелинейном элементе
отвечают разные приращения тока.
Имея
ВАХ нелинейного элемента, легко графически
получить сигнал на нагрузке RL.
Из графика на рис.4.4 видно, что форма
сигнала на выходе существенно отличается
от входного сигнала, т.е. произошли его
искажения. Причина искажения связана
с тем, что одинаковым приращениям
напряжения на нелинейном элементе
отвечают разные приращения тока.
Чтобы
определить состав спектральных
составляющих выходного сигнала,
представим зависимость выходного тока
от времени следующим соотношением: ![]() (4.8)
(4.8)
где
![]() - максимальная
амплитуда входного сигнала;
- максимальная
амплитуда входного сигнала;
![]() – напряжение смещения;
– напряжение смещения;
![]() .
.
Так
как функция (4.8) периодическая с периодом
2,
то ее можно представить в виде ряда
Фурье: ![]() (4.9)
с коэффициентами
(4.9)
с коэффициентами
![]() (4.10)
(4.10)
Так как функция (4.8) четная, то разложение (4.9) будет содержать только косинусоидальные составляющие, т.е.
![]() (4.11)
(4.11)
где
![]() (4.12)
(4.12)
Анализ выражений (4.11) и (4.12) показывает, что:
-
в спектре выходного сигнала содержится бесконечное число гармоник вида
 (или
(или
 ),
где
),
где
 .
. -
амплитуды составляющих гармоник зависят от
 ,
,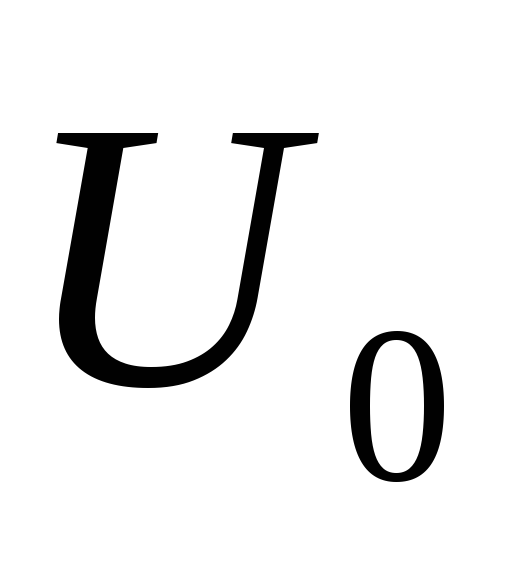 ,
а также от вида аппроксимации ВАХ
нелинейного элемента.
,
а также от вида аппроксимации ВАХ
нелинейного элемента.
12 Свойство нелинейной цепи изменять спектр выходного сигнала очень ярко проявляется, если входной сигнал представляет собой сумму гармонических колебаний с разными частотами. Спектр входного бигармонического сигнала представлен на рис.4.5.

В системах связи бигармонический сигнал получается, когда взаимодействуют два генератора (например, генератор входного сигнала и специальный генератор с фиксированной или перестраиваемой частотой).
Пусть ВАХ нелинейного двухполюсника описывается полиномом второй степени:
![]() (4.13)
Тогда напряжение, приложенное к входу,
помимо постоянной составляющей, содержит
два гармонических колебания с различными
частотами
(4.13)
Тогда напряжение, приложенное к входу,
помимо постоянной составляющей, содержит
два гармонических колебания с различными
частотами
![]() ,
,
![]() и амплитудами
и амплитудами
![]() ,
,
![]() .
.
![]() (4.14)
(4.14)
Сигнал (4.14) называется бигармоническим. Подставив (4.14) в (4.13) будем иметь:
![]()
![]() (4.15)
(4.15)
Учитывая
что,
![]() ,
а
,
а
![]() ,
получим:
,
получим:
![]()
![]() (4.16)
(4.16)
Спектральная диаграмма выражения (4.16) показана на рис.4.6.
