dsd1-10 / dsd-01=Компоненты ИС / Staroselskiy OLD / 03.bipolary / 9

109

9. Модель Гумеля-Пуна

9.1. Метод Гуммеля-Пуна

Транзисторный эффект состоит в переносе носителей, инжектированых через один из р-п переходов (Э-Б или К-Б), через базу до противоположного р-п перехода (К-Б или Э-Б).

В модели Эберса Молла этот эффект представлен отличными от нуля коэффициентами передачи тока (), которые являются феноменологическими параметрами модели.

В модели Гуммеля-Пуна транзисторный эффект представлен генератором сквозного тока неосновных носителей через базу, зависящим от напряжений на обоих р-п переходах. Для п-р-п транзистора сквозной ток выражается функцией

,

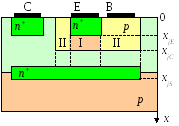
где — полный заряд основных носителей (дырок) в активной области базы (область I на рисунке).

Функция учитывает ряд эффектов, которые не могут быть учтены в модели Эберса –Мола.

Метод Гуммеля-Пуна состоит в решении уравнения непрерывности потока электронов через активную базу при следующих допущениях:

1) рекомбинация в базе незначительна, и в стационарном состоянии электронный ток в базе не зависит от координаты х;

2) коэффициент диффузии электронов в базе D_n не зависит от координаты х;

3) дырочный ток в активной базе мал: .

Эти допущения в реальных транзисторах выполнены с высокой точностью.

При допущении 1 сквозной ток

(9.1.1)

не зависит от х (знак «-» — положительное направление тока I_n противоположно оси х).

Напряженность электрического поля найдем из условия (допущение 3):

; . (9.1.2)

Подстановка (9.1.2) в (9.1.1) дает:

.

Умножив это уравнение на eS_E, получим:

.

Это уравнение проинтегрируем по всей базе (от х = х₁ до х = х₂; согласно принятым допущениям I_n и D_n не зависят от х:

.

В левой части в скобках — полный заряд дырок в базе .

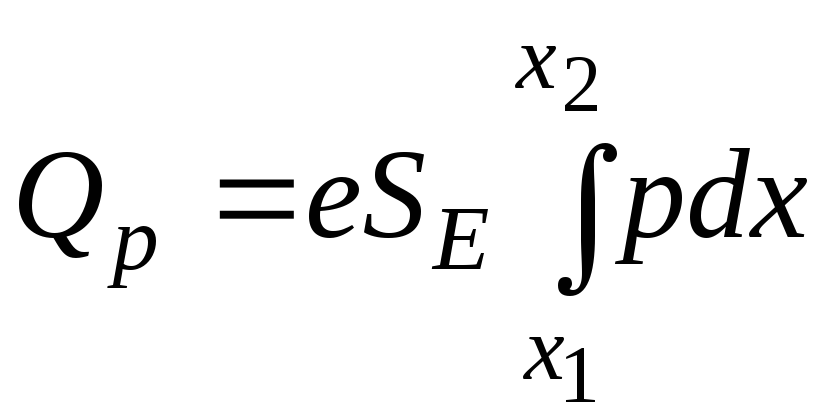В правой части: ; (9.1.3а) (9.1.3б)

(граничные условия). Таким образом:

.

.

Это соотношение можно представить в виде:

, (9.1.4)

где (9.1.5а) (9.1.5б)

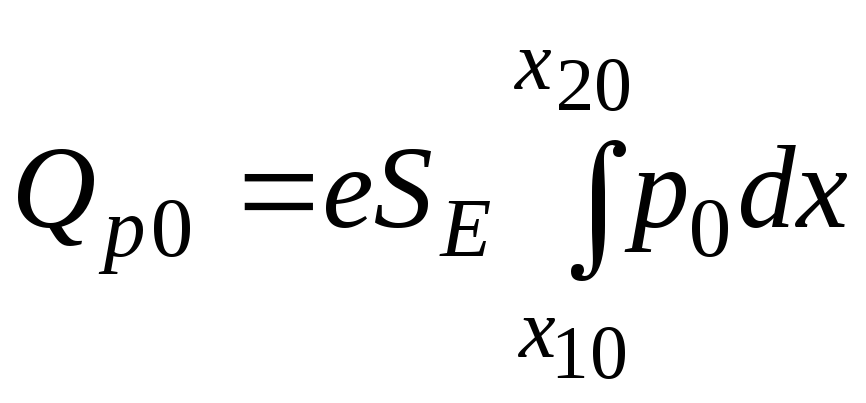, или 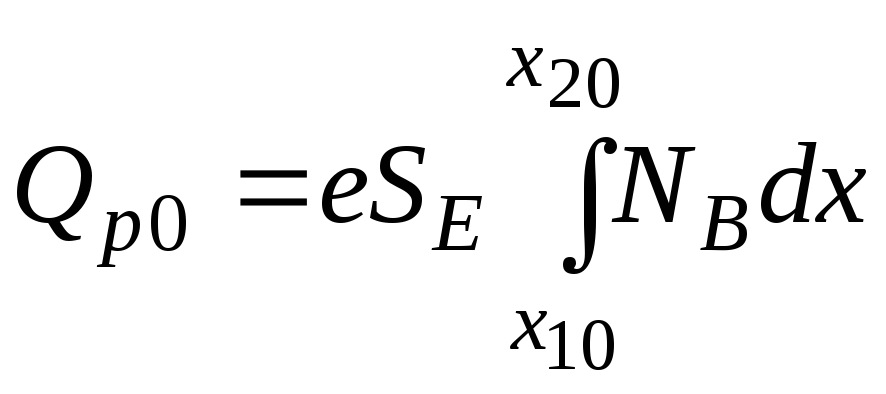— (9.1.6)

равновесный заряд дырок в базе (при ),

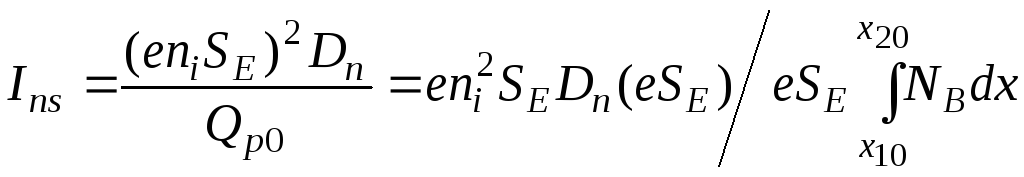
, или

— электронный тепловой ток эмиттерного перехода,

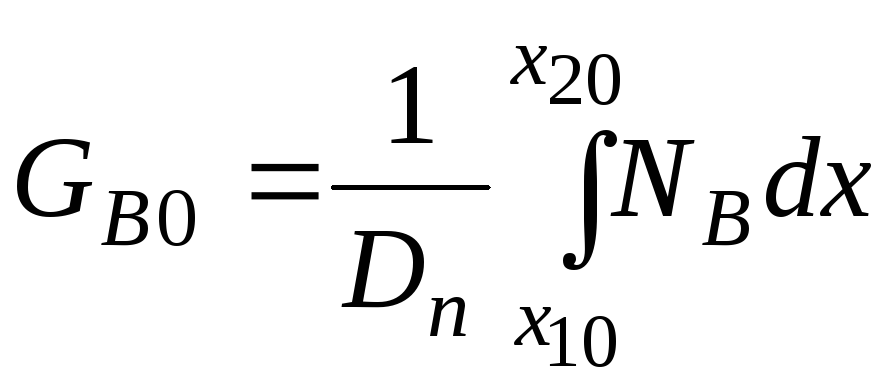— число Гуммеля в базе (как в идеальной модели).

Заряд должен быть определен в виде функции .

;

 

  

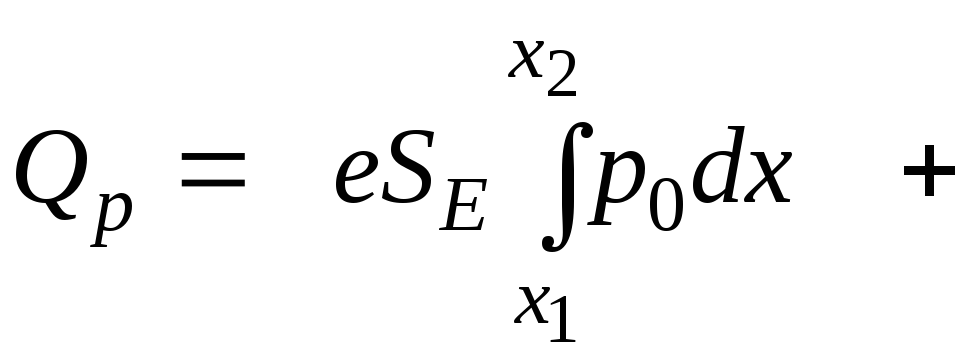
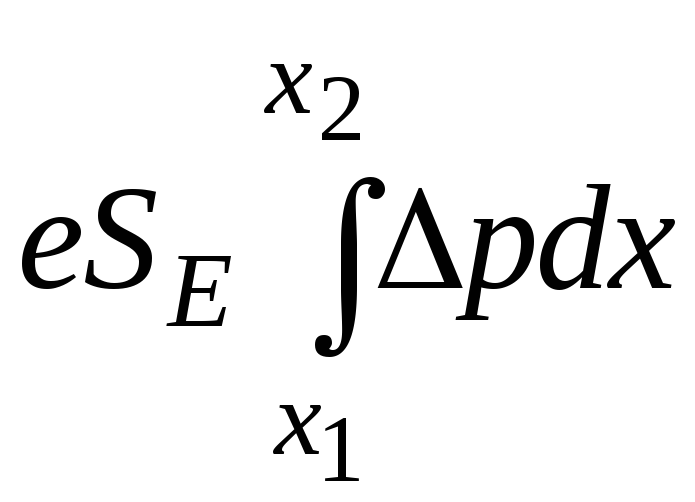
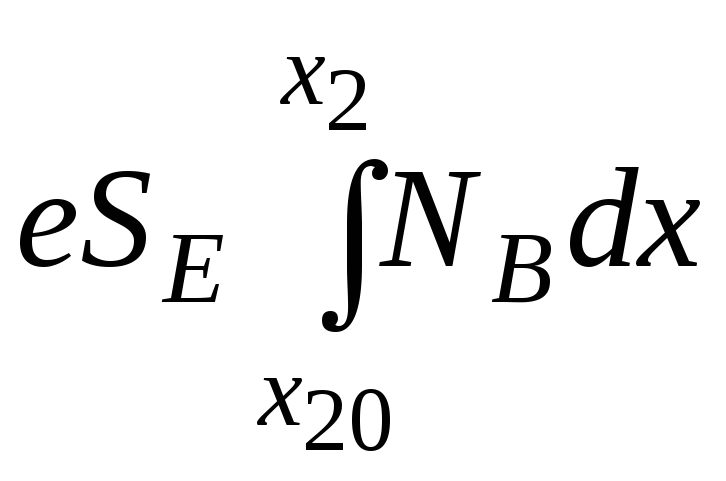
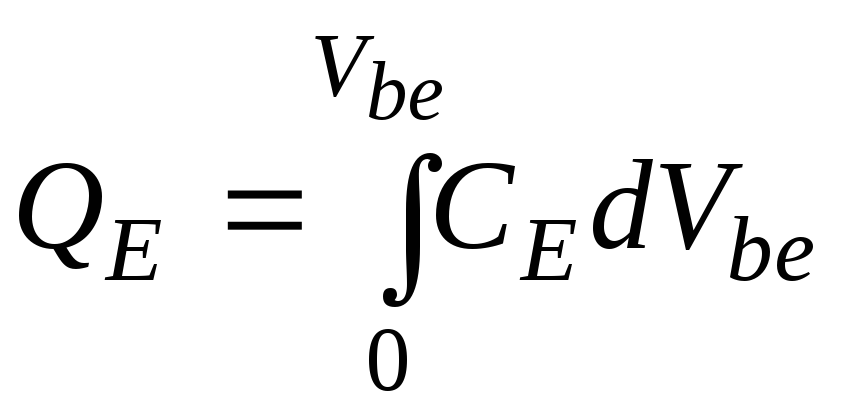
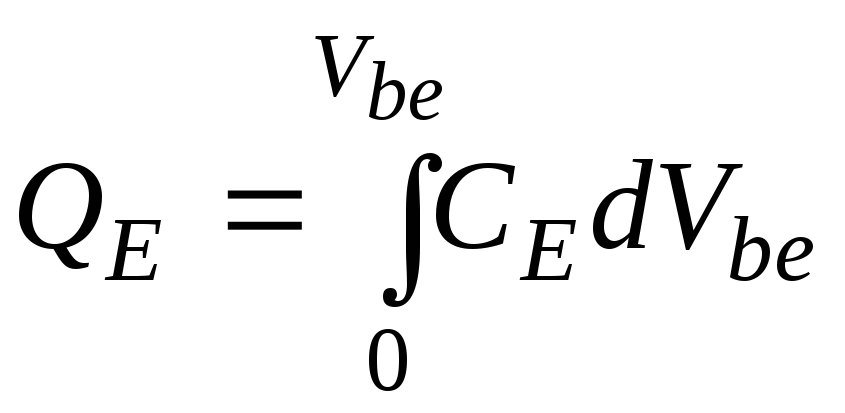
заряд в барьерной емкости

эмиттерного

перехода

заряд в барьерной емкости

коллекторного

перехода

. (9.1.7)

Подставляя (9.1.5а,б) в (9.1.7) и решая полученное уравнение относительно , находим:

; (9.1.8)

где согласно (9.1.5а,б)

(5б)

В этих уравнениях использованы параметры: , , и , а также функции и , определяющие и .

9.2. Эквивалентная схема Гуммеля-Пуна

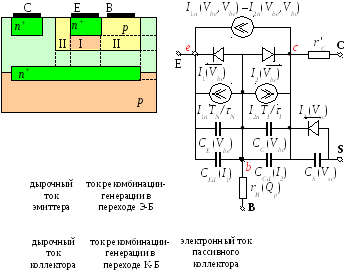
I_1nT_N /_N, I_2nT_I /_I —

токи рекомбинаци в активной базе I.

;

;

Функции I₁(V_be), I₂(V_bc) учитывают реальные ВАХ всех токов, кроме сквозного электронного тока.

9.3. Возможности модели Гуммеля-Пуна

Модель учитывает:

1). Произвольный уровень инжекции в активной базе — граничные условия (3а) и (3б).

2). Эффект Эрли — зависимости .

3). Изменение сопротивления активной базы при повышении уровня инжекции — r_B (Q_p).

Недостатки модели:

1). Сложность и отсутствие наглядности. Применяется только при численном (компьютерном) моделировании.

2). Модель не учитывает эффект оттеснения эмиттерного тока.