MATLAB задания 2сем / Задание для МП_11,17,П_12 / Практ_2_2_Ж
.docxПрактикум 2. Приложения определенного интеграла
|
Вычисление площадей |
|
Вычисление длины дуги и объёма тела вращения. |
1. Вычисление площадей фигур, ограниченных кривыми, заданными уравнениями в декартовых координатах.
Если интегрируемая на отрезке
функция
неотрицательна на нем, то криволинейная
трапеция, ограниченная прямыми
и графиком функции
имеет площадь, равную
Упражнение 1. Построить график
функции
на отрезке
Вычислить площадь фигуры, ограниченной
графиком функции и линиями
Если фигура ограничена кривыми
и
пересекающимися в точках
и
при
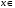
то
ее площадь равна
(можно считать, что она ограничена еще
и прямыми
).
Указание к упр1.
Для того чтобы увидеть как вообще ведет
себя данная функция
,
постройте несколько графиков в различных
диапазонах x=[-10*pi:0.01:10*pi]; x=[0:0.01:pi/2]; а для
большей наглядности постройте этот
график вместе с графиками функций
.
Не забудьте оформить график: hold on, grid
on, axis equal, введите и пометьте оси координат,
сделайте заголовок. На втором графике
выделите также линию
.
Упражнение 2. Построить графики
функций
и
Найти точки пересечения графиков.
Вычислить площадь фигуры, ограниченной
графиками.
Указание к упр1. Сделать рисунок.
2. Вычисление площади фигуры, ограниченной кривой, заданной параметрически .
Если плоская фигура ограничена прямыми
(
),
и графиком функции, заданной параметрическими
уравнениями
и функция
неотрицательна на отрезке
то площадь фигуры вычисляется по формуле
Для построения графика функции, заданной
параметрически нужно задать изменение
параметра
и функции
Пример 1.
t=0:pi/100:2*pi;
x=cos(t)+1;
y=sin(t);
plot(x,y)
Указание к прим.1.
Прежде, чем строить график из примера
1, попробуйте избавиться от параметра
и, перейдя в декартовую систему координат,
докажите, что это будет уравнение
окружности. Укажите радиус и центр
окружности.( При построении важно учесть
axis equal.)
Упражнение 3. Построить графики функций. Вычислить площадь фигуры, ограниченной графиками. Проверить без использования MatLab:
а)
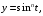при
Указание к упр.3 а). Докажите, что при n=1, это будет окружность радиуса 1, с центром в н.к.
б)
Указание к упр.3 б). Докажите, что это эллипс. Какие у него будут полуоси? Поместите его в соответствующий прямоугольник.
3. Вычисление площади фигуры, ограниченной кривой, заданной уравнением в полярных координатах.
Если фигура на плоскости ограничена
двумя лучами, выходящим из начала
координат
и
и кривой, заданной в полярных координатах
интегрируемой на отрезке функцией
то эта фигура имеет площадь, равную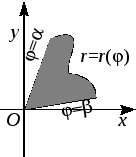 
Построение графика функции, заданной в полярных координатах можно свести к построению графика параметрически заданной функции.
Пример 1. Построить график функции
заданной в полярных координатах.
>> t=0:pi/100:2*pi;
>> r=t;
>> x=r.*cos(t);
>> y=r.*sin(t);
>> plot(x,y)
Упражнение 4.
а) Построить фигуру, ограниченную
графиком логарифмической спирали
и прямыми
Найти площадь фигуры.
б) Построить
фигуру, ограниченную кривыми
,
и
лучами
.
Прокомментируйте, что это будут за
фигуры. Найти площадь фигуры.
4. Вычисление длины дуги.
Если дуга кривой задана явным образом
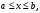где
-
непрерывно дифференцируемая на отрезке
функция, то ее длина вычисляется по
формуле
.
Упражнение 5. Найти длину дуги
параболы
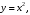от точки
до точки
Построить график функции, отметить
на графике точки.
Если дуга кривой задана параметрическими
уравнениями
где функции
и
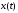- непрерывно дифференцируемые на отрезке
и
и
не обращаются одновременно в
(т.е.
при всех
),
то длина дуги вычисляется по формуле
.
Упражнение 6. Найти длину замкнутой
кривой, заданной параметрическими
уравнениями
Сделать рисунок.
Если дуга кривой задана в полярных
координатах уравнением
где функция
непрерывно дифференцируема на отрезке
то длина дуги вычисляется по формуле
Упражнение 7. Вычислить длину
замкнутой кривой, задаваемой уравнением
Сделать
рисунок.
5. Вычисление объема тела вращения.
Объем тела, образованного вращением
вокруг оси
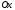криволинейной трапеции, ограниченной
прямыми
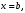
и графиком неотрицательной непрерывной
на отрезке
функции
равен
Объем тела, образованного вращением
вокруг оси
криволинейной трапеции, ограниченной
прямыми
и графиком неотрицательной непрерывной
на отрезке
функции
равен
(Формулы нужно уметь выводить)
Упражнение 8. Вычислить объем тела,
полученного при вращении криволинейной
трапеции, ограниченной графиком функции
и прямой
(
):
а) относительно оси
б) относительно оси
Указание к упр.8. В прошлом семестре на «линейной алгебре в среде МАТЛАБ» вы должны были строит анимацию с вращением,
Ищите на methodic\ВМ1\Линейная алгебра\МАТЛАБ_ЛА\МАТЛАБ ЖАРКОВА\модуль 3\Анимация
Попробуйте здесь сделать тоже самое.
Привожу КОД из соответствующего практикума:
figure;
grid on, hold on, box on, axis equal
view(19,7)
% Задаем оси координат с помощью прямой в параметрическом виде
t=[-5 5]; M=[0;0;0]; V=[1;0;0];
XYZ=M*ones(size(t))+V*t;
Lx=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:),'Color','black','LineWidth',2);
plot3(XYZ(1,2),XYZ(2,2),XYZ(3,2),'>k','MarkerSize',8,'LineWidth',4);
t=[-5 5]; M=[0;0;0]; V=[0;0;1];
XYZ=M*ones(size(t))+V*t;
t=[-5 5]; M=[0;0;0]; V=[0;1;0];
XYZ=M*ones(size(t))+V*t;
Ly=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:),'Color','black','LineWidth',2);
plot3(XYZ(1,2),XYZ(2,2),XYZ(3,2),'>k','MarkerSize',8,'LineWidth',4);
Lz=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:),'Color','black','LineWidth',2);
plot3(XYZ(1,2),XYZ(2,2),XYZ(3,2),'>k','MarkerSize',8,'LineWidth',4);
% Для оси вращения:
t=[-5 5]; M=[0;0;0]; V=[1;1;0];
XYZ=M*ones(size(t))+V*t;
L_os=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:),'Color','red','LineWidth',2);
% фигура вращения
plot3(XYZ(1,2),XYZ(2,2),XYZ(3,2),'>r','MarkerSize',8,'LineWidth',4);
M=[0;0;0]; V=[1;1;1];
XYZ=M*ones(size(t))+V*t;
L=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:));
% для анимации
for i=10:10:360, L=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:));rotate(L,[1 1 0],10+i,[1 1 0]),pause(0.5),end
Здесь фигура L (прямая) вращается вокруг оси L_os, а у вас функция должна вращаться вокруг одной из координатных осей.
У меня получилось. В следующий раз выложу скрипты, пока попробуйте сами сделать.