Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lab3_m4_vm1_vt_ppavsm_230100_62

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.04 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

и от неизвестных z1, z2 , z3 форма f примет уже канонический вид

f	z , z , z				4z2				z2	z2	(4)
		1	2 3			1			2	2 .	(4)
Разрешим равенства (3) относительно x1, x2 , x3 :
x y				y2			y3	,
x y								,
	1		1		2	2
					2	2

x2				y2 ,
x							y .
	3					3

Последовательное выполнение линейных преобразований X Q1Y и Y Q2Z , где

	1 1/ 2			1/ 2		1		0	0

Q1		0	1	0	Q2		0	1	1
		0	0	1			0	1
		0	0	1	,		0	1	1
					,

имеет матрицей
	1 1/ 2			1/ 2 1 0			1	1		0	2
R Q1Q2
R Q1Q2		0	1	0	0	1	1		0 1		1 .
		0	0	1	0	1			0	1	1
		0	0	1	0	1	1		0	1	1	.
												.

Линейное преобразование неизвестных

каноническому виду (4). Переменные

z1, z2 , z3 соотношениями

x	z			2z ,
1	1			3
x2		z2 z3 ,
x		z	2	z .
3			2	3

X RZ приводит квадратичную форму f к x1, x2 , x3 связаны с новыми переменными

Определение: Нормальным видом квадратичной формы называется сумма квадратов неизвестных с коэффициентами « 1» или « 1».

Определение:		Квадратичная	форма	f (x1,..., xn ) называется положительно
определённой,		если f (x1,..., xn ) 0		при всех	x1, , xn , за	исключением
x1	xn 0.	Квадратичная	форма	f (x1,..., xn )	называется	отрицательно

определённой, если f (x1,..., xn ) 0

при всех (x1,

, xn ) (0,

,0).

Теорема: Квадратичная форма

f x1,...,xn является положительно определённой

тогда и только тогда,

когда

приводится к нормальному виду,

содержащему n

квадратов

неизвестных с

коэффициентами

«+1»:

f (y ,..., y ) y2

... y2.

Квадратичная форма

f x1,...,xn

является отрицательно определённой тогда и

только тогда, когда f

приводится к виду

f (y ,..., y ) y2

... y2.

Определение: Пусть f X T AX

–

квадратичная

форма

с матрицей

i, j 1,...,n .

Миноры

a11

a12

a11

a12

a13

…,

a21

a22

a31

a32

a33

a11 ... a1n

... ...

...

называются угловыми минорами квадратичной формы

f .

an1 ...

ann

2.2. Критерий Сильвестра.

Теорема (Критерий Сильвестра): Квадратичная форма f x1,...,xn является

положительно определённой тогда и только тогда, когда все её угловые миноры строго положительны: 1, 2 , , n 0. Квадратичная форма f x1,...,xn

является отрицательно определённой тогда и только тогда, когда её угловые

миноры удовлетворяют неравенствам: 1 0, 2 0, 3 0,	4 0 и т.д.
Определение: Будем называть линейное преобразование	переменных Y CX
ортогональным, если матрица C ортогональная, т.е. CT C 1.

Сформулируем алгоритм приведения квадратичной формы к каноническому виду ортогональным преобразованием:

1.Находим собственные значения линейного оператора, решая характеристическое уравнение det(A E) 0.

2.Для каждого собственного значения находим собственные векторы, решая систему линейных уравнений (A E)x 0. (У этой системы мы должны найти

фундаментальную систему решений).

3.Если собственное значение имеет кратность, большую 1 (в

характеристическом уравнении), то векторы из ф.с.р. могут оказаться не ортогональными друг другу – в этом случае к ним надо применить процесс

ортогонализации Шмидта (изучите самостоятельно, читайте:

Ржавинская Е. В., Олейник Т. А., Соколова Т. В. Лекции по линейной алгебре и аналитической геометрии, М., МИЭТ. 2007. )

4.Нормируем найденные собственные векторы, т.е. каждый вектор делим на его длину.

5.Записываем канонический вид квадратичной формы и преобразование координат, приводящее её к этому виду.

Пример: Привести данную квадратичную форму к каноническому виду

ортогональным преобразованием координат:

f (x1, x2 , xn ) 3x12 3x22 3x32 2x1x2 2x1x3 2x2x3.

Решение: Составим матрицу этой квадратичной формы:

3		1	1
A	1	3	1 .

	1	1
	1	1	3
Составим характеристическое уравнение:

	3	1	1
	3	1	1
	1	3	1	0.
	1	1	3
Отсюда получаем:				( 4)2 ( 1) 0.	Корни характеристического уравнения:	4,
					1,2
3 1.

Для 4 система уравнений, из которой находятся собственные векторы,

выглядит так:

x1 x2 x3 0,
		x2	x3 0,
x1
	x	x	x 0.

	1	2	3
Её фундаментальная система решений: u1 ( 1, 0,1),				u2 ( 1,1, 0). Эти векторы не

ортогональны друг другу, поэтому применим к ним процесс ортогонализации

Шмидта. Положим v1 u1,						v2 u2		v1	и подберём		так,	чтобы было выполнено
условие	v	v .	Имеем:				v v 0,		т.е.	(u	v )v	0,	u2v1	1 .
	2	1					2	1		2	1 1		v2	2
													1
Следовательно, v			u	1 v			1 ( 1, 2, 1).
		2	2	2	1		2

Запишем теперь систему уравнений для 1:

2x1 x2 x3 0,
		2x2 x3 0,
x1
	x	x	2x 0.

	1	2	3

Её ф.с.р. состоит из одного вектора: u3 (1,1,1). Этот вектор ортогонален векторам v1

и v2.

		Пронормируем векторы v1, v2 , u3 , разделив каждый вектор на его длину.
Получим ортонормированный базис из собственных векторов: e										1	( 1, 0,1),
Получим ортонормированный базис из собственных векторов: e											( 1, 0,1),
								1	2
									2
e	1		( 1, 2, 1),	e		1	(1,1,1).
e			( 1, 2, 1),	e			(1,1,1).
2	6			3		3
	6					3
		Матрица перехода от исходного базиса e1 (1, 0, 0),						e2 (0,1, 0),	e3 (0, 0,1) к
новому базису e , e , e						равна:
	1			2	3

	1	1		1

	2	6		3
	2	6		3
		2		1
S	0				.

		6		3
		6		3
	1		1	1

	2	6		3
	2	6		3

В новых

координатах

квадратичная форма будет иметь вид f 4x 2

Старые координаты выражаются через новые следующим образом:

1/ 6

2 / 6

1/ 3

1/ 6

1/ 2

1/ 3

Обратные формулы:

4x 2 x 2.

2 3

1/ 6 2 / 6

1/ 3 1/ 3

1/ 3

т.е.

1				( x			x ),
				( x			x ),
2			1				3
2
1				( x 2x			x ),
				( x 2x			x ),
6			1		2		3
6
	1	( x x				x ).
		( x x				x ).
3			1		2		3
3

2.3. Применение теории квадратичных форм к кривым и поверхностям второго порядка

Пусть на плоскости задана декартова система координат (декартов базис i , j

и точка О – начало координат). Рассмотрим общее уравнение второго порядка:

a x2	2a	xy a	y2 2a x 2a y a 0.		(5)
11	12	22	1	2

Обозначим через f (x, y) сумму старших слагаемых:

f(x, y) a11x2 2a12xy a22 y2

ирассмотрим квадратичную форму f (x1, x2 ) a11x12 2a12x1x2 a22x22 . Её матрица

a11	a12	симметрическая.
Q	a	симметрическая.
a	a
21	22

В общем случае преобразование поворота осей координат


	x	x cos		y sin
y x sin y cos ,												(6)
приведёт линию (5) к виду
x 2		y 2	2b x 2b y b 0					.				(7)
1		2		1	2			.				(7)
							a12			a11	a12
Обозначим ( )						a11	a12		, (0)	a11	a12	.
						a	a			a	a
						21	22			21	22

b b12 b22 c,1 2

и c разных знаков

эллипс

кривая эллиптического типа

и c одного знака

мнимый эллипс

c 0

точка

c 0

гипербола

кривая гиперболического типа

c 0

пара пересекающихся

прямых

пара мнимых

и c одного знака

параллельных прямых

b1 0

пара параллельных

кривая

и c разных знаков

прямых

параболического

c 0

пара совпадающих

типа

прямых

b1 0

парабола

Пример: Определить вид и расположение кривой второго порядка

f (x, y) 5x2 4xy 2y2 2 5x 8 5y 1 0

(8)

Решение. Слагаемые второго порядка в (8) составляют квадратичную форму

4xy 2y2

f (x, y) 5x2

которую преобразование неизвестных по формулам

y ,

(9)

приводит к сумме квадратов									f (x , y ) 6x 2 y 2
приводит к сумме квадратов
Тогда уравнение кривой (8) преобразованием (9) приведётся к виду
	2		2		2		1				1		2
	2		2		2		1				1		2
6x		y		2 5		x		y		8 5		x		y	1 0
6x		y		2 5		x		y		8 5		x		y	1 0
					5		5				5		5		.
															.
Здесь 1			6, 2		1 и, следовательно, 6 0 , – кривая эллиптического типа.

Как при рассмотрении выше случая 1, соберём слагаемые, содержащие неизвестное x и дополним их до полного квадрата, аналогично поступим со слагаемыми,

содержащими y :

6 x 2 2x 1 6 y 2 14y 49 49 1 0

, или

6 x

1 y 7 54.

x 1

Полагаем

y y 7

и получим

a 3,b 3

Это

уравнение

эллипса

с полуосями

центром в точке O ( 1, 7)

y"	y'	y
y"	y'
			x'
			arctg1/2
		O(O')	x

Рис. 14.1

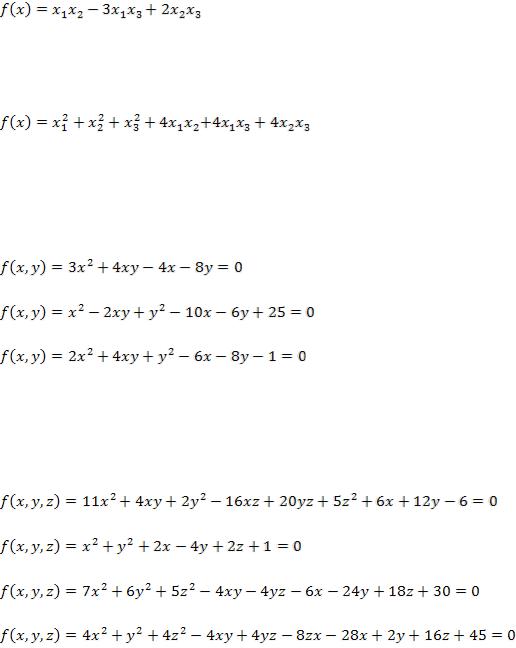
2.4. Задания

Задание 2.1. Определить, является ли положительно определённой квадратичная

форма f x1, x2 , x3 x12 2x22 x32 2x1x2 4x1x3 2x2 x3 .

Задание 2.2. Методом Лагранжа привести форму к каноническому виду:

Задание 2.3. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду

Задание 2.4. Записать каноническое уравнение кривой второго порядка, определить тип и найти каноническую систему координат. Применить теорию квадратичных

форм.

Задание 2.4. Записать каноническое уравнение поверхности второго порядка, определить тип и найти каноническую систему координат. Применить теорию

квадратичных форм.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в папке Модуль 4

#
05.06.2015262 б15GaussMethod.asv
#
05.06.2015317 б16GaussMethod.m
#
05.06.2015749.15 Кб18lab1_m4_vm1_vt_ppavsm_230100_62.pdf
#
05.06.2015632.75 Кб16lab2_m4_vm1_vt_ppavsm_230100_62.pdf
#
05.06.20151.46 Mб18lab3_m4_vm1_vt_ppavsm_230100_62.doc
#
05.06.20151.04 Mб18lab3_m4_vm1_vt_ppavsm_230100_62.pdf
#
05.06.2015284 б14matrix_multiply.m
#
05.06.2015151 б14print_hello.m
#
05.06.2015287 б14Untitled.asv
#
05.06.2015318 б14Untitled.m
#
05.06.2015581 б14Untitled1.asv