1 семестр_1 / МА / Практ_12_0

Практикум 12. Интегрирование

Нахождение неопределённых и определённых интегралов

1. Неопределённые интегралы.

Неопределённый интеграл функции находится с помощью функции int(F, v), где F – символическое выражение под интегралом, v – переменная, по которой берётся интеграл (по умолчанию определяется с помощью вызова symvar(F), а если F – константа, то v – символическая x).

Пример 1. Найдём :

>> syms x a b

>> int(sin(a*x)*cos(b*x), x) %% или int(sin(a*x)*cos(b*x)), так как x – переменная по умолчанию в этом выражении

ans =

-(b*sin(a*x)*sin(b*x) + a*cos(a*x)*cos(b*x))/(a^2 - b^2)

То есть Заметьте, что Matlab не добавляет константы в конце.

Пример 2. Найдём

>> syms x n

>> int(x^n, x)

ans =

piecewise([n = -1, log(x)], [n <> -1, x^(n + 1)/(n + 1)])

Это означает 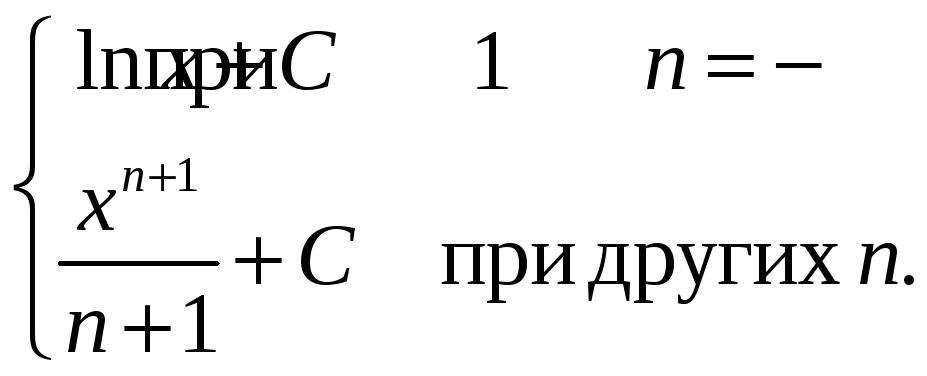Что не так в этом ответе?

Если Matlab не может найти интеграл, то сообщает об ошибке и возвращает ненайденный интеграл.

Пример 3. Попробуем вычислить

>> int(acos(sin(x)), x)

Warning: Explicit integral could not be found.

ans =

int(acos(sin(x)), x)

Упражнение 1. Найдите: a) б) в) и запишите полученные результаты в математических обозначениях.

2. Символическое вычисление определённых интегралов

Определённый интеграл -- это площадь фигуры, ограниченной графиком функции на отрезке осью и прямыми и Если известен то определённый интеграл можно вычислить по формуле Ньютона-Лейбница:

Функцию int можно также использовать для вычисления определённых интегралов, передав ещё два аргумента – a и b. Это могут быть числа или символические выражения.

Пример 4.

>> syms x

>> int(x^2,0,1)

ans =

1/3

Пример 5. Matlab вычислить так же не может, как и в примере 3:

>> syms x pi; int(acos(sin(x)), x, 0, pi)

Warning: Explicit integral could not be found.

ans =

int(acos(sin(x)), x = 0..pi)

Но можно вычислить его приближение с помощью знакомых нам функций double и vpa (с помощью способов, описанных в следующем параграфе):

>> vpa(int(acos(sin(x)), x, 0, pi), 10)

Warning: Explicit integral could not be found.

ans =

2.4674011

3. Численное вычисление интегралов

Часто для разных целей приходится считать интегралы функций, которые или нельзя взять аналитически , или неизвестно, как это сделать. В таких случаях формула Ньютона-Лейбница бесполезна, и применяется один из способов численного интегрирования, различающихся сложностью, скоростью работы, и точностью результатов. Два из них реализованы библиотечными функциями Matlab: trapz использует метод трапеций, а quad – формулу Симпсона (или метод парабол). На практике их применение различается примерно так же, как plot и fplot – trapz(X,Y) принимает вектор аргументов X и вектор соответствующих значений функции Y, а quad(f, a, b, tol) – ссылку на функцию f, пределы интегрирования a и b, и точность приближения tol (по умолчанию

Пример 6. Точное значение Посчитаем приближённо с помощью функции trapz:

>> X = 0:pi/10:pi;

>> Y = sin(X);

>> trapz(X,Y)

ans =

1.9835

И с помощью quad:

>> quad(@sin,0,pi,1e-6)

ans =

2.0000

Может показаться, что ответ точный, но это не так:

>> format long

>> ans

ans =

1.999999996398431

Упражнение 2. Найдите точные (если возможно) значения и приближённые (с помощью trapz и quad) значения интегралов а) б) в*)

3