Статьи на перевод PVDF_P(VDF-TrFE) / Tuned dielectric, pyroelectric and piezoelectric properties of ferroelectric P(VDF-TrFE) thin films using mechanical loads

I. INTRODUCTION

Polyvinylidene fluoride (PVDF) and its copolymers with trifluoroethylene (TrFE) exhibiting paraelectric to ferroelectric transition, like the traditional perovskite-type ferroelectric materials, have become the subject of much scientific and technological research, because of large energy density, promising thermoelectric, and giant electromechanical properties. P(VDF-TrFE) exhibits high piezoelectric response, which determines its wide application in piezoelectric transducers and sensors.1,2 A large electrocaloric effect is reported in P(VDF-TrFE) at temperatures near and above the ferroelectric-paraelectric transition.3 A relatively high value of the spontaneous polarization leads to consideration of P(VDF-TrFE) for all-organic memory and mass data storage devices.4–7

It is well-known that the properties of ferroelectrics are highly sensitive to the mechanical loads, such as external applied stresses and strains.8–10 In ferroelectrics, mechanical loads can change the weak balance between long-range dipole-dipole electrostatic interactions and short-range repulsive forces. Their subtle competitions are known as the origin of ferroelectric instability.11 Therefore, both Curie temperature and polarization state will be sensitively depended on the external mechanical loads. The strong stress-polarization coupling is responsible for a number of interesting physical properties in ferroelectric materials. Although a Landau-Ginzburg-Devonshire phenomenological model has been successfully used to investigate the effect of misfit strains and external stresses on the properties of pervoskite-type ferroelectric thin films,12–14 there

a)Author to whom correspondence should be addressed. Electronic mail: liuzg@nju.edu.cn.

were rarely used for studying ferroelectric polymers. There is a real need for a mutual understanding of the properties of ferroelectric polymer thin films, which is necessary to satisfy their applications with improved design. Ducharme et al.15 used Landau theory to calculate the intrinsic coercive field of P(VDF-TrFE). Liu et al.16 used the LandauDevonshire phenomenological model to study the effect of in-plane misfit strain on dielectric and pyroelectric properties of P(VDF-TrFE) thin films. Li et al.17 investigated the thickness effect of ferroelectric polymer thin film by using the three-dimensional phase field method. However, considering the effect of external mechanical load on ferroelectric polymer thin films has not been referred to in theory. Furthermore, the external mechanical load may induce the change of other properties and open more opportunities for applications. In this paper, we present an investigation of the phase transition and physical properties of ferroelectric copolymer P(VDF-TrFE) 65:35 films under external mechanical load calculated by using Landau theory.

II. LANDAU THEORY

For a film/substrate system subjected to external stress (displayed in Fig. 1), the stress r3 in a single-domain film is governed by the applied load and the shear stressesr4 and r5will be neglected (r4 ¼ r5 ¼ 0). Considering the in-plane strains arising from lattice mismatch between the film and the substrate and the external mechanical force, the elastic Gibbs free energy is not appropriate for the description of the films. In this work, we assume that in-plane strains are isotropy, namely u1 ¼ u2 ¼ um, and the shear strain u6 ¼ 0. Because the polarization is assumed along the film normal, the standard elastic free energy G can be written as

FIG. 1. Schematic of P(VDF-TrFE) thin film with applied (a) compressive stresses (r3 < 0) and (b) tensile stresses (r3 > 0).

Here a, b, and c are the dielectric stiffness coefficients, s11 and s12 are the elastic compliances at constant polarization, and Q11 and Q12 are the electrostrictive constants. The dielectric stiffness ashould be given by a linear temperature dependence a ¼ a0ðT T0Þ based on the Curie-Weiss law, where T0 is the Curie–Weiss temperature.

the film are @G=@r1 ¼ @G=@r2 ¼ um, @G=@r6 ¼ 0, and @G=@r3 ¼ u3. Solving for the in-plane stresses, one finds

that r6 ¼ 0, and r1 ¼ r2 ¼ ðum Q12P2Þ=s11 þ s12. So the modified thermodynamic potential can be written as

One can express the out-of-plane strain u3 through its dependence on the out-of-plane polarization P, the external stress r3, and the in-plane strain um as

The Curie temperature Tc of the film refers to the paraelectric-ferroelectric transition at zero field. It varies with in-plane strains and applied external mechanical loads

III. RESULTS AND DISCUSSION

To focus on the effect of external mechanical loads, we only use the approximate effective in-plane strain of 0.02 for a thin P(VDF-TrFE) (65/35) film grown on a tensile substrate. The parameter values of coefficients for P(VDFTrFE) thin film are listed in Table I.18–20

In order to investigate the physical properties of P(VDFTrFE) thin films, firstly, the equilibrium states of the phases should be taken into account, which are obtained by minimiz-

ing the modified thermodynamic potential ~. To describe the

G

transformation of the thermodynamic equilibrium states occurring in films during external loads, it is useful to develop external stress-temperature the phase diagram, where the temperature T and external stress r3 are regarded as two independent variables, whereas the in-plane strain is assumed to be constant. Using Eq. (6), we calculated the phase diagram for the P(VDF-TrFE) thin films under the short-circuited condition (E ¼ 0). Figure 2 shows the external stress-temperature phase diagram under in-plane strains um ¼ 0.02. Whether external stress is tensile stress or compressive stress, b is always negative. So the mechanical load does not change the order of the paraelectric to ferroelectric phase transition, which remains of first-order in bulk materials. As can be seen, the phase transition temperature has a linear change with

TABLE I. Data for P(VDF-TrFE) copolymers.

aReference 18. bReference 19. cReference 20.

altering external mechanical loads. The ferroelectric transition temperature rises with increasing magnitude of compressive stress (r3 < 0), which is consistent with the experiment data in Ref. 21, and decreases with increasing tensile stress (r3 > 0) due to Q11 ð2Q12s12=s11 þ s12Þ < 0. On the contrary, for perovskite-like ferroelectric films experiencing a second-order phase transition at Tc, the phase transition temperature decreases with increasing external compressive

stress and rises with increasing tensile stress due to Q11 ð2Q12s12=s11 þ s12Þ > 0.13 This difference is attributed to the different intrinsic parameters between pervoskite and

polymer ferroelectrics. Especially, the electrostrictive constants play an important role. For pervoskite-like ferroelectrics, Q11 > 0 and Q12 < 0 (in Refs. 12 and 14), while Q11 < 0 and Q12 > 0 (in Ref. 20) for polymer ferroelectrics. From Eq.

hydrostatic pressure phase diagram is also plotted in Fig. 2 (inset of Fig. 2). It is noticeable that Tc increases under hydrostatic pressure since the hydrostatic electrostrictive coefficient Qh ( ¼ Q11 þ 2Q12) is negative,20 which is in agreement with the experiment results.22 However, hydrostatic pressure leads to a decrease of Tc compared with the perovskite ferroelectrics since the sum (Q11 þ 2Q12) is positive.23

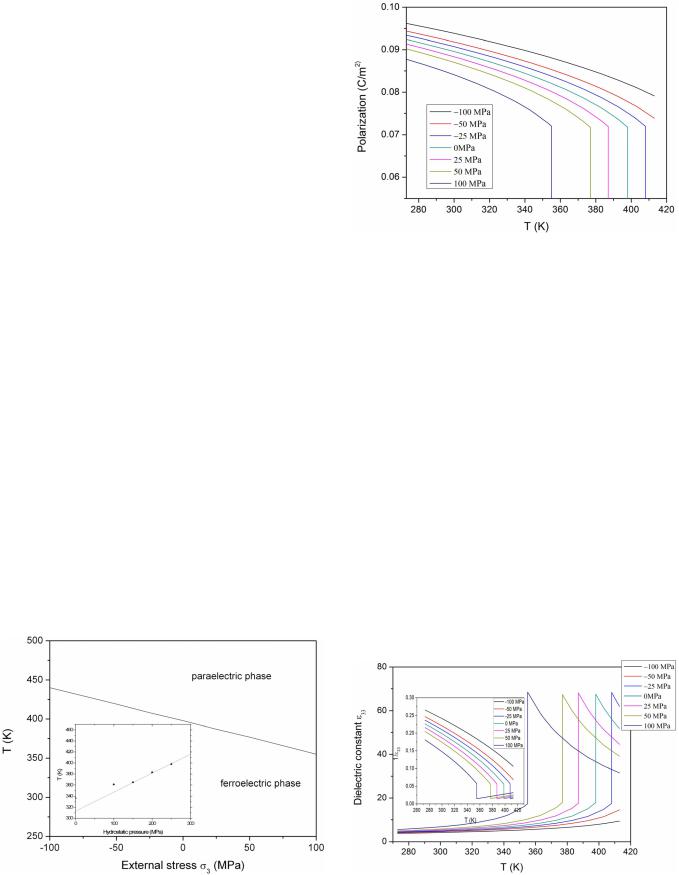
The temperature dependence of the out-of-plane polarization for P(VDF-TrFE) films under different applied external stresses can be shown in Fig. 3. Ferroelectric polarization in P(VDF-TrFE) arises from alignment of molecular dipoles in ferroelectric phase, which consists of all trans-(CH2 – CF2)x(CH2 – CHF)1 x-chains arranged in parallel rows in a quasihexagonal crystalline packing.1,15,24 External compressive stress increases the spontaneous out-of-plane polarization and tensile stress suppresses the polarization. The change of the out-of-plane polarization can produce a depolarization current, which could be measured when the mechanical load is applied to a film sandwiched between two electrodes. The out-of-plane polarization experiences a discontinuous variety at the phase transition temperature Tc, at which the phase

FIG. 3. (Color online) Temperature dependence of out-of-plane polarization for P(VDF-TrFE) thin film under different external stresses at um ¼ 0.02.

transformation is of first-order. However, for perovskite ferroelectrics, the film out-of-plane polarization gradually decreases with increasing compressive stress.13

Figure 4 shows the out-of-plane relative dielectric constant e33under different external mechanical loads. Although compressive stress increases the out-of-plane spontaneous polarization, it suppresses the out-of-plane relative dielectric constant e33 below Tc and increases e33 above Tc. In contrast, tensile stress raises e33 below Tc and reduces e33 above Tc. The out-of-plane relative dielectric constant e33 experiences a discontinuous jump at the phase transition temperature Tc due to the first-order phase transformation. The temperature dependence of the reciprocal dielectric constants under different stresses is also plotted in Fig. 4 (inset of Fig. 4). As clearly shown in the figure, the temperature variation changes from a negative dependence to a positive one at Tc, where the reciprocal dielectric constants are discontinuous because of the first-order phase transition. Above Tc, the temperature dependence of the reciprocal dielectric constants shows a linear relation fitting to the Curie-Weiss’s law. The reciprocal dielectric constants increase below Tc and decrease above Tc with the increase of compressive stress

FIG. 2. The external stress-temperature phase diagram of P(VDF-TrFE) thin film under in-plane misfit strain um ¼ 0.02. Inset displays the hydrostatic pressure-temperature phase diagram of P(VDF-TrFE) crystal (~ experiment data from Ref. 22).

FIG. 4. (Color online) Temperature dependence of out-of-plane dielectric constant for P(VDF-TrFE) thin film under different external stresses at um ¼ 0.02. Inset shows the temperature dependence of the reciprocal dielectric constants under different stresses at um ¼ 0.02.

FIG. 5. (Color online) Temperature dependence of pyroelectric coefficient for P(VDF-TrFE) thin film under different external stresses at um ¼ 0.02.

and vice versa. The calculated results are consistent with the experiment ones.21

We also investigated the out-of-plane pyroelectric response for applications in infrared sensors. Figure 5 shows the temperature dependence of the pyroelectric coefficient under different external mechanical loads. It is obvious that pyroelectric response reaches the maximum at the phase transition temperature and the external compressive stress moves the peak into the direction of high temperature. Furthermore the calculation shows that external compressive stress suppresses the out-of-plane pyroelectric response because of the increased out-of-plane spontaneous polarization.

Piezoelectricity is the basis for a large number of sensor and transducer applications. Figure 6 shows the temperature dependence of the out-of-plane piezoelectric response d33under different external stresses. The out-of-plane piezoelectric response d33 is negative due to Q11 ð2Q12s12=s11 þs12Þ < 0, which is consistent with the experiment results.25 Although external compressive stress increases the out-of- plane polarization and suppresses the out-of-plane relative dielectric constant, the total effect is that the external com-

FIG. 6. (Color online) Temperature dependence of piezoelectric coefficient for P(VDF-TrFE) thin film under different external stresses at um ¼ 0.02.

pressive stress decreases the absolute value of the out-of-plane piezoelectric response d33. In contrast, external tensile stress increases the absolute value of d33.

IV. CONCLUSIONS

In summary, the effect of external mechanical loads on the dielectric, pyroelectric, and piezoelectric responses of P(VDF-TrFE) thin films has been investigated by applying the phenomenological thermodynamic theory. The theoretical analysis indicates that phase transition temperature can be shifted by external mechanical loads. External compressive stress increases the phase transition temperature Tc and the out-of-plane polarization and suppresses the out-of-plane pyroelectric coefficient and piezoelectric coefficient (absolute value). Furthermore, compressive stress suppresses the out-of-plane relative dielectric constant e33 below Tc and increases e33 above Tc. This indicates the feasibility of design optimization by tuning the properties of ferroelectric polymer thin films using the mechanical load.

ACKNOWLEDGMENTS

This research was jointly supported by the National Key Project for Basic Research of China (2012CB619406), National Natural Science Foundation of China (Grant No. 11134004), and the Chinese National Key Project under Grant No. 2009ZX02023-5-4.

1A. J. Lovinger, Science 220, 1115 (1983).

2S. B. Lang, and S. Muensit, Appl. Phys. A 85, 125 (2006).

3B. Neese, B. C. Chu, S. G. Lu, Y. Wang, E. Furman, and Q. M. Zhang, Science 321, 821 (2008).

4Z, Hu, M. Tian, B. Nysten. and A. M. Jonas, Nature Mater. 8, 62 (2009). 5Y. J. Park, S. J. Kang, B. Lotz, M. Brinkmann, A. Thierry, K. J. Kim, and C. Park, Macromolecules 41, 8648 (2008).

6S. Ducharme and A. Gruverman, Nature Mater. 8, 9 (2009).

7K. El-Hami, M. Hara, H. Yamada, and K. Matsushige, Ann. Chim. Sci. Mat. 26, 217 (2001).

8K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. B. Chen, X. Q. Pan, V. Gopalan, L.-Q. Chen, D. G. Schlom, and C. B. Eom, Science 306, 1005 (2004).

9J. B. Neaton and K. M. Rabe, Appl. Phys. Lett. 82, 1586 (2003). 10Z. L. Wang and J. H. Song, Science 312, 242 (2006).

11W. Cochran, Adv. Phys. 9, 387 (1960).

12N. A. Pertsev, A. G. Zembilgotov, and A. K. Taganatsev, Phys. Rev. Lett. 80, 1988 (1998).

13A. Yu. Emelyanov, N. A. Pertsev, and A. L. Kholkin, Phys. Rev. B 66, 214108 (2002).

14G. Bai and W. H. Ma, Physica B 405, 1901 (2010).

15S. Ducharme, V. M. Fridkin, A. V. Bune, S. P. Palto, L. M. Blinov, N. N. Petukhova, and S. G. Yudin, Phys. Rev. Lett. 84, 175 (2000).

16P. F. Liu, X. J. Meng, J. H. Chu, G. Geneste, and B. Dkhil, J. Appl. Phys. 105, 114105 (2009).

17T. Li, C. Q. Chen, and J. X. Zhou, Theor. Appl. Mech. Lett. 1, 011008 (2011).

18T. Furukawa, Ferroelectrics 57, 63 (1984).

19H. Wang, Q. M. Zhang, L. E. Cross, and A. O. Sykes, J. Appl. Phys. 74, 3394 (1993).

20Z. Y. Cheng, T. B. Xu, V. Bharti, S. X. Wang, and Q. M. Zhang, Appl. Phys. Lett. 74, 1901 (1999).

21K. Matsushige, Phase Transitions 18, 247 (1989).

22S. Miyata, T. Itoh, Y. Saruyams, Y. Kawasaki, T. Yanagisawa, and R. Iwata, J. Phys. Soc. Jpn. 73, 1793 (2004).

23G. A. Rossetti, L. Eric Cross, and K. Kushida, Appl. Phys. Lett. 59, 2524 (1991).

24T. Furukawa, Phase Transitions 18, 143 (1989).

25K. Omote, H. Ohigashi, and K. Koga, J. Appl. Phys. 81, 2760 (1996).