Статьи на перевод PVDF_P(VDF-TrFE) / Fundamental formulations and recent achievements in piezoelectric

Review

energy storage components, and holds great promises for directly drawing energy from ambient mechanical resources, powering small electronics and achieving self-powered electronic devices. This distinct feature makes them attractive for a wide range of applications in nanoelectromechanical systems (NEMS), such as nanosensors/transducers, nanogenerators, nanoresonators, diodes, and piezoelectric eld-e ect transis-

An intriguing possibility is the utilization of work produced by the human body via daily activities.6–8

To date, these PNs have been synthesized in various con g- urations such as nanowires, nano lms, nanoplates, nanoribbons, and nanorings. Since Wang and Song's pioneering work9 on the rst nanogenerator prototype using piezoelectric nanowires for converting mechanical energy into electricity, there has been an increasing interest in investigating various technologies, including theoretical calculations and experimental characterization methods, to promote the development of self-powered PNs. To quote only a very few works in this direction, let us mention ref. 10–15.

The experimental work on PNs has been reported by many researchers, and the recent review of Xu and Wang16 should be mentioned. However, only the experimental progress that has been made within the context of on one-dimensional ZnO nanostructures was given in ref. 16.

With the advent of other building blocks of nanogenerators, lots of experimental characterization methods have been proposed recently. In addition, many fundamental theories about nanosized piezoelectric structures are raised to optimize the design of di erent PNs, and prompt the further development of new nanogenerators. To date, the theoretical work has mainly focused on the coupling surface/interface theory17,18 and the theory of nonlocal piezoelectricity.19 The coupling surface/ interface theory of stress and electric displacement plays an important role in the electromechanical energy conversion technologies. The theory of nonlocal piezoelectricity can provide a foundation for increasing the strength and electric potential of PNs.

Vijay Gupta is a Professor of Mechanical and Aerospace Engineering, Professor of Materials Science and Engineering, and Professor of Bioengineering at the University of California Los Angeles. He received a Bachelor of Technology degree in Civil Engineering from the Indian Institute of Technology (Bombay), a M.S. in Civil Engineering from the Massachusetts Institute of Technology and a Ph. D. in

Mechanical Engineering also from MIT. Professor Gupta's research covers biomechanics, impact management, surface science, applied mechanics, and composite materials. He has published over 200 publications with four U.S. Patents assigned. He is a Fellow of the ASME.

View Article Online

Nanoscale

Most recently, PNs have attracted more and more concerns not only in the research of nanoelectromechanical systems, but also in the fundamental theories in piezoelectric nanotechnology. To promote the further investigation of PNs, a systematic review of the fundamental development in recent years is demonstrated in this work, and some practical models and growth mechanisms of PNs will be reviewed, and the perspective of this novel technique will be discussed.

2 Types of PNs

Under external force, a deformation inside piezoelectric nanostructured materials will occur. Then, a piezoelectric potential can be generated on the side surfaces due to crystal lattice distortion. The electrical potential can be used to power nanodevices. Based on the dimensions of PNs, they are classi ed into the following four main types.

2.1Zero-dimensional (0D) PNs

Zero-dimensional piezoelectric nanomaterials are the foundation of many other types of PNs. They include nanocluster materials and nanodispersions, i.e., piezoelectric materials in which nanoparticles are isolated from each other, as shown in Fig. 1. Piezoelectric nanoparticles o en possess nonlinear optical, pyroelectric, magnetic, or ferroelectric properties. Only in recent years have zero-dimensional piezoelectric nanocomposites attracted more attention.

By introducing rough Al powders into an N2 thermal plasma jet, Tian et al.20 rst developed Al nanoparticles with a small fraction of AlN. From the presence of nanoparticles, Tang et al. identi ed that the growth mechanism of the as-synthesized AlN nanowires was largely based on a vapor–liquid–solid process.21 By using a solvent casting method, magnetoelectric (ME) nanocomposite lms composed of magnetostrictive CoFe2O4 nanoparticles with sizes between 35 and 55 nm embedded in P(VDF-TrFE) have been successfully prepared.22 It was discovered that ferroelectric and piezoelectric properties can be

Fig. 1 Zero-dimensional PNs.

Nanoscale

improved when a small amount of ferrite nanoparticles is added to the polymeric matrix. The inorganic BaTiO3 nanoparticles dispersed into the organic matrix was described by Capsal et al., and it is found that the dielectric permittivity of the composite highly increases with the volume fraction of nanoparticles.23

Ferroelectric BiFeO3 nanoparticles deposited on epitaxial substrates of SrRuO3 and La1 xSrxMnO3 were studied using band excitation piezoelectric response spectroscopy, piezoelectric response force microscopy, and ferromagnetic resonance.24 The dimensionality of domains within nanoparticles was found to be fractal in nature. Ferromagnetic resonance studies indicate that BiFeO3 nanoparticles only weakly a ect the magnetic response of La1 xSrxMnO3. The fabrication and piezoelectric characterization of poly(vinylidene uoride)–tri uoroethylene (PVDF–TrFE) thin lms enhanced with zinc oxide (ZnO) nanoparticles were proposed by Dodds et al.25 The results show that the incorporation of piezoelectric ZnO nanoparticles will enhance the bulk lm piezoelectricity while preserving the mechanical exibility of PVDF–TrFE. Prashanthi et al. integrated the ZnO nanoparticles into a photosensitive SU-8 polymer matrix to retain the highly desired piezoelectric properties of ZnO, and combined the photopatternability and the optical transparency of the SU-8 polymer.26 Hadji et al. applied the alumina nanoparticles dispersed in the copolymer P(VDF-TrFE) to obtain the high piezoelectric coe cient.27 Ahmed et al. investigated the nanoparticles of DySrIG, and found that they possess an electric memory e ect with thermalization, where their dielectric parameters have sensitive changes with temperature in the range 25–400 C and return to their original values at room temperature again.28 Fu et al. developed a new separator for lithium-ion batteries by depositing SiO2 ceramic layers of nanoparticles onto the polypropylene separators and using a simple yet e ective SiO2 formation and deposition process.29 (Bi0.5Na0.5)TiO3 doped with 8 mol% BaTiO3 particles with average size of 50 nm was compacted and sintered by spark-plasma-sintering method, and it is found that increasing the sintering temperature from 800 to 900 C can lead to the increase of piezoelectric coe cient d33.30

2.2One-dimensional (1D) PNs

One-dimensional (1D) PNs typically have a character dimension less than 100 nm and a length more than 1 mm. One-dimen- sional (1D) PNs (ZnO nanowires) created the rst nanogenerator prototype that converted ultrasonic waves into electricity.31 It is known that PNs most frequently used in self-powered nanosystems are piezoelectric nanowires.

In recent years, nano-wires (NWs) have found the most common applications. One-dimensional PNs o er the additional potential advantage of improved charge transport over zero-dimensional nanostructures such as nanocrystals. Compared with two-dimensional PNs, one-dimensional PNs used for mechanical energy scavenging have three unique advantages: enhanced piezoelectric e ect, superior mechanical properties, and high sensitivity to small forces.

Up to now, ZnO nanowires (NWs) have been the onedimensional PNs with the most interest. They are active

View Article Online

Review

components in applications such as piezoelectric nanogenerators, because the most critical piezoelectric polarization direction of ZnO NWs in applications is the c-axis. Most recently, Xu and Wang have presented a comprehensive overview of the progress that has been made in the one-dimensional ZnO nanostructures.16

To date, most of one-dimensional PNs are of circular, rectangle, or hexagonal cross-sections, as shown in Fig. 2. Most recently, lots of nanowires have been proposed, for example, ZnO nanowires,9,32–49 and nanotubes,50–56 ZnO nano- belts,57–67 ZnO nanorods,68,69 aluminum nitride (AlN) nanowires,3,70,71 PZT nano bers,72 and BaTiO3 nanowires.73–75 It was shown that ZnO nanotubes were approximately ve times more exible than the corresponding nanowires, which leads to the enhanced output voltage in nanogenerators.1 It is found that ZnO nanowires are superior over zincblende AlN and GaN wires for piezoelectric energy harvesting,76 so most research activities mainly focused on the piezoelectric ZnO nanowires. In addition, poly(vinylidene uoride) (PVDF) nano bers possess good piezoelectric property, and are attractive in energy conversion applications between electric and mechanical forms because of their low cost, high exibility and biocompatibility.77

Most recently, the rst self-powered system that works wirelessly and independently for long distance data transmission was driven by a nanogenerator utilizing densely grown ZnO nanowire textured lms.15

2.3Two-dimensional (2D) PNs

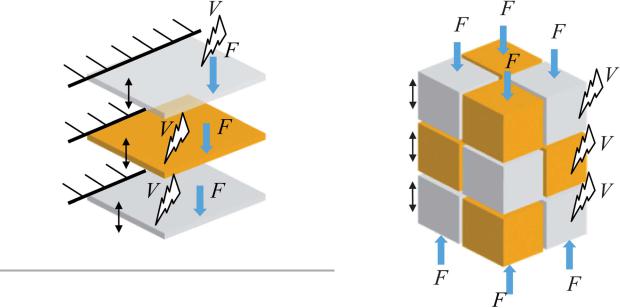
Two-dimensional PNs are lms (coatings) with nanometer thickness, as depicted in Fig. 3. Most recently, researchers have attempted to transfer piezoelectric nanoribbons and nano lms, for example, PZT and BaTiO3 materials, onto exible substrates for the purpose of utilizing the high electromechanical coupling of piezoelectric materials in conformable energy harvesting. Only some two-dimensional PNs have been proposed in recent years, i.e., PZT nano lms,78,79 ZnO nano lms,38,80 P(VDF-TrFE)– alumina nanolms,27,81,82 BaTiO3 nano lms,83 and PZT ribbons.84,85

Due to the high roughness factor and the large areas of exposed polar basal planes, the two-dimensional PNs show enhanced photocatalytic properties for decomposition of volatile organic compounds in comparison with common 1D nanowire arrays.

Fig. 2 One-dimensional PNs.

View Article Online

Nanoscale

Fig. 3 Two-dimensional PNs.

Review

electriceld components at the same position but also on all other points of the body. The scale coe cient regarded as a material parameter is introduced to incorporate the small scale factor. The nonlocal constitutive behavior can be represented by the following constitutive relation

where snlij (x) and slij(x0) are, respectively, the nonlocal stress tensor and local stress tensor, Dnlk (x) and Dlk(x0) are, respectively, the components of the nonlocal and local electric displacement. a(|x0 x|) is the nonlocal attenuation function which incorporates the constitutive equations at the reference point x produced by the local strain at the source x0, and rx0 xr is the Euclidean distance.

Based on the nonlocal theory and Timoshenko beam theory, Ke and Wang investigated the thermoelectric-mechanical vibration of the piezoelectric nanobeams.110 The in uences of the nonlocal parameter, temperature change, external electric voltage and axial force on the thermoelectric mechanical vibration characteristics of the piezoelectric nanobeams are discussed in detail.

Based on the nonlocal continuum piezoelasticity cylindrical shell theory, the transverse vibration analysis of uid-conveying double-walled boron nitride nanotubes subjected to combined electro-thermal loadings was developed in ref. 111.

In addition, the nonlocal piezoelectricity theory and surface/ interface piezoelectricity theory were combined to investigate the electromechanical coupling behavior of a cantilever piezoelectric nanowire, and an explicit formula for the electromechanical coupling coe cient of the piezoelectric nanowire was obtained.112

5 E ective material properties

These PNs exhibit enhanced piezoelectric e ect, excellent resilience and the unique coupling between piezoelectric and semiconducting properties. Ideally, piezoelectric materials should possess higher piezoelectric potential to power the piezoelectric nanogenerators. The piezoelectric potential can be derived from the e ective piezoelectric coe cient. The e ective piezoelectric coe cient40,56 is generally used as the gure of merit for judging how e ciently piezoelectric materials can harvest energy, because it is directly associated with the piezoelectric potential. The e ective piezoelectric coe cient can quantify the volume change when piezoelectric nanocomposites are subjected to an external electric eld (the inverse piezoelectric e ect) or the polarization generated upon application of an external stress (the direct piezoelectric e ect).

To achieve higher permittivity and piezoelectric properties of the composite, it is valuable for understanding the e ective electro-elastic properties piezoelectric nano-structures. The piezoelectric properties are considered to be closely related to

View Article Online

Nanoscale

both grain and domain sizes, and have become a current topic of great interest in recent research.

5.1Theoretical work

Coupling surface/interface theory has been widely used to characterize the e ective piezoelectric behavior of PNs, which has been reviewed in section 3.1. In this section, other theoretical work will be discussed.

In one-dimensional PNs, the polarization axis is the major piezoelectric potential accumulating axis, and is perpendicular to the substrate plane for the direct piezoelectric e ect; therefore, the relevant parameter associated with the piezoelectric potential is the e ective piezoelectric coe cient in that direction. Based on the nanoscale piezoelectric components, Sen et al. provided a detailed analytical treatment of the piezoelectric e ect on the elastic sti ness and piezoelectric polarization for a zincblende ZnO nanowire.76

By using a continuum model for ZnO NWs–NTs of di erent sizes, a theoretical model for calculating the radially dependent e ective piezoelectric coe cient and corresponding piezoelectric potential in intrinsic ZnO nanowires (NWs)–nanotubes (NTs) was presented in ref. 32. The dielectric and piezoelectric properties of the structured composites are well described by an analytical model for composites containing nanobers and particles arranged into chains. The in uence of degree of rotation and aspect ratio of the individual particles as well as their spacing is described in ref. 113.

Quantum mechanical computational estimates of piezoelectric coe cients in nanowires were reported in ref. 47. It revealed that the giant piezoelectric coe cients in both gallium nitride and ZnO nanowires is a result of size e ects. For gallium nitride, diameters well in excess of 2.5 nm are required to converge to bulk values.47

Atomistic calculation is a convenient way to obtain the e ective piezoelectric coe cient of PNs. This method has been used to analyze BaTiO3 nanoscale cantilever beams under bending deformation. Majdoub et al. presented the illustrative model problem of a nanoscale cantilever beam, and gave the analytical expressions for the ‘e ective’ or ‘apparent’ sizedependent piezoelectric coe cients and elastic modulus.114

In addition, nite element analysis was also used to analyze the output piezoelectric potential of a vertically compressed semiconductive ZnO NW.38

5.2Experimental work

To achieve improved piezoelectric and mechanical performance, many experimental methods are proposed to measure the response of PNs under various loading conditions. In the work of Dodds and his coworkers,25 the piezoelectric properties were measured by applying electric elds while measuring their response using a Sawyer-Tower circuit. Piezoelectric coe cient d33 measurements were performed with a Berlincourt type d33 meter (PM3000, PiezoTest, UK) with at electrodes.113 The e ective piezoelectric coe cient of a ZnO nanowire/nanobelt was experimentally measured by piezoresponse force microscopy, and ranged from 14.3 pm V 1 to 26.7 pm V 1 depending

Nanoscale

on the frequency, which is higher than the value for bulk ZnO of 9.93 pm V 1.56,115 By using UV-Vis absorption spectroscopy and Fourier transform infrared analysis, the variation of dielectric properties showed that the dielectric constant of PVDF–ZnO hybrid lms increases with increasing ZnO content at room temperature.116 In Loh and Chang's work, the experimental results suggest that increasing ZnO weight fraction leads to a near-linear increase in their dynamic strain sensitivity and piezoelectricity.117

Based on scanning probe microscopy, an experimental approach was used to directly quantify the three-dimensional piezoelectric response of individual GaN NWs.88 A nanoelectromechanical oscillator was used to measure the e ective piezoelectric coe cient of the ZnO nanowire growing along the c-axis.40 Piezoresponse force microscopy was used to measure the e ective piezoelectric coe cient (d33) of an individual (0001) surface-dominated zinc oxide nanobelt lying on a conductive surface.56

6 Synthesis of piezoelectric nano-structures

In this section, di erent synthesis techniques and growth mechanisms of piezoelectric nano-structures are summarized. Generally, the synthesis of PNs has seen rapid developments in recent years, especially the synthesis of piezoelectric nanowires. Novel fabrication techniques are constantly experimented and developed. To date, the experimental work mainly focused on the one-dimensional PNs. The basic synthetic methodologies of one-dimensional PNs were brie y reviewed in ref. 16.

For PNs, the fabrication techniques to synthesize them may be classi ed into ve main classes.

6.1Sol–gel template method

This method is based on the hydrolysis and condensation reactions of molecular precursors such as metal alkoxides and inorganic salts. It typically entails the hydrolysis of a solution of precursor molecules to rstly obtain a suspension of colloidal particles (the sol) and the gel composed of aggregated sol particles. The gel is then thermally treated to yield the desired material. Sol–gel chemistry has recently evolved into a general and powerful approach for preparing inorganic materials. It has a number of advantages over many conventional synthetic procedures. For example, materials of high purity can be synthesized at lower temperatures. In addition, the homogeneous multi-component systems can be obtained by mixing precursor solutions. This allows for easy chemical doping of the prepared materials.

In the work of Cernea et al.,118 (Na0.5Bi0.5)TiO3 doped with 5 mol% BaTiO3 (NBT-BT0.05) nanopowder was prepared by sol–gel method. The piezoelectric constants dij were calculated from the kij, 3ii and SEjj by the relation of dij ¼ kij(3ii,Sjj) in which, Sjj is the elastic constants, 3ii is the free permittivity, and kij is the electromechanical coupling factor. Cernea and his coworkers also successfully fabricated BaTiO3 doped-(Na1/2Bi1/2)TiO3 piezoelectric ceramics,119 dense nanocrystalline (Bi0.5Na0.5)TiO3 ceramics doped with 5, 8, and 11 mol% BaTiO3,30 and BNT-BTx

View Article Online

Review

piezoelectric ceramics120 by the sol–gel and spark plasma sintering techniques.

In the work of Masud et al.,121 the La2NiMnO6 nanoparticles were synthesized by a sol–gel process, and the dielectric, magnetic and magnetocapacitive properties were analyzed. By using the sol–gel template method combined with laser interference lithography, a PZT nano-dot array was fabricated, and the material characterization was brie y discussed.122 (Bi0.5Na0.5)TiO3 doped with 8 mol% BaTiO3 (BNT-BT0.08) nanopowder with average particle size of 30 nm was prepared by an acetate-alkoxide sol–gel method.123 (Na0.5Bi0.5)0.94Ba0.06TiO3 piezoelectric ceramics124 and 0.4 mm thick Pb(Zr,Ti)O3 lms125 were also synthesized by the sol–gel technique. For onedimensional PNs, nano bers of barium titanate have been produced in ref. 126 by the electrospinning technique from a sol–gel precursor.

6.2Hydrothermal method

The hydrothermal method is a powerful method for the fabrication of one-dimensional nanostructures, o ering signi cant advantages such as controllable structures and a cost-e ective low-temperature substrate-independent technique that allows for easy integration.

For one-dimensional PNs, piezoelectric ZnO nanostructures, including nanowires, nanotowers, nanovolcanoes, nanorods, nanotubes, and nano owers, have been grown by using the hydrothermal technique.35,127–130 A low-frequency-vibration- based power generator using ZnO cylindrical nanowires with the diameters of 70 nm and lengths of 2.5 mm was grown by hydrothermal method for process integration and low cost.37 The performance of dye-sensitized solar cells (DSSCs) on ZnO nanorods which were prepared by hydrothermal and vapordeposition methods has been investigated in ref. 131.

Recently, BT and ST nanocube single crystals which grew with {100} crystalline faces were synthesized by using hydrothermal process.132–135 The BT and ST nanocubes were prepared by hydrothermal method and the water-soluble titanium complex method.134,135

6.3Solvent casting method

This method is mainly used to prepare piezoelectric nano lms. The exible lms were obtained by spreading the solution on a clean glass substrate.

Magnetoelectric nanocomposites were successfully produced using piezoelectric phase PVDF–TrFE and magnetostrictive phase CoFe2O4 nanoparticles by a simple solvent casting method. Ferroelectric and piezoelectric properties were improved when a small amount of ferrite nanoparticles was added to the polymeric matrix.22 Nanocomposites of polyvinylidene uoride (PVDF) and nano-ZnO were prepared using the solution casting method for di erent concentrations of nano-ZnO, and characterized by X-ray di raction and atomic force microscopy.116

Graphene oxide nanosheets (GOn)/PVDF nanocompositelms prepared with di erent graphene oxide loading via solution casting method were given by Achaby and his coworkers,81

Review

and the dispersion of GOn in the PVDF matrix was performed using a transmission electron microscope operated at an accelerated voltage of 120 kV. P(VDF-TrFE)–alumina compositelms containing various amounts of alumina nanoparticles have been prepared by solvent casting method.27 0–3 nanocomposites of PVDF with varying volume percentages of stron- tium-doped PZT have been synthesized using a combination of a modi ed solution casting process and the hot press technique.136,137

6.4Electrospinning technique

In general, electrospinning is a process with low productivity because the polymer solution has to be fed at relatively slow rates in order to obtain ultrathin bers. The method is based on the jet drawing from a polymer solution or melt by a strong electric eld. The electrospinning technique can enable the fabrication of continuous, individual or mat-assembled bers with submicrometer diameters. It is important to note that the electrospinning technique is a very e ective tool for controllingber deposition and producing twoand three-dimensionalber arrays. Compared with solvent casting method, the electrospinning technique shows better interaction with the polymer matrix.

Neareld electrospinning technology can be used to fabricate PVDF piezoelectric bers with an excellent piezoelectric property. It has been successfully used to fabricate PVDF (polyvinylidene uoride) piezoelectric nanobers mixed with additional multiwalled-carbon nanotubes,138 and poly(vinylidene uoride)-tri uoroethylene (PVDF–TrFE) thin lms enhanced with zinc oxide nanoparticles.114 The fabrication of photopatternable piezoelectric nanocomposites for MEMS by electrospinning technique was given in ref. 26. In the work of Pu et al.,139 it is found that electrospun PVDF bers have larger (about twice) piezoelectric coe cient than that of PVDF thinlms possibly due to fewer defects.

6.5Sintering technologies

High piezoelectric properties can be acquired by sintering technologies, for example, microwave sintering, spark plasma sintering and two-step sintering, which were also attributed to the small grain size. The most novel and increasingly used method is spark plasma sintering, which has clear advantages over conventional sintering methods, making it possible to sinter nanometric powders to near full densi cation with little grain growth. This has become increasingly important recently, with the miniaturization of electronic devices and the requirement of investigating the size e ects on the properties approaching the nanometer scale.140–142

ZnO nanowires,49 ceramics,143 nanostructured ceramics of 0.92PbZn1/3Nb2/3O3–0.08PbTiO3,144 and BaTiO3 piezoelectric ceramics145 have been successfully prepared by this technology. Two-step sintering was applied to manufacture ne-grain barium titanate (BaTiO3) piezoelectric ceramics from hydrothermally synthesized 100 nm particles.146

In addition to the above methods, other synthesis techniques, such as sweeping-printing method,147 wet chemical

View Article Online

Nanoscale

methods,148 and capillary-force-assisted solution self-assembly method,149 were also proposed to fabricate the PNs.

In the reviewed experiments, the composition and crystallinity of these PNs were mostly determined by transmission electron microscopy (TEM), scanning electron microscopy (SEM), X-ray di raction (XRD), and Raman spectroscopy. SEM is an e cient way of getting the image of dispersion state in PNs.

7 Summary and future outlook

In this review, the classi cation of piezoelectric nano-structures and their potential nanoelectronic applications are presented, and some important formulations and experimental developments about synthesis techniques are revealed. As a new emerging class of nanocomposites, PNs have seen rapid developments in recent years. Novel fabrication techniques are constantly experimented and developed. Nevertheless, the theoretical and experimental works still need further exploration in the future.

A further investigation on the nonlocal piezoelectric is necessary to expand the theoretical foundation. The characterization of surfaces and interfaces of actual PNs is still controversial. Further experimental measurements in PNs are required to validate the two fundamental theories.

Only a few investigations on 3D PNs were reported in last two years, and more theoretical and experimental works are required to explore the wide application of the 3D e ect on PNs.

In addition, many fundamental questions and phenomena related to the growth mechanism of PNs are still not well understood and need further investigation. In fact, this eld leaves plenty of room to be explored, and therefore more studies and advances are anticipated.

Besides the piezoelectric e ect, the magnetoelectric (ME) e ect in nanostructures provides wide opportunity for the mutual control and detection of magnetization and electrical polarization in ferroelectromagnetic nanocomposites. This also needs a wide investigation.

Acknowledgements

This work is supported by the National Natural Science Foundations of China (no. 11272222; 11172185), the National Key Basic Research Program of China (no. 2012CB723300), and the Program for Changjiang Scholars and Innovative Research Team in University (no. IRT0971).

References

1C. Sun, J. Shi and X. Wang, J. Appl. Phys., 2010, 108, 034309.

2L. C. Lew, Y. Voon and M. Willatzen, J. Appl. Phys., 2011, 109, 031101.

3B. Sen, M. Stroscio and M. Dutta, J. Appl. Phys., 2012, 112, 024517.

4K. I. Park, S. Xu, Y. Liu, G. T. Hwang, S. J. Kang, Z. L. Wang and K. J. Lee, Nano Lett., 2010, 10, 4939.