Практикум по линейной алгебре и аналитической геометрии в среде МАТЛАБ.

Модуль 3. Кривые и поверхности второго порядка

Лабораторный практикум 3.1 Метод координат.

Авторы: кафедра ВМ-1

Модуль 3. Кривые и поверхности второго порядка.

Оглавление

Лабораторный практикум 3.1. Метод координат. 2

1.Системы координат. 2

2.Понятие уравнения линии 3

3.Построение линий различных порядков на плоскости. 5

4.Поворот системы координат 8

5.Задание на «5» 11

Лабораторный практикум 3.1. Метод координат.

1. Системы координат. 2 .Построение линий различных порядков на плоскости. 3. Поворот системы координат.

1. Системы координат.

Декартовой системой координатобычно называют прямоугольную систему координат, с одинаковым масштабом по осям координат. В плоскости она задается двумя взаимно перпендикулярными осями(ось абсцисс) и(ось ординат), пересекающимися в одной точкеO, называемой началом координат. Таким образом, положение любой точкина плоскости однозначно определяется двумя числами: первое число- величина проекции точки на первую ось (взятая с плюсом, если проекция попала на «положительную» часть оси, или с минусом, если на «отрицательную»), а второе число- величина проекции на вторую ось. Эти числа называются декартовыми координатами точки. Записьозначает, что точкаимеет декартовые координаты на плоскостии.

Говорят, что на плоскости введена полярная системакоординат, если заданы:

1. некоторая точка O, называемая полюсом;

2. некоторый луч , исходящий из точкиOи называемыйполярной осью.

Полярными координатами точки M называют два числа:полярный радиуси полярный угол -угол, на который следует повернуть ось для того, чтобы ее направление совпало с направлением вектора. Записьозначает, что точкаимеет полярный координатыи.

Пусть на плоскости введены:

правая декартовая система координат

(т. е. такая, что кратчайший поворот от оси к осипроисходит против часовой стрелки)

и полярная система ,

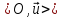причем полярная ось совпадает с положительной полуосью абсцисс. Тогда связь между декартовыми и полярными координатами произвольной точки задается формулами

; или.

MATLABимеет встроенные команды для покоординатного перевода из одной системы координат в другую. Так, например, «cart2pol» переводит из картезианской (декартовой) системы координат в полярную или цилиндрическую систему координат в зависимости от числа аргументов.

Упражнение 1.

1. Наберите в командном окне « helpcart2pol»

help cart2pol

С помощью команды «[phi,r]=cart2pol(3,3)» мы можем получить полярные координаты некоторой точки с декартовыми (Cartesian- картезианскими) координатами (3;3).

[phi, r]=cart2pol(3,3)

phi =

0.7854

r =

4.2426

r=sqrt(3^2+3^2)

r =

4.2426

phi=pi/4

phi =

0.7854

Выводы:

Действительно, у точки с координатами (3,3) расстояние до начала координат

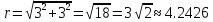, а угол отклонения.

2. Наберите в командном окне « helppol2cart»

helppol2cart

С помощью команды «[x,y]=pol2cart(-pi/4, 2*sqrt(2))» мы можем получить декартовые координаты некоторой точки с полярным угломи радиусом длины. Мы должны будем получить декартовые координаты (2, -2).

[x,y]=pol2cart(-pi/4,2*sqrt(2))

x=

2

y=

-2

Выводы:

Как и следовало ожидать точка с полярными координатами будет располагаться в четвертом квадранте координатной плоскости.

2. Понятие уравнения линии

Предположим, что на плоскости задана декартова прямоугольная система координат и некоторая линия.

Рассмотрим уравнение , связывающее две переменныеи.

Уравнение называется уравнением линииотносительно заданной системы координат, если уравнениюудовлетворяют координатыилюбой точки, лежащей на линии, и не удовлетворяют координатыини одной точки, не лежащей на линии.

Согласно этому определению сама линия представляет собойгеометрическое место точек, координаты которых удовлетворяют уравнению

Если в заданной системе координат уравнение является уравнением линии, будем говорить, чтоопределяет линию.

Уравнение является уравнением окружности радиусас центром в точке.

Линия называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением, в котором– алгебраический полином (т.е. сумма конечного числа слагаемых вида,– целые,– некоторая постоянная).

Если при этом – алгебраический полином порядка, линияназываетсялинией порядка .

Например, окружность – алгебраическая линия второго порядка.

- полярное уравнение n-лепестковой розы

При n=3,a=1 полярное уравнение трех лепестковой розыв декартовой системе координат представляет собой алгебраическое уравнение 4 порядка.

Возьмем функцию , заданную в полярных координатах, и попытаемся представить ее в виде уравнения в декартовых координатах.

=.

. |*

.

Таким образом, получаем уравнение той же линии (трех лепестковой розы)

Но наиболее ценным, полезным и неожиданным будет представление в декартовой системе координат одно лепестковых роз.