§ 4. Ортогональное дополнение

Пусть – подпространство конечномерного евклидова пространстваОртогональным дополнением подпространства называется множество

(12)

Таким образом, состоит из всех векторов, ортогональных всем векторам изНетрудно доказать, чтоявляется подпространством пространстваКроме того, имеет место утверждение.

Теорема. Если – конечномерное евклидово пространство и– его подпространство, то любой векторпредставим в виде

(13)

где причём такое представлениеединственно.

Вектор в формуле (13) называетсяортогональной проекцией вектора на подпространствоа вектор–ортогональной составляющей (см. рис. 1). Равенство (13) показывает, что пространство раскладывается в сумму подпространствиЕсли каждый элемент суммы двух подпространствираскладывается в сумму векторов изиединственным образом, то говорят, что эти подпространства образуют прямую сумму и записывают её в виде Таким образом, утверждение теоремы состоит в том, что для любого подпространстваевклидова пространстваимеет место разложение в прямую сумму

(14)

Ещё одно интересное свойство состоит в том, что понятие ортогонального дополнения является взаимным: если второе подпространство есть ортогональное дополнение к первому, то первое будет являться ортогональным дополнением ко второму:

(15)

Замечания. 1. Из формулы (14) следует, что если – базис подпространстваа– базис его ортогонального дополнениято множествобудет являться базисом пространстваДля размерностей этих пространств имеет место равенство

(16)

2. Если – произвольное подмножество евклидова пространстват.е.необязательно является подпространством, то всё равно можно определитьПри этомбудет являться подпространством, но, конечно, сформулированная выше теорема теперь верна не будет, а равенства (14), (16) потеряют смысл.

3. Всё вышесказанное справедливо для конечномерного унитарного пространства.

4. В бесконечномерном случае равенства (14) и (15) верны не для всех подпространств. Но равенства сохраняются и в бесконечномерном случае.

Опишем теперь процесс нахождения ортогональной проекции и ортогональной составляющей вектора. Пусть – евклидово пространство,– его подпространство иПусть– базис подпространства(не обязательно ортогональный). Запишем векторв видегдеТак кактоа так както мы имеем систему уравнений:Раскрыв скобки, получим:

(17)

Из этой системы можно найти числа из которых находим ортогональную проекциюОртогональная составляющаянаходится простым вычитанием:

Матрица системы (17)

называется матрицей Грама. Она невырожденна, если векторы линейно независимы (это нам дано в условии задачи). Таким образом, система (17) имеет единственное решение. Впрочем, это и так ясно ввиду того, что всякий вектор однозначно разлагается по базису

Вычисления сильно упрощаются в случае, если базис пространстваявляется ортонормированным. Еслито матрица Грама есть единичная матрица. Следовательно,Коэффициентыназываютсякоэффициентами Фурье. Алгоритм нахождения проекции вектора теперь можно сформулировать следующим образом.

1. Находим коэффициенты Фурье вектора по формулам

(18)

2. Вычисляем ортогональную проекцию векторана подпространствопо формуле

Задача 7. Найти ортогональную проекцию вектора пространствана подпространство, порождённое векторами

Решение. Найдём скалярные произведения: и аналогичноДалее,Подставим эти цифры в систему (17):

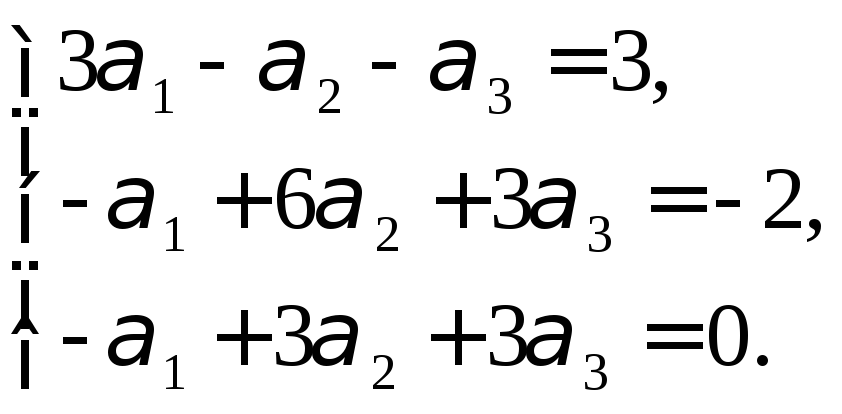
Решив эту систему, получим: Найдём ортогональную проекцию:

Наконец, найдём ортогональную составляющую:

Задача 8. Найти базис ортогонального дополнения подпространстванатянутого на систему векторов

Решение. Вектор принадлежит в том и только том случае, если он удовлетворяет системе уравнений

Найдём фундаментальную систему решений этой системы: Она и будет базисом пространства