4.1. Преобразования с использованием записи базиса в виде матрицы-строки.

Рассмотрим примеры, в которых получим формулы преобразования координат при переходе от базиса к базису с использованием формы (8).

Так как система векторов линейно зависима (число векторов равно (n+1), т.е. больше размерности пространства), то можно получить разложение вектора в базисе :

, (10)

где - координаты вектора в базисе .

Применяя форму (8) записи систем векторов базисов и выражение (10) можно представить в виде:

= , (11)

или в компактной форме: .

Матрицу С₁ называют матрицей перехода от базиса к базису с использованием формы (8).

4.1.1. Нахождение матрицы перехода от одного базиса к другому.

Рассмотрим примеры, в которых получим формулы для вычисления матрицы перехода от базиса к базису с использованием формы (8).

☺ Пример 107. Пусть задан некоторый базис , и через его векторы определены еще два базиса: и : Необходимо построить матрицу переходе от базиса к , если:

, (12)

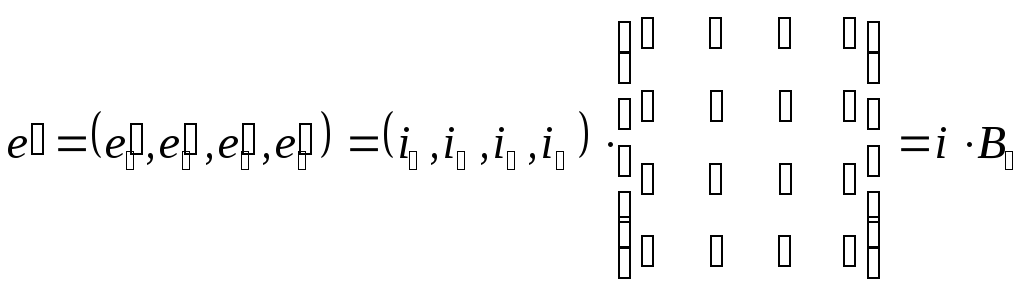, (13)

Решение: Представим записи (12) и (13) в компактной форме:

→ ,

, → ,

где С₁ – искомая матрица перехода от базиса к .

Последнее (если учесть, что , где Е – единичная матрица, и то, что ) можно записать в виде:

.

В последней записи матрица является искомой матрицей перехода.

Ответ: матрица перехода от базиса e к базису есть матрица (см. решение задачи).

Пример 108. Пусть задан некоторый базис , и через его векторы определены еще два базиса: и : Необходимо построить матрицу переходе от базиса к , если:

, (14)

, (15)

Решение: Представим записи (14) и (15) в компактной форме:

→ ,

, → ,

где –матрица перехода от базиса к :

,

Ответ: матрица перехода от базиса e к есть матрица (см. решение задачи).

4.1.2. Преобразование координат вектора при переходе к новому базису.

Пусть в линейном пространстве R в базисе задан вектор a :

, (16)

или в форме , (17) представляющей координаты вектора a в виде матрицы-столбца (по другому записать матричное выражение (17) было бы невозможно).

Этот же вектор a в линейном пространстве R в базисе имеет вид:

, (18)

или в форме . (19)

Учитывая (16) и (18) для вектора a получаем тождественную запись:

, (20)

откуда следует:

→ , (21)

где - обратная матрица для матрицы С₁ перехода от старого базиса к новому, или в иной форме:

, . (22)

☺ Пример 109. Пусть линейное пространство R трехмерное с базисом и в нем задан вектор . В рассматриваемом пространстве задан еще один базис:

,

где С₁ – матрица перехода от базиса к базису .

Требуется найти координаты вектора a в базисе .

Решение: В соответствии с формулой (17) для вычисления координат вектора a в базисе требуется вычислить для матрицы перехода С₁ обратную матрицы. Ее можно найти любым их способов, рассмотренных в Гл.4, § 2:

,

Используя найденную матрицу , запишем строку координат вектора a в базисе :

,

т.е.

Ответ: .

Пример 110. Пусть задан некоторый базис , и через его векторы определены еще два базиса: и :

,

,

Необходимо составить формулу преобразования координат вектора при переходе от базиса к .

Решение: В Примере 107 была получена матрица С₁ перехода от базиса к базису :

,

В соответствии с формулой (18) для вычисления координат вектора х необходимо вычислить обратную матрицу . Применяя один из способов вычисления обратных матриц, получаем выражение для :

. (23)

Если теперь присваивать параметрам некоторые значения, то будем получать определенные координаты вектора х в базисе .

Ответ: ..

Пример 111. Пусть задан некоторый базис , и через его векторы определены еще два базиса: и : Необходимо построить матрицу переходе от базиса к , если:

, (24)

, (25)

Необходимо составить формулу преобразования координат вектора при переходе от базиса к .

Решение: В Примере 108 была получена матрица С₁ перехода от базиса к базису

,

В соответствии с формулой (18) для вычисления координат вектора х необходимо вычислить обратную матрицу . Применяя один из способов вычисления обратных матриц, получаем выражение для :

. (26)

Если теперь присваивать параметрам некоторые значения, то будем получать определенные координаты вектора х в базисе .

Ответ: ..

☻Решите примеры:

Пример 112. Пусть R линейное 4-мерное пространство с базисом и в нем задан вектор . В рассматриваемом пространстве задан еще один базис:

,

где С₁ – матрица перехода от базиса к .

Требуется найти координаты вектора a в базисе .

Ответ: .

Пример 113. Пусть R линейное 4-мерное пространство с базисом и в нем задан вектор . В рассматриваемом пространстве задан еще один базис:

,

где С₁ – матрица перехода от базиса к .

Требуется найти координаты вектора a в базисе .

Ответ: .