матанколобок / таблица по тригонометрии

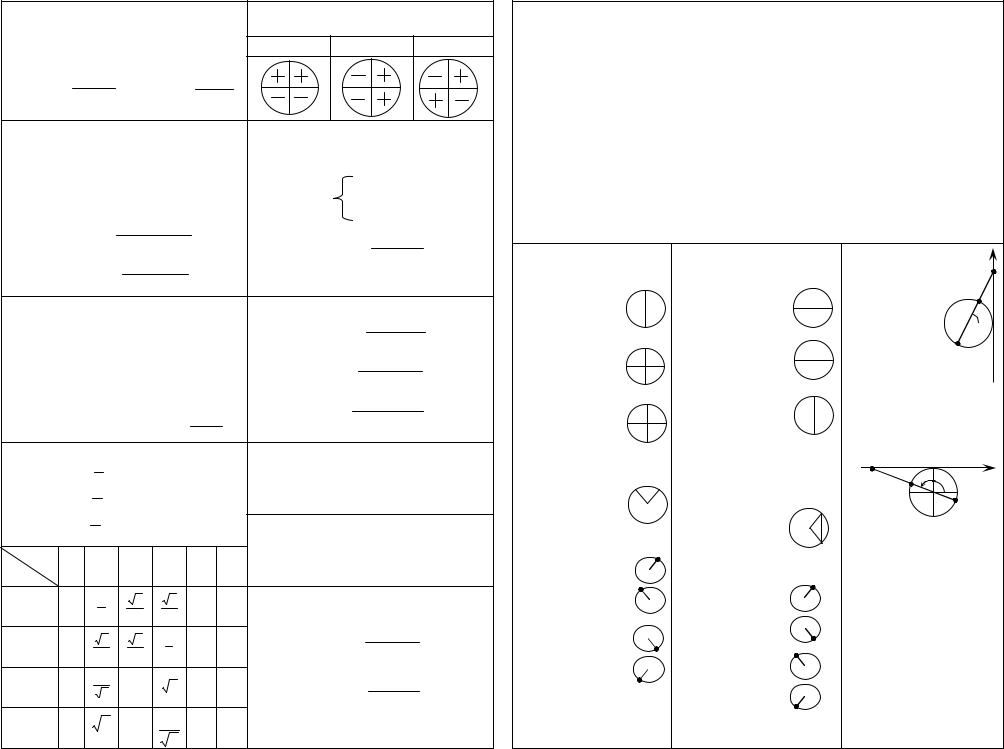
Основные тригонометрические

Знаки значений

тождества

тригонометрических функций

sin2 α + cos2 α = 1 ;

tg α.ctg α = 1

sinα

cosα

tgα; ctgα

1+ tg2 α =

1

; 1 + ctg2 α =

1

cos 2 α

sin 2 α

Формулы сложения

Формулы двойного угла

cos (α + β) = cos α.cos β – sin α.sin β

sin 2α = 2.sin α.cos α

cos (α– β) = cos α.cos β + sin α.sin β

cos2 α − sin2 α

sin (α + β) = sin α.cos β + cos α.sin β

cos 2α =

2.cos2 α −1

sin (α – β) = sin α.cos β –

cos α.sin β

1 − 2.sin2 α

tgα + tgβ

tg (α+β) =

2 tgα

1 − tgα tgβ

tg2α =

1− tg2α

tgα −tgβ

tg (α−β) = 1+ tgα tgβ

Преобразование суммы в произведение

Формулы понижения степени

sin α + sin β = 2.sin α + β . cosα − β

cos2 α = 1+ cos 2α

2

2

2

sin α −sin β = 2.sin α − β . cosα + β

sin

2

α

1− cos 2α

2

2

=

2

cos α +cos β = 2.cosα + β . cos α − β

1 − cos 2α

2

2

.

α + β .

β −α

tg2 α =

cos α −cos β =2

1 + cos 2α

sin

2

sin

2

Преобразование произведения в сумму

Следствие из формул понижения степени

sin α.cos β =

1

(sin(α−β)+sin(α+β))

1 + cos 2α =

2.cos2 α

2

1 – cos 2α

2.sin2

α

cos α.cos β =

1

(cos(α−β)+cos(α+β))

=

2

sin α.sin β = 12

(cos(α−β)−cos(α+β))

Формулы тройного угла

α

π

π

π

π

cos 3α = 4.cos3 α - 3.cos α

0

π

sin 3α = 3.sin α - 4.sin3 α

6

4

3

2

sin α

0

1

2

3

1

0

Формулы универсальной

2

подстановки

2

2

2 tgα

cos α

3

2

1

sin 2α=

1

0

-1

2

2

2

2

1+ tg α

tg α

0

1

1

3

-

0

cos 2α=

1−tg2α

3

1+tg2α

ctg α

-

3

1

1

0

-

3