Этот метод состоит в последовательных расчетах по формулам k1 = f (xm , ym ) ,

начиная с точки (x0 , y0 ) .

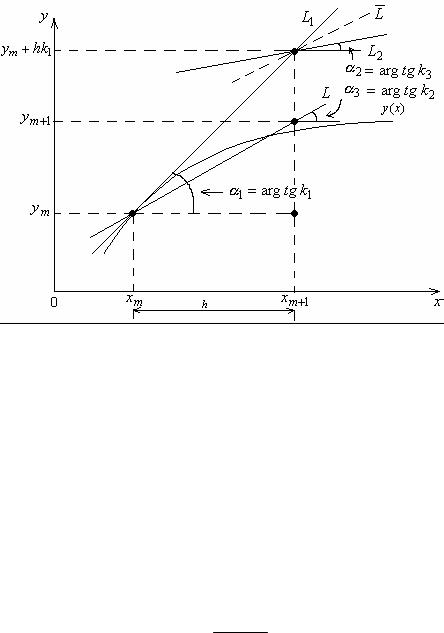
Формулы Рунге–Кутта 2-го порядка (6.4) иллюстрируются рис. 6.2.

Рис. 6.2

В точке (xm , ym ) проводится касательная к интегральной кривой y = y(x) (прямая L1) и определяется тангенс угла наклона (угловой коэффициент) этой касательной k1 . Аналогично методу Эйлера определяется новая точка

(xm + h, ym + hk1). В этой точке проводится касательная с угловым коэффици-

ентом k2 (прямая L2 ). Новое значение функции ym+1 определяется как точка пересечения касательной с усредненным угловым коэффициентом

k3 = k1 +2 k2