30

Методические указания

к проведению практических занятий по дисциплине

«Физика наноразмерных полупроводниковых структур»

Семинар 1

С1. Аналитический расчет короткоканального эффекта в МОПТ

План семинара

С1.1 Короткоканальный эффект

С1.2 Понижение барьера, индуцированное стоком (DIBL)

С1.3 Уравнение Пуассона и латеральное проникновение электрического поля

С1.4. Постановка проблемы aналитического решения уравнения Пуассона с упрощенными граничными условиями для расчета ККЭ в подпороговой области

С1.5 Метод решения

С1.6. Короткоканальный спад напряжения

С1.7. Анализ спада порогового напряжения

С1.8. Короткоканальный подпороговый наклон и чувствительность к подложке

С1.9. Экстремально ретроградное легирование (Ground-Plane) МОПТ

С1.10 Обобщенная длина масштабирования для high-k диэлектриков

Литература

Задание для СРС

Приложение 1 к семинару 1. Обобщенная модель длины масштабирования МОПТ

П1.1 Уравнение для длины масштабирования в модели двух областей

П1.2 Уравнение для длины масштабирования модели трех областей

П1.3 Ортогональность кусочно-линейных собственных функций

Литература к Приложению 1

С1.1 Короткоканальный эффект

Из выражений (3.26), (3.28) для выходных ВАХ длинноканального МОПТ видно, что для данного напряжения питания ток МОПТ увеличивается с уменьшением длины канала. Однако длина канала не может быть произвольно уменьшена, даже если это позволяет литография, вследствие проявления короткоканального эффекта (ККЭ).

Рис.С1.1 Короткоканальный спад порогового напряжения: экспериментальные значения порогового напряжения п- и рМОПТ в зависимости от длины канала [1].

Короткоканальный эффект заключается в уменьшении порогового напряжения МОПТ при уменьшении длины канала (рис.С1.1). ККЭ особенно выражен, когда напряжение на стоке близко к напряжению питания. В технологии КМОП СБИС длина канала изменяется статистически от чипа к чипу, от пластины к пластине, и от партии к партии вследствие допусков процесса. Следовательно, важно обеспечить, чтобы пороговое напряжение вследствие ККЭ не становилось слишком низким для приборов с минимальной длиной канала на чипе.

Ключевое различие между короткоканальным и длинноканальным МОПТ в том, что рисунок поля в обедненной области короткоканального МОПТ двумерен. Эквипотенциали в длинноканальном приборе почти совершенно параллельны границе раздела оксид-кремний, или в направлении длины канала (оси у), так что электрическое поле (вертикальное, или в направлении оси х) одномерно в большей части прибора. В короткоканальном приборе эквипотенциали криволинейны, и результирующий рисунок электрического поля двумерен. Другими словами, обе компоненты электрического поля, х и у, существенны в короткоканальном МОПТ. Моделирование МОПТ показывает, что для данного затворного напряжения в короткоканальном приборе имеется больший изгиб зон (выше ) на границе оксид-кремний, чем в длинноканальном. Ширина обедненной области также шире в короткоканальном случае. Все это указывает на меньшее пороговое напряжение в короткоканальном приборе.

Двумерный характер поля в короткоканальном приборе возникает от близости областей стока и истока. Наряду с обедненной областью под затвором МОПТ, имеются также обедненные области, окружающие переходы стока и истока. В длинноканальном приборе исток и сток достаточно отделены друг от друга, так что их обедненные области не влияют на рисунок потенциала или поля в большей части прибора. В короткоканальном приборе расстояние исток-сток сравнимо с глубиной обеднения МОП-структуры в вертикальном направлении, и напряжение исток-сток сильно влияет на изгиб зон в значительной части прибора.

С1.2 Понижение барьера, индуцированное стоком (DIBL)

Физика ККЭ может быть понята под другим углом зрения при рассмотрении потенциального барьера (для электронов в пМОПТ) на поверхности между истоком и стоком, как показано на рис.С1.2. В выключенном состоянии МОПТ этот потенциальный барьер (область р-типа) препятствует протеканию тока электронов к стоку. Поверхностный потенциал контролируется главным образом напряжением на затворе. Когда это напряжение меньше напряжения порога, только ограниченное число электронов, инжектированных из истока, способно преодолеть барьер и достичь стока (подпороговый ток). В длинноканальном приборе барьер плоский в большей части прибора. Поля истока и стока действуют только в очень узких областях на концах канала. Однако когда длина канала уменьшается, поля истока и стока проникают глубоко в канал, что приводит к понижению потенциального барьера между истоком и стоком. Это вызывает существенное увеличение подпорогового тока. Другими словами, пороговое напряжение становится ниже, чем в длинноканальном приборе. Область максимального потенциального барьера также сокращается до одной точки вблизи центра прибора.

Рис.С1.2. Энергия дна зоны проводимости в зависимости от расстояния (нормированного на длину канала L) от истока к стоку для длинноканального (А) и короткоканального МОПТ при низком напряжении стока (В) и высоком напряжении стока (С). Напряжение на затворе одинаково для всех трех случаев [2].

Когда к прибору прикладывается высокое напряжение стока, высота барьера уменьшается еще больше, вызывая дальнейшее уменьшение порогового напряжения. Точка максимума барьера также сдвигается в направлении истока, как показано на рис.С1.2. Этот эффект называется понижением барьера, индуцируемое стоком (drain-induced barrier lowering − DIBL). Это объясняет экспериментально наблюдаемое увеличение подпорогового тока с увеличением напряжения стока в короткоканальных МОПТ. Рис.С1.3 показывает подпороговые характеристики длинно- и короткоканальных МОПТ при различных напряжениях стока.

Рис С1.3. Подпороговые характеристики длинно- и короткоканальных МОПТ при различных напряжениях стока [3].

В длинноканальном приборе (L=2мкм) подпороговый ток не зависит от напряжения стока (). В короткоканальном приборе (L=0,35мкм) кривая ВАХ при увеличении смещения стока сдвигается параллельно в сторону более низкого порогового напряжения. При ещё более коротких длинах канала (L=0,2мкм) подпороговый наклон начинает деградировать (уменьшаться), так как поверхностный потенциал теперь контролируется больше стоком, чем затвором. В конце концов, прибор достигает условия, когда затвор полностью теряет контроль над каналом и высокий ток стока продолжает существовать независимо от напряжения затвора.

С1.3 Уравнение Пуассона и латеральное проникновение электрического поля

Дальнейшего понимания роли латерального электрического поля в короткоканальных МОПТ можно добиться путем исследования двумерного уравнения Пуассона

. (С1.1)

В обедненной области МОПТ плотность подвижных носителей пренебрежимо мала. Нужно принимать во внимание только ионы акцепторов. Для равномерно легированной подложки с концентрацией примеси , уравнение Пуассона может быть записано в виде

(С1.2)

где − электрическое поле в вертикальном направлении. Заряд обедненного слоя, возникающий от ионизированных акцепторов, можно рассматривать состоящим из двух частей: первая часть,, управляется полем затвора в вертикальном направлении; вторая часть,, управляется полем исток-сток в латеральном направлении. В длинноканальных приборах латеральное поле пренебрежимо мало в большей части канала, и почти весь заряд обедненной области управляется полем затвора. В короткоканальном приборе продольное поле становится существенным. Рис С1.3.а показывает пример распределения продольного поля вдоль длины канала, полученного путем двумерного численного моделирования. Продольное поле максимально на истоковом и стоковом переходах, экспоненциально уменьшаясь по направлению к середине канала.

При низких напряжениях стока поля истока и стока взаимно уничтожают друг друга точно в центре прибора. При уменьшении длины канала постоянная экспоненциального спада остается неизменной, в то время как величина продольного поля вблизи середины прибора значительно возрастает. Это отражает проникновение полей истока и стока в область канала короткоканального МОПТ. Ниже будет показано, что характеристическая длина

экспоненциального спада продольного поля равна (С1.24),где − глубина обедненной области. Приложение высокого напряжения стока (рис. С1.3.b) не изменяет поле истока, но увеличивает поле стока. Это сдвигает точку нулевого поля в сторону истока, делая рисунок поля асимметричным, и в то же время повышая еще больше величину поля. Точка нулевого поля соответствует точке наименьшей толщины слоя обеднения, также как и точке максимума энергетического барьера на рис.С1.2.

Рис. С1.3. Моделирование продольного поля как функции расстояния вдоль горизонтального сечения обедненного слоя для (а) длинно- и короткоканальных приборов и (b) низком и высоком смещениях стока [4].

С1.4. Постановка проблемы aналитического решения уравнения Пуассона с упрощенными граничными условиями для расчета ККЭ в подпороговой области

ККЭ – очень сложная математическая задача, включающая проблему неоднородных двумерных граничных условий. Чтобы упростить проблему граничных условий до выполнимого уровня, мы сделаем несколько предположений. Упрощенная геометрия короткоканального МОПТ представлена на рис.С1.4. Область определения – прямоугольный бокс с длиной, равной длине канала L, определяемой как расстояние между истоком и стоком (рис.С1.4). В вертикальном направлении бокс состоит из области оксида, толщиной и области кремния, определяемой толщиной обедненного слоя.

Рис. С1.4 Упрощенная геометрия для аналитического решения уравнения Пуассона в короткоканальном МОПТ. Затемненные площади в подложке представляют собой проводящие области постоянного потенциала [4].

Ось х направлена вертикально, ось у – горизонтально, начало координат в точке А. Потенциал определяется как потенциал в точке (х,у) относительно потенциала р-подложки. Подложка предполагается равномерно легированной с концентрацией N_a. В области окисла AFGH уравнение Пуассона переходит в уравнение Лапласа

. (С1.3)

В подпороговой области концентрация подвижных носителей в обедненной области кремния (и дырок, и электронов) предполагается пренебрежимо малой. Поэтому уравнение Пуассона имеет вид

. (С1.4)

Длина области кремния равна длине канала L. Глубина обедненного слоя, , будет определена позднее.

Как следует из условия (закон Гаусса), нормальная компонента электрического поля изменяется с коэффициентомпри переходе через границу кремний-окиселAF. Чтобы исключить это граничное условие, так чтобы и его производные были непрерывны, окисел заменяется некоторой эквивалентной областью с той же самой диэлектрической постоянной, что и у кремния, но с толщиной, равной. Это сохраняет емкость и позволяет рассматривать прямоугольную область как гомогенный (однородный) материал с высотойи диэлектрической постоянной. Это является хорошим предположением, когда оксид тонок по сравнению с толщиной обедненной области, как это имеет место в большинстве реальных технологий. Недостатком такого подхода может быть некоторая ошибка в тангенциальной (по осиу) компоненте поля, величина которой не изменяется на границе окисел-кремний. Ошибка ожидается малой, когда толщина подзатворного окисла значительно меньше толщины обедненной области , так что в окисле доминирует нормальная компонента.

Если мы предполагаем, что переходы стока и истока резкие и глубже, чем ¹, мы можем записать следующий набор упрощенных граничных условий:

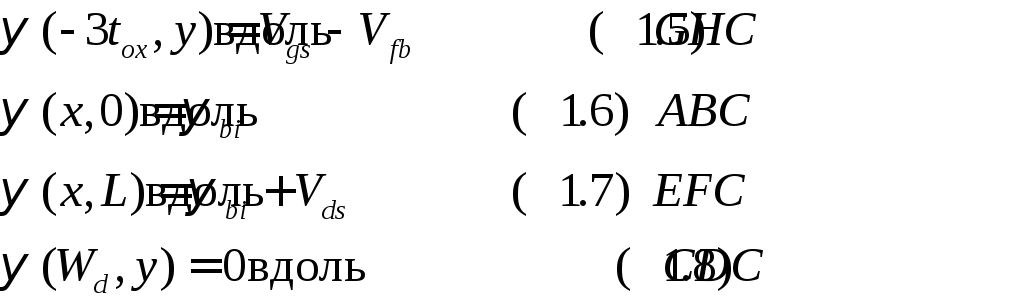
где и − напряжения на затворе и стоке, − напряжение плоских зон, и − контактная разность потенциалов переходов стока и истока. Для резкогоп+-р перехода . Типично. Если имеется смещение, тозаменяется нав выражениях (С1.6) и (С1.7) и− нав выражении (С1.5). Нижняя граница фактически подвижна, так какизменяется с изменением напряжения . Расстояние ВС приблизительно определяется толщиной ОПЗ перехода истока

. (С1.9)

Подобным же образом расстояние DE определяется толщиной ОПЗ перехода стока

. (С1.10)

Граничные условия для потенциала вдоль FG и HA предполагают линейное изменение между значениями в конечных точках, в то время как вдоль BC и DE предполагается параболическое изменение между конечными точками.

С1.5 Метод решения

Метод решения использует принцип суперпозиции и заключается в представлении электростатического потенциала в виде следующих слагаемых:

. (С1.11)

Здесь − решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).,,− решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,равно нулю на верхней, нижней и правой границах, ноудовлетворяет левому граничному условию (С1.6). Подобным же образом,равно нулю на верхней, нижней и левой границах, ноудовлетворяет правому граничному условию (С1.7) и т.д.

Естественным выбором для [фактически] является решение для одномерного МОПТ, использующее приближение полного обеднения:

для области окисла , (С1.12)

и для области кремния. (С1.13)

Здесь − длинноканальный поверхностный потенциал, который изменяется с напряжением. Он связан с толщиной ОПЗформулой

, (С1.14)

чтобы удовлетворять выражению (С1.4). Заметим, что выражения (С1.12) и (С1.13) удовлетворяют верхнему и части CD нижнего граничных условий, [выражения (С1.5) и (С1.8)], и непрерывны при х = 0. Требование, чтобы было непрерывно прих = 0, позволяет найти соотношение между и:

, (С1.15)

где определяется выражением (С1.14). Заметим, что выражение (С1.15) совпадает с выражением для смещения затвора в подпороговой области:.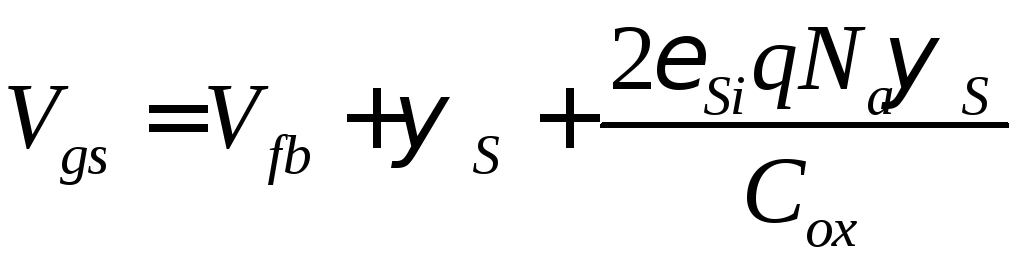

Остальные слагаемые решения в (С1.11) имеют следующую форму

, (С1.16)

, (С1.17)

. (С1.18)

Коэффициенты определяются из требования удовлетворения граничным условиям. Например, на левой границе

. (С1.19)

Для вычисления отдельных коэффициентов выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −до:

.(С1.20)

определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет только на отрезке. Чтобы дополнить значениядля неустановленного точно промежутка вдоль отрезкаНА на рис.С1.4, используется линейная интерполяция между значениями идля отрезка. Это хорошая аппроксимация, если ширина зазорамного меньше, чем.

В середине прибора, , члены виизменяются как. Если длина каналаL не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем

, (С1.21)

где . Так какмало по сравнению с, хорошей аппроксимацией является, так что

, (С1.22)

где для 15°45°. Подобным же образом коэффициент наименьшего порядка в рядуполучается из правого граничного условия

. (С1.23)

Третьим рядом, , можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (СD на рис. С1.4) уже удовлетворяет , следовательно, и. Остающийся вклад в коэффициентот сегментовВС и DE много меньше, чем или.

Приближенное аналитическое решение для области кремния в подпороговой области тогда

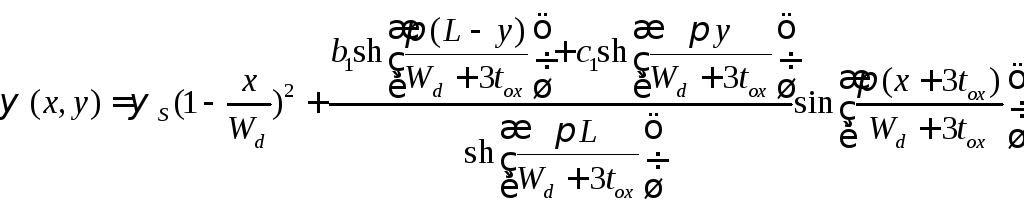.(С1.24)

Вычисление поля из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.3(а) и (b). Характеристическая длина экспоненциального спада равна , и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.

С1.6. Короткоканальный спад напряжения

В подпороговом режиме ток стока преимущественно диффузионный и контролируется в основном наивысшей точкой потенциального барьера вдоль канала для электронов, как показано на рис. С1.2. Пороговое напряжение для короткоканального прибора определяется как напряжение на затворе, при котором минимум электростатического потенциала (максимум барьера для электронов) на поверхности равен . Это происходит при напряжении на затворе ниже, чем пороговое напряжение длинноканального прибора на величину.

Чтобы найти величину спада порогового напряжения короткоканального прибора , мы рассмотрим потенциал на поверхности кремния,. Он имеет минимальное значение при, которое находится из решения уравненияс использованием аппроксимациидля:

(С1.25)

Эта точка соответствует точке максимальной высоты барьера на рис. С1.2. Она близка к середине канала, когда напряжение стока мало. Когда напряжение стока велико, точка наивысшего барьера движется ближе к истоку, как показывает рис. С1.3 (b).

В подпороговой области плотность инверсионного заряда изменяется экспоненциально с потенциалом в данной точке. Протекание тока контролируется наименьшим поверхностным потенциалом вдоль канала, то есть при . Подставляя (С1.25) в (С1.24) и полагая, мы получаем

. (С1.26)

Последний результат был получен подстановкой выражений (С1.22), (С1.23) и применением аппроксимаций и. В выражении (С1.26) первый член представляет длинноканальный поверхностный потенциал. Второй член происходит от граничных условий исток-сток. Он увеличивает поверхностный потенциал и способствует в короткоканальном приборе достижению условия порога,применьшем, чем длинноканальное значение порога. Так какуменьшается, величинатрансформируется в сокращение,, в соответствии с выражением. (см. выражения (3.1.2) и (3.1 3)), где− максимальная толщина обедненной области. Уменьшение порогового напряжения в короткоканальном приборе, следовательно, равно

(С1.27)

Заметим, что как установлено ранее, иесть максимальная толщина обедненной области при пороговом напряжении,. Зависимостьотприводит кDIBL-эффекту.

С1.7. Анализ спада порогового напряжения

Для типичных значений выражение (С1.27) дает величину спада короткоканальногоравную 100мВ для. Так как 100мВ вообще приемлемый (допустимый) наихудший спадв современных КМОП технологиях,минимальная приемлемая длина канала равна . Заметим, чтоесть эффективная высота прямоугольного бокса на рис.С1.4, иL – его ширина. Качественно суровость короткоканального эффекта измеряется аспектовым отношением прямоугольного бокса. Низкое аспектовое отношение, такое что , обеспечивает приемлемость короткоканальных эффектов.

Вследствие экспонененциальной зависимости спад порогового напряжения с уменьшением длины канала очень чувствителен к величине , которую можно определить как длину масштабированияМОПТ.Критерий минимальной длины канала тогда . Чтобы масштабировать МОПТ к более короткой длине канала с приемлемыми ККЭ, длина масштабирования должна быть сокращена соответствующим образом. Это означает уменьшение как , так ис тем же коэффициентом, что и длина канала. Заметим, что для равномерно легированной подложки величина

. (С1.28)

Зависимость отN_a представлена на рис.С1.5.

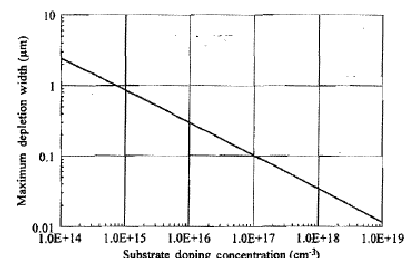
Рис.С1.5.Толщина обедненной области при условии в зависимости от концентрации примеси для равномерно легированной подложки [3].

Формула (С1.28) справедлива для длинноканальных приборов, когда не зависит отL. Это хорошее приближение для . Для более коротких длин каналаимеет тенденцию увеличиваться, когдаL уменьшается. Когда это происходит, не увеличивается так быстро с уменьшениемL, как показывает экспоненциальный член в выражении (С1.27). Для выражение (С1.27) с длинноканальной толщинойимеет тенденцию переоценивать спад порогового напряжения с коэффициентом. При агрессивном масштабировании в высокопроизводительных логических КМОП технологияхчасто устремляют к значению. Дляпредположение, что члены более высокого порядка вив разложении пренебрежимо малы, больше не справедливо. Такой прибор имеет слишком суровый ККЭ, чтобы мог быть использован на практике.

Вся вышеприведенная дискуссия предполагала, что глубины истокового и стокового переходов больше, чем толщина обедненной области. Это приводит к результату, что спад контролируетсяи не чувствителен к глубине перехода. Это существенно для технологии, так как на практике трудно масштабировать глубину перехода без деградации рабочего тока вследствие увеличения последовательного сопротивления. Но если возможно создание МОПТ с(например, используя процесс выращивания приподнятых (raised) областей cтока и истока, спад будет линейно уменьшаться пропорционально.

В то время как аналитические результаты, подобные (С1.27), дают нам ключ к пониманию ККЭ, вообще проектирование короткоканальных приборов проводится с помощью двумерного моделирования для получения более точных результатов.

С1.8. Короткоканальный подпороговый наклон и чувствительность к подложке

Член () в выражении (С1.26) ухудшает подпороговый размах короткоканального прибора, так как он уменьшает чувствительностьк изменениюи, следовательно, к изменению порогового напряжения. Другими словами,

(С1.29)

Следуя выражениям (3.1.6), (3.1.8), можно записать подпороговый размах короткоканального прибора как

(С1.30)

До тех пор, пока , существенная деградация подпорогового размаха по сравнению с длинноканальным значением отсутствует.

При наличии смещения подложки , можно заменитьинаи, и условие порогана. Короткоканальный спад, выражение (С1.27), тогда выражается как функция смещения подложки, по которой может быть вычислена чувствительность. После линеаризации приближенный результат

. (С1.30)

Заметим, что обратное смещение подложки усиливает короткоканальный спад. Комбинируя выражение (С1.30) с длинноканальной чувствительностью к подложке, выражение (3.3.3), мы получаем чувствительность к подложке короткоканального прибора при

, (С1.31)

которое слегка меньше длинноканального значения, . Это есть следствие того, что в короткоканальном приборе часть заряда обедненного слоя в подложке связана со стоком и истоком вместо затвора.

С1.9. Экстремально ретроградное легирование (Ground-Plane) МОПТ

Подобный же анализ можно выполнить для экстремально ретроградного профиля легирования вместо ранее предполагаемого однородного легирования. При таком профиле легирования толщина обедненного слоя равна нелегированной толщине слоя, независимо от напряжения затвора. Анализ проще, чем в случае однородного легирования, поскольку есть просто непрерывная линейная функциях для всей области . Он также более точен, поскольку полное нижнее граничное условиевдольBE на рис.С1.4 удовлетворяется без необходимости дляряда. Результат подобен выражению (С1.27) с параметром а, замененным на m/2. Так как в общем случае ,экстремально ретроградно легированные МОПТ имеют слегка лучший ККЭ, чем в случае однородного легирования для тех же самых и.

С1.10 Обобщенная длина масштабирования для high-k диэлектриков

Когда длина канала КМОПТ уменьшается до 20-30нм, толщина оксида до ≈1нм, возникает необходимость в контроле ККЭ. Туннельный ток затвора мог быть неприемлемо высоким для таких атомарно тонких оксидов. Проблема могла быть решена путем использования диэлектриков с высокой диэлектрической проницаемостью (high-k диэлектриков) в качестве подзатворных диэлектриков. Нормальное поле (в кремнии) и емкость затвора при использовании high-k диэлектрика с диэлектрической проницаемостью и толщиной

(С1.32)

таковые же, как при использовании окисного слоя с диэлектрической проницаемостью и толщиной. Если, физическая толщинаhigh-k диэлектрика много больше, чем, следовательно, значительно уменьшая туннельный ток (квантово-механическое туннелирование не имеет никакого отношения к диэлектрической константе материала). На практике довольно трудно разработать high-k диэлектрик для затвора с приемлемыми характеристиками для использования в КМОП приборах. High-k диэлектрики в настоящее время одни из наиболее исследуемых объектов в области СБИС.

Из модели длины масштабирования для одной области ожидается, что дляhigh-k диэлектриков. Однако это справедливо только для , когда преобладают нормальные (вертикальные) поля. Когда возрастают и, ис одинаковым коэффициентом, то есть при постоянной емкости, продольные поля становятся более важными, поскольку высокая диэлектрическая постоянная их не улучшает. При произвольных диэлектрической постоянной и толщине необходимо использовать обобщенную модель двух областей для длины масштабирования, описанную в Приложении 1. При согласовании граничных условий для нормальных и тангенциальных полей на границе кремний-диэлектрик, собственные значения длины масштабирования получаются из уравнения:

. (С1.33)

Это уравнение имеет бесконечное число решений с уменьшающейся степенью . Наименьшая степень собственного значения, или наименьшее, преобладает, так как короткоканальная компонента потенциала пропорциональна, как и в модели одной области. Уравнение (С1.33) не может быть решено аналитически. Численное решение для наибольшихпоказано в нормализованных единицах на рис.С1.6 для некоторых типичных значений.

Рис.С1.6. Численное решение уравнение (С1.33) для различных значений . Пунктирные линии в правом нижнем углу показывают поведение асимптотического решениядля[3].

Важность остается прежней: она предписывает минимальную длину канала,, как предсказывалось с модели одной области, обсуждавшейся выше.

На рис С1.6 наблюдаются следующие особенности решения уравнения (С1.33):

• , если больше, чем,.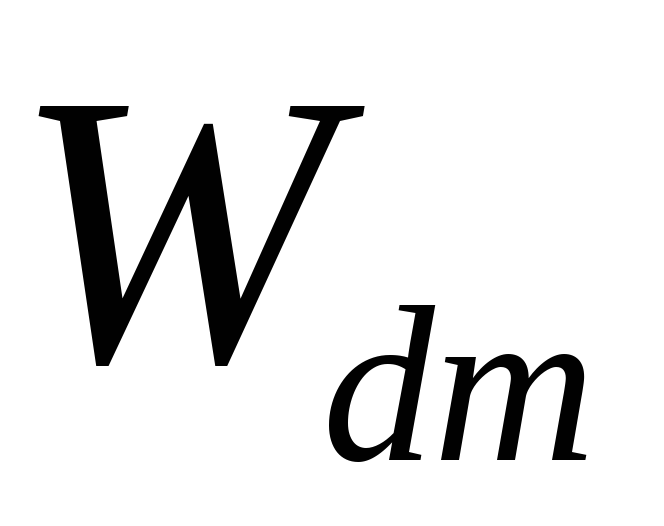

• в особом случае ,, физической высоте в боксе на рис. С4.1.

• в особом случае ,, независимо от.

• если (нижний правый угол на рис.3.26),. Это приближенное решение получается в модели одной области.

• если (верхний левый угол на рис.3.26),.

В то время как выражение (С1.33)и рис.С1.6. симметричны относительно и, анализилиm-фактора требуют, чтобы . Другими словами, дляприемлемо только решение в нижнем правом углу рис.С1.6.. В этой областиhigh-k диэлектрик помогает, так как , и для того же самогоболее высокоепозволяет большее отношение. Однако, вследствие чрезвычайной нелинейности кривой длярешение длябыстро отклоняется от выше рассмотренной модели одной области (линейная аппроксимация – пунктиры на рис.С1.6.), когдавозрастает. Существует пределили, где− физическая толщина изолятора независимо от того, как велика его диэлектрическая постоянная. Физически это обусловлено продольными полями, в отличие от вертикальных полей, не затрагиваемых диэлектрической константой материала. В приборах с очень толстым и с очень высокой диэлектрической константойhigh-k диэлектриком доминируют продольные поля, так что длина масштабирования определяется главным образом физической толщиной пленки.

Заметим, что для <1, то естьSiO₂, кривизна кривой на рис.С1.6. противоположна той, что при>1. Это значит, чтовсегда ниже (лучше), чем аппроксимация одной областью,, так какувеличивается.