16

Методические указания

к проведению практических занятий по дисциплине

«Физика наноразмерных полупроводниковых структур»

Семинар 2

С2. Метод трансформации и модель MASTAR

План семинара

С2.1.Основы метода трансформации (Voltage-Doping Transformation -VDT)

С2.2. Короткоканальный эффект (SCE)

С2.3. Индуцированное стоком понижение барьера (DIBL)

С2.4. Влияние глубины перехода

С2.5. Влияние ККЭ на подпороговый размах

С2.6. Правила «хорошего проектирования»

С2.7. Модель MASTAR

Литература

Задание на СРС

С2.1.Основы метода трансформации (Voltage-Doping Transformation - VDT)

Существует три главных короткоканальных эффекта. Первый эффект связан с уменьшением величины порогового напряжения с уменьшением длины канала (roll-off). Обозначим его ККЭ (SCE). Второй короткоканальный эффект связан с уменьшением высоты потенциального барьера между стоком и истоком при увеличении напряжения на стоке (DIBL). Третий эффект связан с увеличением подпорогового размаха (S) при уменьшении длины канала. Все эффекты связаны с нарушением приближения плавного канала и появлением двумерной картины электрического поля.

Метод Voltage-Doping Transformation (VDT) [1] позволяет любые 2D электростатические проблемы свести к 1D проблемам.

На рис.С2.1 в криволинейной ортогональной системе координат х, y представлено распределение линий поля (координата y) и линий потенциала (координата х) в МДПТ, находящемся в подпороговой области. Координата y измеряет расстояние вдоль данной линии поля и координата х измеряет расстояние вдоль данной линии , которая перпендикулярна линиям поля

a

b

Рис.С2.1 (a) Распределение потенциала вдоль у-линий в криволинейной системе координат; (b) компоновка линий поля у и перпендикулярных к ним линий эквипотенциалей х. Затемненная полоска – в окрестности виртуального катода – локальный минимум потенциала вдоль линий у.

и начинается на поверхности. Мы назовем осью х особую линию , которая соответствует минимуму распределения потенциала (виртуальный катод) в направлении y. Можно показать [1], что вблизи оси х (заштрихованная область на рис.С2.1) лапласиан в координатах ху принимает форму, обычную для декартовых координат ХУ, так что уравнение Пуассона можно записать в традиционном виде

В общем случае есть функция х и у, но на оси х (у = 0) – функция только х. Давайте предположим, что эта функция известна и равна . Тогда

, (С2.1)

где .

Последнее выражение – сущность метода VDT, который, как мы покажем, позволяет свести 2D уравнение Пуассона вдоль оси х к 1D в форме (С2.1). Физически (С2.1) означает, что влияние продольных линий поля исток-сток на высоту потенциального барьера может быть эквивалентно заменено на уменьшенную концентрацию примеси . Заметим, что отрицательное значение показывает, что все ионы примеси связаны полем стока, что просто означает, что МОПТ находится в состоянии прокола.

Любые 2D распределения потенциала в области, содержащей заряд с плотностью N_B эквивалентны 1D распределению потенциала в этой области, содержащей заряд с плотностью. Как мы покажем далее, это простое наблюдение может иметь большое практическое значение при условии, что мы способны рассчитать .Чтобы показать это, давайте рассмотрим МОПТ-структуру, показанную на рис.С2.1. Применительно к этой структуре метод VDT гарантирует, что потенциал вдоль данной вертикальной оси может быть рассчитан из 1D уравнения Пуассона, если заменить реальную концентрацию легирующей примеси N_B модифицированной (трансформированной) концентрацией . Так как 1D решение для потенциала в МОПТ-структуре хорошо известно, достаточно формально заменить N_B на в хорошо известных выражениях. Это означает, что обоснованность всех моделей (например, модели порогового напряжения), выводимая из 1D уравнения Пуассона для длинноканального транзистора, может быть распространена на короткоканальные транзисторы простой и формальной заменой реальной концентрации на трансформированную. Так как пороговое напряжение (и многие другие важные величины) короткоканального транзистора зависит от потенциала на так называемом виртуальном катоде (минимум потенциала, соответствующий максимуму высоты потенциального барьера между истоком и стоком в подпороговой области), необходимо определить трансформированную концентрацию вдоль вертикальной оси, проходящей через виртуальный катод, как показано на рис.С2.1. Все другие области транзисторной структуры здесь неважны, и, следовательно, метод VDT не стремится найти потенциал где-нибудь еще, кроме как вдоль виртуального катода.

В короткоканальном транзисторе геометрия распределения потенциала не декартова (прямоугольная), но, как показано в [1] лапласиан, соответствующий криволинейной системе координат на рис.С2.1, сводится к декартову лапласиану, когда рассматривается сокращенная область определения решения очень близко к окрестности виртуального катода (затемненная область на рис. С2.1).

Давайте предположим параболическое распределение потенциала в латеральном направлении (ось y), и определим параметры a,b,c из следующих граничных условий:

где − контактная разность потенциалов перехода исток (сток)-подложка, и − напряжения исток-подложка и сток-исток, соответственно L – длина линий поля, m – расстояние от истока до виртуального катода (ось х), измеренное вдоль данной линии . После некоторых преобразований это дает [предупреждение: так как становится новым решением (в сокращенной области), заменяя , мы используем для простоты то же самое обозначение ]:

(С2.2)

и, следовательно,

, (С2.3)

где .

Заметим, что вследствие криволинейной геометрии решения величина L не есть длина канала транзистора, а длина данной линии поля между истоком и стоком. В дальнейшем мы получим соотношение между L и длиной канала транзистора.

Все длинноканальные модели транзистора (1D), которые зависят от высоты потенциального барьера, остаются справедливыми также и для случая короткого канала (2D), если заменить в этих выражениях реальную концентрацию N_B на трансформированную .

Поэтому, давайте подставим трансформированную концентрацию в классическое уравнение для порогового напряжения:

(С2.4)

Полагая, что поправочный член , раскладываем выражение в ряд Тейлора и, ограничиваясь членами первого порядка, получаем:

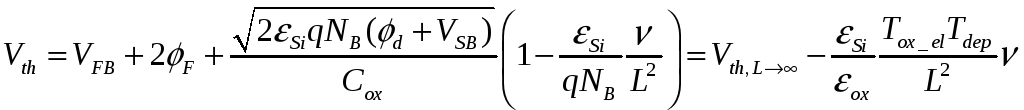(С2.5)

где

. (С2.6)

Полное выражение для слишком сложное:

(С2.7)

мы упростим его.

С2.2. Короткоканальный эффект (sce)

Давайте сначала рассмотрим случай .Так как для расчета порогового напряжения распределение потенциала близко к поверхности играет бòльшую роль, чем глубоко в объеме, мы предположим среднее значение потенциала вдоль оси у (выбор конкретного значения ¾ не критичен, много значений около ¾ дает хорошие результаты, но так как ¾ дополнительно приводит к значительному упрощению в выражении для , мы примем это конкретное значение). Это позволяет существенно упростить выражение для , которое сокращается до . Тогда может быть переписано следующим образом:

, (С2.8)

где

. (С2.9)

С2.3. Индуцированное стоком понижение барьера (DIBL)

Давайте теперь рассмотрим случай . Математическое рассмотрение этого вопроса подобно предыдущему. Предположим и малым относительно 3/4, тогда выражение для становится . В противоположность этому, если , выражение превращается в , которое по тем же самым причинам также хорошо аппроксимируется . Следовательно, каково бы ни было значение , величина корректно аппроксимируется формулой

.

Используя это значение в выражении (С2.5) для , мы получаем, как и в случае SCE:

. (С2.10)

Это можно переписать следующим образом:

, (С2.11)

где

. (С2.12)

С2.4. Влияние глубины перехода

Точный анализ геометрии электрических полей (путем моделирования) обнаруживает, что линии поля, соединяющие исток и сток довольно параллельны поверхности, и таким образом короче в случае глубокого перехода, чем в случае мелкого перехода. Только в случае бесконечно глубокого перехода длина пути¹ носителей от истока к стоку равна расстоянию L между переходами истока и стока. Во всех других случаях мы должны заменить L на во всех выражениях, в том числе и в результатах VDT, где учитывает кривизну линий поля, см рис. С2.4. Производя это в VDT-трансформированном выражении для порогового напряжения (С2.5), получаем:

(С2.13)

И, предполагая , мы можем упростить выражение

. (С2.14)

Рис.С2.4. Схематическое представление линий поля, проходящих от истока к стоку на глубине х для глубокого перехода – (а) и для мелкого перехода – (в). В последнем случае длина линий поля возрастает, следовательно, лучше противодействует SCE.

Точный расчет невозможен, но можно, используя граничные условия на рис С2.4, записать следующие аппроксимативные выражения:

.

Подставляя эти выражения для в (С2.14), мы разложим знаменатель в ряд Тейлора и, пренебрегая членом ,² получим:

(С2.15)

Наилучшее соответствие экспериментальным данным получается, если полагать , что дает в результате:

(С2.16)

или ,

где , (С2.17)

. (С2.18)

Константы 0,64 и 0,8 для SCE и DIBL – эмпирические коррекции, полученные в результате калибровки выражений (С2.17) и (С2.18) по отношению ко всем последующим поколениям технологии от 0,7мкм до 0,1мкм. Самые последние результаты исследований приборов длиной от 60нм до 20нм хорошо согласуются с этими выражениями.